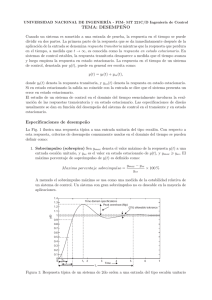
6) La expresión general de una función Lorentziana es la siguiente

6)
La expresión general de una función Lorentziana es la siguiente:
=
1
− + Pero ya hemos visto la transformada de Fourier de una cierta función:
ℱ || =
1
+ Entonces, invirtiendo la función, y teniendo en cuenta una propiedad ya
calculada:
ℱ
1
= 2 ||
− + 7)
Tenemos:
ℱ =
1 Entonces, la anchura media de ambas funciones es, respectivamente, ∆
y ∆/; entonces, la mínima indeterminación en la medida de ambas
funciones estará dada por:
∆ · ∆ = ·
1
=1
Ya que existe un punto en el que ambas están igual de extendidas.
Pero, en principio, no tiene por qué tener cota superior, ya que ∆ puede
estar arbitrariamente extendida; así, tenemos:
∆ · ∆ ≥ 1
8)
El polinomio característico de esta matriz es:
! − "# + 2$ #% & = 0
Para resolverlo, consideramos dos casos:
a) & = 0
Podemos obtener sencillamente los autovalores:
"=!
n veces
Lo que significa que la actuación de este operador consiste en multiplicar
por la energía cinética.
b) & = $
Tenemos
! − "# + 2$ # = 0
! − "# = −2$ #
Tomando raíces cuadradas a ambos lados:
! − " = √−2$
/
" = ! − √−2$
/
Entonces, los autovalores son reales puros o complejos, dependiendo del
valor de N.
Ahora hemos de resolver la ecuación
0
1 = 23 13
0$ Como es un sistema de EDO acopladas, para resolverlo intentaremos el
siguiente ansatz:
1 = 45
Entonces:
6 45 = 23 3 45
Que equivale al problema de autovalores:
2 = 6
Pero ya hemos visto cuáles son sus autovalores; ahora necesitamos
también hallar los autovectores . Valoramos los dos casos:
a) & = 0
0
9$
80
…
70
Tenemos:
6=!
%
$ 0 … 0
0
0 $ … …= 9 = 9 0 =
$ 0 $ …< 8 > < = 8 0 <
…
… … … …
…
… … $ 0 ; 7 #; 7 0 ;
= 0
% + > = 0
+ ? = 0
> + @ = 0
…
# + # = 0
#% = 0
Por tanto, hallamos que = 0 si A es par.
Ahora bien, sabemos que los autovalores de un operador hermítico son
todos reales, lo que implica que B ha de ser impar, según los autovalores
que hemos obtenido. B − 1 es par, así que no afecta a los demás, y
tomamos:
Y entonces: 1$ = D5
b) & = $
√−2$
9 $
8 0
…
7 $
/
1
0
9−1=
<
=8
80<
81<
…
7±1;
6 = ! − √−2$
/
$
√−2$
$
…
…
/
0
$
/
√−2$
…
…
…
…
$
…
$
%
$
0
… = 9 = 9 0 =
… < 8 > < = 8 0 <
…
…
…
/
√−2$; 7 # ; 7 0 ;
Entonces los satisfacen este sistema de ecuaciones.
Ahora tenemos que estudiar el espectro de este operador. Si tenemos un
sistema cuántico, se cumple:
2 = AℏF
−A6/ℏ = −AG/ℏ
Entonces, para & = 0:
6=G
G=!
La energía G toma los valores de !, variable que podría ser discreta o
continua, ya que no hemos hecho ningún supuesto al respecto. No
obstante, todos los niveles tienen el mismo autovalor, por lo que el
espectro sería una simple franja.
Para & = $:
G = ! − √−2$
/
Ahora bien, si hacemos B → ∞, hay poca separación entre raíces, por lo
que el espectro se puede tratar como continuo.
Daniel E. Borrajo Gutiérrez