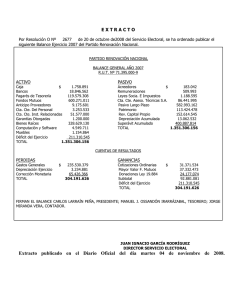
v = lim Derivada: v = lim x t ≡ dx dt Velocidad instantánea: v = dx dt

∆x
∆t→0 ∆t
v = lim
Derivada:
dx
∆x
≡
∆t→0 ∆t
dt
v = lim
Velocidad instantánea:
v=
dx
dt
Velocidadinstantánea
pendienteen un punto
tangente en un punto
derivada de x respecto de t
variación de x respecto de t
Vector velocidad (instantánea):
v=
dx
i
dt
Ejemplo: x(t) = 5t2
Reglas sencillas para derivar
d
(cte) = 0
dt
Ej:
d
(2)
dt
= 0,
dc
dt
= 0.
Función x = t
dx
dt
=
=1
dt
dt
Linealidad
d
d
d
(x1 + x2 ) = ( x1 + x2 )
dt
dt
dt
Derivada de un producto
d
d
d
(x1 × x2 ) = ( x1 )x2 + x1 ( x2 )
dt
dt
dt
Ej:
d 2
(t )
dt
= dtd (t × t) = 2t dt
= 2t
dt
Función potencial general:
d n
t = ntn−1
dt
Si n = 1: se verifica que
d
t
dt
= 1t1−1 = 1t0 = 1
Aceleración
1
Cambio de la velocidad con el tiempo:
v = v(t) =⇒ ∃ a
Aceleración media
am =
Dimensiones: [a] = [v]
= ms 1s =
[t]
Aceleración instantánea
∆v
∆t
m
s2
∆v
∆t→0 ∆t
a = lim
(pendiente de la tg a la curva de v(t) en t)
Derivada
dv
a=
dt
Derivada segunda
dv
d dx
d2 x
a=
=
= 2
dt
dt dt
dt
Por lo tanto:
d2 x
a= 2
dt
Aceleración cero:
dv
⇒ v = cte. (MRU)
a=0=
dt
Velocidad cte.
v = cte. ⇒
dv
=0⇒a=0
dt
v = cte. ⇔ a = 0
v = cte. ⇒ pendiente = cte.
x(t) = vo t + xo
Si a = cte. ⇒
v(t) = vo + at
2
De la figura:
1
vm = (vo + v)
2
Por lo tanto:
Pero
1
∆x = vm t = (vo + v)t
2
1
v = vo + at ⇒ ∆x = (vo + vo + at)t
2
1
∆x = (2vo t + at2 )
2
O sea:
1
x = xo + vo t + at2
2
Por otro lado:
v = vo + at ⇒ t =
v − vo
a
1
x = xo + vo t + at2 =
2
1 v − vo 2
v − vo
= xo + vo
+ a
a
2
a
v2 = vo2 + 2a∆x
Resumen de ecuaciones: si xo = 0
1
x = vo t + at2
2
v = vo + at
v 2 = vo2 + 2ax
Extras:
1
(vo + v)
2
1
x =
(vo + v)t
2
vm =
siempre que a = cte. (MRUA)
1
Movimiento relativo
Conceptos previos
• movimiento
• desplazamiento
• intervalo
• sistema de coordenadas
3
• velocidad
• aceleración
• pendiente
• velocidad instantánea
• “derivada”
4
Hipótesis galileanas (de Galileo) de velocidad relativa:
5