NUMEROS DECIMALES Archivo

5
Los números decimales
Presentación de la unidad
Conocimientos mínimos
•La ampliación del campo numérico de los números enteros a los
decimales no es obvia y exige la elaboración de una compleja
estructura de conceptos y nuevas relaciones. La prueba de esta
dificultad está, históricamente, en su tardía aparición. De hecho,
la primera vez que se tiene constancia de la presencia de los números decimales es en el libro De Thiende (la decena), del matemático holandés Simon Stevin (1548 - 1620). Para expresar 0,548
escribía: 5 1 4 2 8 3. De esta manera, lo que para nosotros serían
5 décimas, 4 centésimas y 8 milésimas, para él eran 5 primeras, 4
segundas y 8 terceras.
•A lo largo de la unidad profundizaremos en la estructura del sistema de numeración decimal (órdenes de unidades decimales) y
revisaremos los algoritmos para las distintas operaciones con números decimales. Pondremos especial atención en los procedimientos para dividir decimales y para aproximar el cociente al
orden de unidades deseado, habida cuenta de los errores que
suelen cometer los alumnos y alumnas en esta operación.
•La calculadora sencilla de cuatro operaciones puede resultar una
buena herramienta para facilitar la investigación y el descubrimiento de relaciones y propiedades.
Para que los números decimales resulten de utilidad en el análisis,
interpretación y representación del entorno, consideramos imprescindibles los siguientes contenidos de la unidad:
•Leer y escribir números decimales.
•Conocer y utilizar las equivalencias entre los distintos órdenes de
unidades.
•Ordenar números decimales.
•Aproximar un número decimal a un determinado orden de unidades.
•Calcular por escrito con números decimales (las cuatro operaciones).
•Realizar sencillas operaciones y estimaciones mentalmente.
•Utilizar la calculadora para operar con números decimales.
•Elaborar e interpretar mensajes con informaciones cuantificadas
mediante números decimales.
•Resolver problemas cotidianos en los que aparezcan operaciones con números decimales.
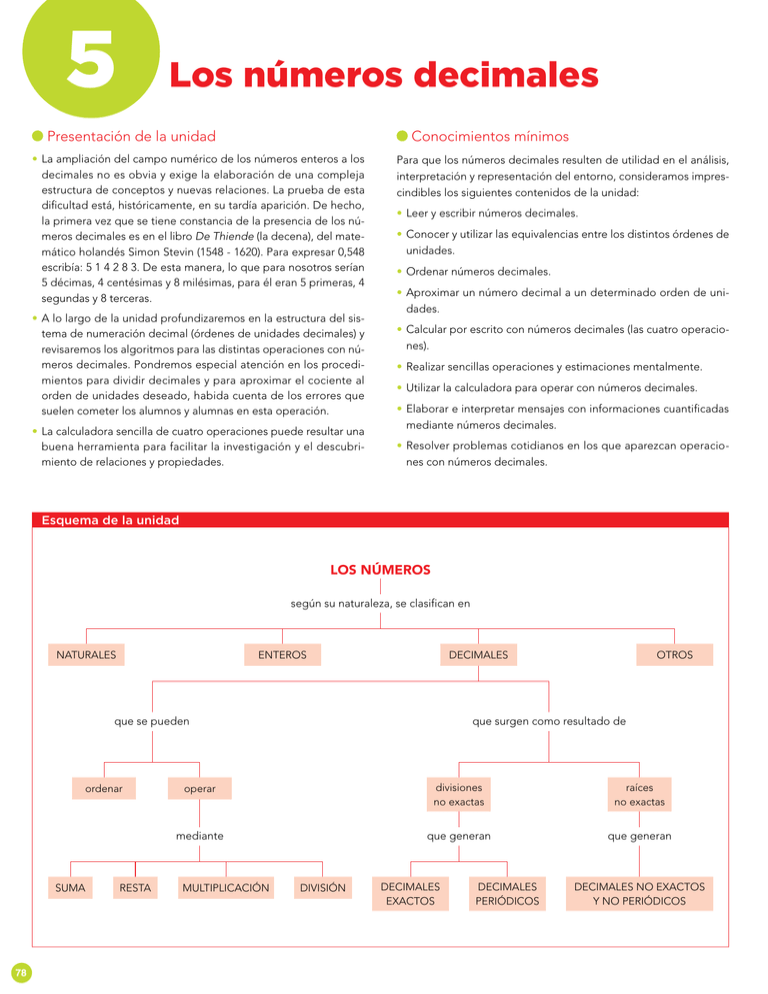
Esquema de la unidad
LOS NÚMEROS
según su naturaleza, se clasifican en
NATURALES
ENTEROS
DECIMALES
que se pueden
ordenar
SUMA
78
RESTA
OTROS
que surgen como resultado de
operar
divisiones
no exactas
raíces
no exactas
mediante
que generan
que generan
MULTIPLICACIÓN
DIVISIÓN
DECIMALES
EXACTOS
DECIMALES
PERIÓDICOS
DECIMALES NO EXACTOS
Y NO PERIÓDICOS
Anticipación de tareas
La lectura inicial servirá para ejercitar la comprensión lectora y para
mostrar los dos aspectos que justifican el estudio de las matemáticas: el práctico y el intelectual.
•Recordar la estructura del S.N.D.
•Revisar las propiedades y los algoritmos de las operaciones con
números naturales.
•Recordar la prioridad de operaciones en las expresiones con paréntesis y operaciones combinadas de números naturales.
•Practicar y asegurar el cálculo mental.
•Recordar el orden de los números naturales y su representación
en la recta numérica.
Adaptación curricular
En la parte de “Recursos fotocopiables” se ofrece una adaptación
curricular de esta unidad 5 del libro del alumnado, para cuya elaboración se han tenido en cuenta los conocimientos mínimos que
aquí se proponen.
Los contenidos, si se adaptan a esos mínimos exigibles, o bien no
han sufrido cambio alguno o bien se han modificado ligeramente
para adecuarlos al posible nivel de los estudiantes a quienes va
dirigido. Lo mismo cabe decir de los ejercicios prácticos que se
proponen.
Si algún contenido supera los mínimos exigibles, o bien se ha suprimido o bien se ha adaptado para ajustarlo a los requisitos exigidos.
Finalmente, los ejercicios y problemas con los que finaliza la unidad se han reducido en cantidad y se han modificado o bajado de
nivel hasta adaptarse a lo convenido.
Lo mismo cabe decir de la autoevaluación.
En la siguiente tabla se recoge una relación de actividades para atender y trabajar el aprendizaje cooperativo, el pensamiento comprensivo, el pensamiento crítico, la interdisciplinariedad, las TIC, el emprendimiento y la resolución de problemas. Unas están propuestas en el libro del alumnado (L.A.), y aquí se hace referencia a ellas indicando la página y la
actividad y otras, como se indica, se sugieren en esta Propuesta Didáctica (P.D.).
Una selección de estas sugerencias están marcadas en el libro del alumnado con un icono; aquí se han marcado con (*).
APRENDIZAJE COOPERATIVO
PENSAMIENTO COMPRENSIVO
PENSAMIENTO CRÍTICO
Pág. 87. Actividad sugerida en esta P.D. (*)
Pág. 89. Actividad 6
Pág. 93. Actividad 9 (*)
Pág. 93. Actividad sugerida en esta P.D.
Pág. 91. Ejercicio resuelto
Pág. 98. Actividad 10
Pág. 94. Problemas resueltos
Pág. 99. Actividades 23, 24
Pág. 98. Actividad 6
Pág. 99. Actividad 25
Pág. 99. Actividad 26 (*)
Pág. 99. Actividades 29 y 31
INTERDISCIPLINARIEDAD
Pág. 86. Actividad sugerida
en esta P.D. (*)
TIC
EMPRENDIMIENTO
Pág. 86. Actividad suge- Pág. 90. Actividad 12
rida en esta P.D. (*)
Pág. 100. Actividades
36 (*), 37 y 38
RESOLUCIÓN DE PROBLEMAS
Todos los problemas propuestos en el L.A. están encuadrados en este apartado. Aquí se señalan algunos que tienen especial interés.
Pág. 101. Actividades 49 (*) y 51 (*)
Pág. 96. Actividad 15
Pág. 102. Actividad “Investiga y
exprésate” (*)
Pág. 100. Actividad “Aprende a resolver problemas” (*)
Pág. 101. Actividades 46, 50, 52
Pág. 103. Actividad “Entrénate resolviendo problemas” (*)
79
5
Los números decimales
Medida de unidades incompletas
Medimos el lapicero con la regla:
La mayor parte de los sistemas de numeración de las antiguas civilizaciones son de base decimal, que proviene, sin duda, de contar con los dedos
de las manos.
1
¿Cuál o cuáles de estas medidas son correctas?:
127 mm
12,7 cm
1,27 dm
0,127 m
Números y partes de kilo
La balanza digital marca el peso de la sandía:
3,000 kilos.
2
¿Qué número marcará la balanza digital si pesas media sandía?
3
¿Qué marcará si pesas una botella de refresco? ¿Y si pesas un bote de miel?
¿Y si pesas un bote de tomate?
L
os indios, en el siglo VII, añadieron a la base decimal la
notación posicional: el valor de un signo (cifra), depende
de la posición que ocupa. Este grandioso avance vino unido
a la invención del cero para ocupar las posiciones vacías.
Ofertas en el supermercado
Marta va al supermercado.
—¡Tráeme un paquete de lentejas! —le encarga su vecina Rosa.
—¡Y a mí, uno de garbanzos! —le pide su vecino Germán.
Ya en la tienda, adquiere estos dos lotes:
4€
E
l sistema de numeración decimal-posicional se usó inicialmente en Europa solo para designar números enteros. Fue en el siglo XVI cuando se hizo extensivo, también,
para cuantificar partes de la unidad (números decimales).
Al iniciar la unidad
• La lectura sirve de introducción a la unidad, anunciando los contenidos
que se van a trabajar y haciendo un breve repaso a la evolución histórica
de los números hasta la aparición de los decimales.
• Tiene interés que los estudiantes aprecien la importancia de la aparición del cero, y constaten que se trata de un elemento imprescindible
para el desarrollo de nuestro sistema de numeración decimal.
Efectivamente, el cero permite colocar una cifra en el orden de unidades deseado, base de la estructura de un sistema de numeración de tipo posicional. Como muestra, basta pedirles que observen y comparen,
por ejemplo, los números ocho, ochenta y ochocientos en escritura
egipcia y en escritura decimal, y reflexionen sobre la necesidad del cero
en cada una.
Cuestiones para detectar ideas previas
• Se sugiere la lectura colectiva de las actividades y su resolución en gran
grupo, poniendo en común opiniones e ideas.
• La primera actividad detecta si los estudiantes interpretan correctamente la recta numérica y hasta qué punto controlan las equivalencias entre
distintos órdenes de unidades. La segunda atiende al razonamiento lógico y a operaciones básicas, mediante cálculo mental, con resultado
decimal. La tercera incide en la aproximación por redondeo.
• Como complemento, se sugieren actividades como las que siguen:
– Una lechuga cuesta 0,55 €. ¿Cuánto cuestan 2, 3, 4… lechugas?
– ¿A cómo sale el kilo de dátiles si un cuarto de kilo cuesta 2,30 €?
¿Cuánto deberá cobrar a Rosa por el paquete de lentejas y a Germán por el de garbanzos?
Interdisciplinariedad
Se sugiere la siguiente actividad: Describe una situación en la que los números decimales resultan útiles para: la economía doméstica, la dietética,
el deporte y la industria farmacéutica.
TIC
Se sugiere la siguiente actividad: Busca en Internet:
a)¿Qué matemáticos fueron los primeros en utilizar la coma para los números decimales? ¿Cuándo fue?
b)Infórmate de la curiosa forma que utilizaba Simon Stévin para expresar
los números decimales, y escribe en esa notación el número 18,395.
Aprendizaje cooperativo
Se sugiere, para enfocar estas actividades hacia el aprendizaje cooperativo, lo siguiente: Los estudiantes, en pequeño grupo, comentan y resuelven las actividades. Después, en gran grupo, contrastan opiniones y
acuerdan conclusiones.
Soluciones de las actividades
1 Todas las medidas son correctas: expresan la misma longitud en distintas unidades.
2 1,5 kilos
– ¿Cuál es la diferencia de precio entre un kilo de naranjas de mesa, a
2,75 €/kg, y un kilo de naranjas de zumo, a 1,95 €/kg?
3 Al pesar una botella de refresco marcará 1,5 kilos. Al pesar un bote de
– ¿Cuánto fresón puedes comprar con 3 euros si el kilo está a 1,50 €?
4 Por el paquete de lentejas deberá cobrar a Rosa 1,33 euros, y a
– Elabora una lista de compra con un coste total de 10 euros.
80
4
5€
miel marcará 0,75 kilos. Al pesar un bote de tomate marcará 0,5 kilos.
Germán, por el de garbanzos, 1,67 euros.
1
5
UNIDAD
Estructura de los números decimales
Ten en cuenta
Los órdenes de unidades decimales
1 DÉCIMA
Para expresar cantidades más pequeñas que la unidad, utilizamos los órdenes de
unidades decimales.
• Al dividir una unidad en diez partes iguales, cada parte es una décima.
1 UNIDAD
5,3
5
1
0,1 = —
10
5,4
Orden en los números decimales
5,5
6
Los números decimales quedan ordenados en la recta numérica.
Los ceros a la derecha de un número decimal no modifican el valor del
número.
U,
d
2,
5
2,
5
0
2,
5
0
c
–2
m
5,36
5,4
5,5
5,36
1000 MILÉSIMAS
5,365
5,37
c
m
3
7
5
6,
1
0
0
3,25
3,4
↓
↓
3,25 < 3,40 → porque 25 c < 40 c
Piensa y practica
1. Escribe con cifras.
6. Observa la tabla
a) Ocho décimas.
b) Dos centésimas.
c) Tres milésimas.
d) Trece milésimas.
• En el sistema de numeración decimal, una unidad de cualquier orden se
divide en diez unidades del orden inmediato inferior.
2. Escribe cómo se leen.
10 U = 10 d = 100 c = 1 000 m = …
décimas
centésimas
milésimas
diezmilésimas
cienmilésimas
millonésimas
2
unidades
decenas
0,3
…
0,04
D
U,
d
c
m dm cm mm …
1
3,
0
5
7
4
Trece unidades y quinientas setenta
y cuatro diezmilésimas
Dos unidades y treinta
y cuatro centésimas
• Para leer un número decimal:
— Se nombra la parte entera expresada en unidades.
En la web
d
5,
5,365 → Cinco unidades y trescientas sesenta y cinco milésimas
2,34 €
↓
Practica la lectura de números decimales.
U,
5,375 < 6,1 → porque 5 U < 6 U
Por ejemplo:
• Al dividir una centésima en diez partes iguales, cada parte es una milésima.
1
0,001 = —
1000
Por ejemplo:
• Si tienen la misma parte entera, se iguala la cantidad de cifras decimales poniendo ceros a la derecha y se compara la parte decimal.
5,36 → Cinco unidades y treinta y seis centésimas
1 MILÉSIMA
100 CENTÉSIMAS
5,3
5
— Se nombra la parte decimal expresada en el orden de unidades de la cifra
decimal que queda a la derecha.
3
2
• Para comparar dos números decimales, se compara la parte entera.
2,5 = 2,50 = 2,500
1
0,01 = —
100
1
Pero también puedes comparar números sin acudir a la representación en la recta, observando las cifras y el lugar que ocupan:
0
• Al dividir una décima en diez partes iguales, cada parte es una centésima.
10 DÉCIMAS
0
–1
2,5
1,7
0,4
–1,7 < –0,5 < 0,4 < 1,7 < 2,5
5,3 → Cinco unidades y tres décimas
1 CENTÉSIMA
–0,5
–1,7
a) 1,2
b) 12,56
c) 5,184
d) 1,06
e) 5,004
f ) 2,018
3. Escribe con cifras.
U,
d
c
3,
2
5
3,
4
0
U,
d
y contesta.
m
c
m
4
0
2
0
0
3
0
0
0
a) ¿Cuántas centésimas hay en 40 milésimas?
b) ¿Cuántas centésimas hacen 200 diezmilésimas?
c) ¿Cuántas millonésimas hay en 3 milésimas?
7. Indica el valor que representa cada letra:
a) Once unidades y quince centésimas.
b) Ocho unidades y ocho centésimas.
3
A
B
4
c) Una unidad y trescientas once milésimas.
d) Cinco unidades y catorce milésimas.
6,2
N
M
D
C
P
Q
6,4
4. Escribe cómo se leen.
a) 0,0007
b) 0,0042
c) 0,0583
d) 0,00008
e) 0,00046
f ) 0,00853
g) 0,000001
h) 0,000055
i) 0,000856
5. Escribe con cifras.
1,56
Y
X
Z
1,57
8. Ordena de menor a mayor.
a) Quince diezmilésimas.
a) 5,83
b) 0,1
c) 0,5
b) Ciento ochenta y tres cienmilésimas.
c) Cincuenta y ocho millonésimas.
5,51
0,09
– 0,8
5,09
0,099
– 0,2
5,511
0,12
1,03
5,47
0,029
–1,1
88
Sugerencias
• Para comenzar, se sugiere recurrir a la interpretación y a la elaboración
de mensajes propios del lenguaje habitual que incluyan conceptos relativos a los números decimales:
89
Soluciones de “Piensa y practica”
1 a)0,8
b)0,02
c) 0,003
d)0,013
2 a)Una unidad y dos décimas.
– Me he puesto el termómetro y tengo tres décimas de fiebre.
b)Doce unidades y cincuenta y seis centésimas.
– Un gramo es la milésima parte de un kilo.
c) Cinco unidades y ciento ochenta y cuatro milésimas.
– La luz tarda en encenderse menos de una millonésima de segundo.
d)Una unidad y seis centésimas.
• Partiendo de la unidad representada en la recta numérica y, mediante
sucesivas particiones, vamos obteniendo y visualizando las décimas, las
centésimas, etc.
• La comprensión y la interpretación correcta de la recta numérica tiene importancia tanto desde el punto de vista práctico como desde el teórico:
e)Cinco unidades y cuatro milésimas.
f ) Dos unidades y dieciocho milésimas.
3 a)11,15
b)8,08
c) 1,311
b)Cuarenta y dos diezmilésimas.
– Desde el punto de vista teórico, ofrece apoyos visuales para relacionar los distintos órdenes de unidades y establecer sus equivalencias,
para ordenar números decimales, para realizar aproximaciones, etc.
f ) Ochocientas cincuenta y tres cienmilésimas.
• Para comparar, los estudiantes suelen encontrar dificultades cuando los
números tienen distinta cantidad de cifras decimales. Se recomienda
entonces que las igualen añadiendo ceros a la derecha.
Refuerzo y Ampliación
Recomendamos, del cuaderno n.º 1 de EJERCICIOS DE MATEMÁTICAS:
Refuerzo: Ejercicios del 1 al 6 de la pág. 3. Ejercicios del 1 al 8 de las págs.
18 y 19.
d)5,014
4 a)Siete diezmilésimas.
– Desde el punto de vista práctico, es la llave para la utilización de ciertos procedimientos relativos a otros campos de las matemáticas: lectura de mediciones, valoración de escalas, manejo de los ejes de
coordenadas, interpretación de gráficas estadísticas…
• Los estudiantes deben comprender que todo número decimal tiene su
lugar en la recta numérica, lo que implica la ordenación del conjunto de
los números decimales.
T
c) Quinientas ochenta y tres diezmilésimas.
d)Ocho cienmilésimas.
e)Cuarenta y seis cienmilésimas.
g)Una millonésima.
h)Cincuenta y cinco millonésimas.
i ) Ochocientas cincuenta y seis millonésimas.
5 a)0,0015
b)0,00183
c) 0,000058
6 a)
4b)
2c)
3 000
7 A = 3,5
B = 4,8
C = 5,9
D = 7,1
M = 6,22
N = 6,3
P = 6,35
Q = 6,42
X = 1,561
Y = 1,565
Z = 1,569
T = 1,571
8 a)5,09 < 5,47 < 5,51 < 5,511 < 5,83
b)0,029 < 0,09 < 0,099 < 0,1 < 0,12
c) –1,1 < –0,8 < –0,2 < 0,5 < 1,03
81
UNIDAD
Ten en cuenta
Los números decimales se pueden clasificar en tres grupos:
— Exactos: Con un número finito
de cifras.
2,75
— Periódicos: Con infinitas cifras
que se repiten.
#
41:11 = 3,727272… = 3, 72
— Otros: Con infinitas cifras que no
se repiten.
3 = 1,7320508…
Aproximación por redondeo
• Elijamos dos números cualesquiera; por ejemplo, 2,3 y 2,6. Es evidente que
entre ellos hay otros decimales:
En algunas ocasiones se nos presentan números con demasiadas cifras decimales
y preferimos, o nos vemos obligados, a sustituirlos por otros más manejables de
valor aproximado.
2,3 < 2,4 < 2,5 < 2,6
Ejemplo
• Busquemos, ahora, un número decimal comprendido entre 2,3 y 2,4.
En el banco me han calculado los intereses de dos cuentas bancarias:
Estos dos números se diferencian en una décima, y esa décima se puede dividir
en diez centésimas.
2,3
2,35
2,32
2,38
A → 18,2733 €
A → 18,27 €
La unidad monetaria más pequeña es el céntimo. Por eso, los resultados con muchas cifras decimales se han de concretar con redondeos a los céntimos.
2,3 = 2,30 < 2,32 < 2,35 < 2,38 < 2,40 = 2,4
• En el primer caso, cuenta A, la cantidad 18,2733 está más cerca de 18,27 que
de 18,28. Por eso se toman 27 céntimos (observa que la cifra de las centésimas
no cambia).
El proceso puede continuar indefinidamente o repetirse para cualquier otro par
de números.
Lola tiene una báscula en el cuarto de aseo que aprecia hasta las décimas de
kilo. Si el peso no coincide con un número exacto de décimas, parpadea entre la décima anterior y la siguiente. ¿Qué peso te atribuirías si la báscula
parpadeara entre 53,6 kg y 53,7 kg?
18,27
Observa
En las transacciones bancarias y comerciales, se aplican los redondeos
considerando que los que van a la baja
se compensan con los que van al alza.
Intercalamos un número decimal que ocupe la posición intermedia ente 53,6
y 53,7:
35,36
0,4 <
< 0,5
1,25 <
<8
0,3 <
< 0,5
< 1,27
3,42 <
< 3,43
10. Intercala un número decimal entre cada par de nú-
meros:
a) 2,99 y 3
b) 4 y 4,1
c) 3,1 y 3,11
d) 0,5 y 0,51
e) 0,523 y 0,524
f ) 1,999 y 2
11. Escribe, en cada caso, un número decimal que esté a
la misma distancia de los dos números dados:
a) 4 y 5
b) 1,8 y 1,9
c) 2,04 y 2,05
35,3682
35,37
Para redondear un número a un determinado orden de unidades:
• Se suprimen todas las cifras a la derecha de dicho orden.
• Si la primera cifra suprimida es igual o mayor que cinco, se suma uno a la
cifra anterior. Y si no lo es, se deja como está.
Piensa y practica
7<
18,28
Como ves, en cada caso se toma el céntimo completo más cercano.
Solución: Podemos decir que el peso asciende a 53,65 kilos, aproximadamente.
< 2,8
18,2733
• En el segundo caso, cuenta B, la cantidad 35,3682 está más cerca de 35,37 que
de 35,36. Ahora se toman 37 céntimos (observa que se ha sumado uno a la
cifra de las centésimas).
53,6 = 53,60 → 53,65 ← 53,70 = 53,7
casilla.
B → 35,37 €
¿Por qué las cantidades aplicadas no coinciden con las que se habían calculado?
Añadiendo alguna de esas centésimas a 2,3, obtenemos decimales comprendidos entre 2,3 y 2,4.
9. Copia en tu cuaderno y escribe un número en cada
B → 35,3682 €
Sin embargo, las cantidades ingresadas han sido:
2,4
Problema resuelto
2,6 <
Ejercicio resuelto
12. En un encuentro internacional de atletismo se dispu-
Aproxima a los gramos el peso de cada caja. Recuerda que un gramo es una
milésima de kilo.
ta la prueba de los 100 metros lisos.
Dos jueces se encargan de tomar el tiempo del ganador, pero obtienen una ligera diferencia en sus mediciones:
• Juez A → 9 segundos y 92 centésimas
• Juez B → 9 segundos y 93 centésimas
¿Qué tiempo le asignarías al ganador de la prueba?
13. Intercala, a intervalos iguales, tres números entre 2,7
y 2,8.
4 : 3 = 1,333333…
Cada caja pesa 1,333 kg.
5 : 3 = 1,666666…
Cada caja pesa 1,667 kg.
Piensa y practica
14. Redondea a las décimas.
15. Redondea a las centésimas.
2,7
2,8
a) 6,27
b) 3,84
c) 2,99
a) 0,574
b) 1,278
c) 5,099
2,700
2,800
d) 0,094
e) 0,341
f ) 0,856
d) 3,0051
e) 8,0417
f ) 2,99
90
Sugerencias
• Profundizando en la comparación y ordenación de números decimales,
y también con el apoyo de la recta numérica, se verá que entre dos decimales dados, por próximos que estén, siempre se puede colocar un
tercer decimal.
• Cuando los alumnos y las alumnas encuentren dificultades para intercalar un decimal entre otros dos que se diferencian solo en una unidad del
último orden (por ejemplo, 2,345 y 2,346), conviene mostrarles que la
dificultad se resuelve añadiendo un cero más a la derecha (2,3450;
2,3460).
Estos procedimientos implican reflexiones que ayudan a profundizar en
la estructura de los números y van abriendo camino para aprendizajes
futuros, como por ejemplo el cálculo infinitesimal.
• El redondeo es una actividad habitual que los estudiantes deben comprender y realizar con soltura. Se puede comenzar recordando los redondeos realizados anteriormente con números enteros y pasar, después, a redondeos de números decimales que aparecen de forma
natural en el quehacer diario:
– Mediciones con la cinta métrica: redondeo a los metros o a los decímetros.
– Mediciones con la regla: redondeo a los centímetros.
– Manejo de dinero: redondeo al euro y al céntimo.
• Continuamos la secuencia didáctica, con el apoyo de la recta numérica,
realizando redondeos a las unidades. Dominados estos, propondremos
redondeos a las décimas, después a las centésimas, etc.
• Podemos finalizar con una actividad a la que se enfrentarán frecuentemente el alumnado: redondear resultados obtenidos en la calculadora.
Haremos ver que la máquina ofrece con frecuencia resultados con demasiadas cifras decimales y que, en cada caso, debemos tomar la aproximación adecuada. Por ejemplo, cuando se trabaja con cantidades de dinero,
los resultados deben redondearse a las centésimas (céntimos de euro).
82
5
Entre dos decimales siempre hay otros decimales
91
Refuerzo y Ampliación
Recomendamos, del cuaderno n.º 3 de EJERCICIOS DE MATEMÁTICAS:
Refuerzo: Ejercicios del 1 al 6 de la pág. 3.
Soluciones de “Piensa y practica”
9 Por ejemplo:
2,6 < 2,7 < 2,8
7 < 7,5 < 8
0,3 < 0,4 < 0,5
0,4 < 0,45 < 0,5
1,25 < 1,26 < 1,27
3,42 < 3,425 < 3,43
a)2,995
b)4,05
c) 3,105
d) 0,505
e) 0,5235
f ) 1,9995
b)1,85
c) 2,045
10 Por ejemplo:
11 a)4,5
12 9 segundos y 925 milésimas
13 2,725; 2,750 y 2,775
14 a)
6,3b)
3,8c)
3,0d)
0,1 e)
0,3f )
0,9
15 a)
0,57b)
1,28c)
5,10d)
3,01 e)
8,04f )
3,00
ANOTACIONES
2
5
UNIDAD
Suma, resta y multiplicación de números decimales
Multiplicación por 10, 100, 1
000, …
Recuerda que para multiplicar un número decimal por 10, por 100, por 1 000,
…, solo hay que mover la coma hacia la derecha uno, dos, tres, … lugares.
Ya conoces la suma, la resta y la multiplicación de decimales. Por eso, nos limitaremos a repasarlas incorporando el manejo de los números negativos.
Suma y resta
Problema resuelto
En el depósito de frío de una granja, que estaba vacío, han vertido dos cántaras de leche, con 12,35 litros y 7,65 litros. Después, se han extraído dos
bidones para hacer queso, uno de 8,9 litros y otro de 5,45 litros. ¿Cuántos
litros quedan en el depósito?
entran
salen
12,35
8,9
+ 7,65
+ 5,45
20,00
14,35
12,35 l
7,65 l
8,9 l
5,45 l
¿? l
quedan
20,00
(12,35 + 7,65) – (8,9 + 5,45) = 20 – 14,35 = 5,65
– 14,35
5,65
Solución: En el depósito quedan 5,65 litros de leche.
En la web
Practica sumando números decimales.
Para sumar o restar números decimales:
• Se colocan en columna haciendo corresponder las comas.
• Se suman (o se restan) unidades con unidades, décimas con décimas, etc.
En la web
Practica restando números decimales.
Todo lo que se dijo sobre los números negativos en las operaciones con enteros
sirve también para las operaciones con decimales.
Multiplicación
Problema resuelto
Ejemplo
PIAS
CO
FOTO
unidad
,04 €
......... 0
idad
10 .........
25 € un
De 1 a
.... 0,0
...
...
ad
...
100
€ unid
0,019
De 11 a
............
0
10
Más de
• Coste de 1 000 fotocopias → 0,019 · 1 000 = 19,00 €
Para multiplicar un número decimal por la unidad seguida de ceros, se desplaza la coma hacia la derecha tantos lugares como ceros acompañan a la unidad.
Piensa y practica
1. Calcula mentalmente.
7. Calcula en tu cuaderno.
a) 0,8 + 0,4
b) 1 – 0,3
a) 3,25 · 16
b) 2,6 · 5,8
c) 27,5 · 10,4
c) 1,2 + 1,8
d) 2,4 – 0,6
d) 3,70 · 1,20
e) 4,03 · 2,7
f ) 5,14 · 0,08
e) 3,25 + 1,75
f ) 2,5 – 0,75
8. Opera como en el ejemplo.
2. Recuerda las operaciones con números positivos y ne-
• 5,6 – 2,1 · (0,5 – 1,2) = 5,6 – 2,1 · (–0,7) =
gativos y calcula mentalmente.
= 5,6 + 1,47 = 7,07
a) 0,5 – 0,75
b) 1,2 – 1,5
c) 0,25 – 1
d) 2 – 1,95
e) 0,4 + 0,8 – 1,6
f ) 2,7 – 0,95 – 1,04
a) 8,3 + 0,5 · (3 – 4,2)
9.
¿Verdadero o falso?
a) Al multiplicar un número por 0,8, aumenta su valor.
a) 3,25 - 4 - 4,75 - 5,5 - …
b) El resultado de multiplicar un número por 1,1 es
mayor que el número original.
b) 8,65 - 8,5 - 8,35 - 8,2 - …
c) 1,5 - 1,62 - 1,74 - 1,86 - …
c) Para multiplicar por 100, se desplaza la coma dos
lugares a la derecha.
4. Resuelve en tu cuaderno.
c) 12,4 – 18,365 + 7,62
b) 3,5 – 0,2 · (2,6 – 1,8)
c) (5,2 – 6,8) · (3,6 – 4,1) d) (1,5 – 2,25) · (3,6 – 2,8)
3. Añade tres términos a estas series:
3, 2 5 ← 2 cifras decimales
× 2, 5 ← 1 cifra decimal
1 6 2 5
⏐
6 5 0
↓
8, 1 2 5 ← 2 + 1 = 3 cifras decimales
redondeo
Solución: 8,125 € ⎯⎯⎯⎯→ 8,13 € pagaremos por la estancia.
• Se coloca la coma en el producto, apartando tantas cifras decimales como las
que reúnan entre todos los factores.
• Coste de 100 fotocopias → 0,025 · 100 = 2,50 €
En la web
a) 17,28 – 12,54 – 4,665
• Se multiplican como si fueran enteros.
• Coste de 10 fotocopias → 0,04 · 10 = 0,40 €
Practica multiplicando números decimales.
Si una hora de aparcamiento cuesta 2,50 €, ¿cuánto pagaremos por una
estancia de tres horas y cuarto (3,25 h)?
Para multiplicar números decimales:
Teniendo en cuenta los precios que anuncia el cartel de la izquierda, calculamos:
d) Desplazar la coma un lugar hacia la izquierda
equivale a multiplicar por diez.
b) 17,28 – (12,54 – 4,665)
10. De un listón de 2 m de longitud se corta un trozo de
0,97 m. ¿Cuánto mide el retal que queda?
d) 12,4 – (18,365 + 7,62)
5. Copia en tu cuaderno y coloca la coma decimal que
falta en cada producto:
a) 2,7 · 1,5 → 405
b) 3,8 · 12 → 456
c) 0,3 · 0,02 → 0006
d) 11,7 · 0,45 → 5265
11. En la carrera de 200 metros lisos, Jon Dalton ha
invertido veintidós segundos y tres décimas, y Bobi García, veintitrés segundos y catorce centésimas.
¿Cuánto tiempo le ha sacado Jon a Bobi?
12. En la ferretería se vende el cable blanco a 0,80 € el
6. Multiplica.
a) 3,26 · 100
b) 35,29 · 10
c) 4,7 · 1 000
d) 9,48 · 1 000
e) –6,24 · 100
f ) 0,475 · (–10)
metro, y el negro, más grueso, a 2,25 € el metro.
¿Cuánto pagaremos por 3,5 m del blanco y 2,25 m
del negro ?
92
Sugerencias
• Se repasan aquí los algoritmos de la suma, de la resta y de la multiplicación de números decimales. Puesto que se trata de procedimientos ya
superados por los estudiantes, podemos profundizar en su justificación,
en la comprobación de las propiedades de estas operaciones y en las
relaciones entre ambas, todo ello siguiendo las mismas pautas que en
los números naturales.
• Los estudiantes practicarán también la resolución de expresiones con
paréntesis y operaciones combinadas, aplicando todo lo aprendido con
números enteros.
• Además, se sugiere trabajar el desarrollo del cálculo mental con números decimales:
– Sumas y restas de cantidades de una y de dos cifras decimales.
– Cálculo con cantidades de dinero (añadir, cambiar, quitar, devolver…).
93
des hacia el aprendizaje cooperativo, se sugiere la siguiente metodología:
• Los estudiantes se distribuyen en parejas o en tríos.
• Resuelven una serie de expresiones individualmente, y después contrastan las soluciones y los procesos.
• Si hay discrepancias, deben descubrir los errores. Si no saben resolver
las dudas o no se ponen de acuerdo, actuará el docente.
Soluciones de “Piensa y practica”
1 a)
1,2b)
0,7c)
3 d)
1,8e)
5 f )
1,75
2 a) – 0,25
b) – 0,3
3 a)6,25 - 7 - 7,75
c) – 0,75
d) 0,05
b)8,05 - 7,9 - 7,75
e) – 0,4
f ) 0,71
c) 1,98 - 2,1 - 2,22
– Construcción de series ascendentes y descendentes.
4 a)
0,075b)
9,405c)
–13,585
– Productos por la unidad seguida de ceros.
5 a)4,05
– Productos por 0,5 (la mitad) y por 1,5 (el triple del anterior, de la mitad).
– Productos por 0,25 (la cuarta parte) y por 0,75.
– Productos por 0,1.
b)45,6
6 a) 326
d) 9 480
7 a)52
Refuerzo y Ampliación
Recomendamos, del cuaderno n.º 3 de EJERCICIOS DE MATEMÁTICAS:
Refuerzo: Ejercicios 1, 2 y 4 de la pág. 4. Ejercicios 1, 2 y 3 de la pág. 5.
Ampliación: Ejercicios 3 y 5 de la pág. 4. Ejercicios 1 a 7 de la pág. 10.
d) 4,44
c) 0,006
d)5,265
b) 352,9
c) 4 700
e) – 624
f ) – 4,75
b)15,08
c) 286
e) 10,881
f ) 0,4112
8 a)7,7
b)3,34
c) 0,8
d)– 0,6
9 a)Falso b)Verdadero
c) Verdadero
d)Falso
10 El retal que queda mide 1,03 m.
Aprendizaje cooperativo
Para esta página, y para todas las destinadas a reforzar la destreza operativa, si el profesor o profesora considera oportuno orientar estas activida-
11 Jon le ha sacado a Bobi 84 centésimas.
12 Pagaremos 7,86 euros.
83
3
División de números decimales
División con números decimales en el divisor
Hasta ahora no hemos abordado divisiones con cifras decimales en el divisor.
Para resolverlas, nos apoyaremos en una propiedad que ya conoces y que ahora
conviene recordar.
Ahora vas a profundizar en lo que sabes sobre la división de números decimales.
Empezaremos con las divisiones de divisor entero.
■ UNA PROPIEDAD IMPORTANTE DE LA DIVISIÓN
Divisor entero. Aproximación del cociente
Ejercicios resueltos
1. Queremos repartir un bidón
de 15 litros de aceite en cuatro garrafas iguales. ¿Cuántos litros pondremos en cada
garrafa?
Compara los ejemplos siguientes:
Vamos a repasar la forma de obtener las cifras decimales del cociente hasta conseguir la aproximación deseada.
15
3
4
3
1 5, 0
3 0
2
4
3,7
Ejemplos
• Si envasamos 15 kilos de ciruelas en 3 cajas, ponemos 5
kilos en cada caja.
15 3
0 5
→ El cociente entero deja un resto de 3 unidades.
Transformamos las tres unidades del resto en 30 décimas
→ y las dividimos entre 4. Por eso ponemos la coma en el
cociente. Sobran 2 décimas.
2. Doña Emilia compra un
queso de un kilo y setecientos
veinticinco gramos, para repartirlo con sus dos hermanas. ¿Qué cantidad de queso
apartará para cada una?
1, 725
3
0
→ 1, 725
2
3
0,5
→ 1, 725
22
15
0
Propiedad de la división: Al multiplicar el dividendo y el divisor por el
mismo número, el cociente no varía.
■ PROCEDIMIENTO PARA ELIMINAR LAS CIFRAS DECIMALES DEL DIVISOR
Cuando el divisor es un número decimal, utilizamos la propiedad anterior
para cambiar la división por otra con el mismo resultado y el divisor entero.
3
0,575
Ejemplo
El camarero llena una jarra con 0,6 litros de leche y en cada café pone, por término
medio, 0,04 litros. ¿Cuántos cafés podrá atender con el contenido de la jarra?
0,6 0,04 ⎯→ Multiplicamos el dividendo y el divisor por 100. Según la propiedad anterior, el cociente no varía.
Solución: Cada hermana se llevará 0,575 kg de queso (575 gramos).
Para obtener el cociente decimal:
· 100
• Al bajar la cifra de las décimas del dividendo, se pone la coma decimal en el
cociente y se continúa la división.
En la web
Practica dividiendo números decimales.
· 100
60
20
0
• Si no hay suficientes cifras decimales en el dividendo, se añaden los ceros
necesarios para lograr la aproximación deseada.
4
15
⎯→ El divisor es ahora un número entero. Ya podemos
hacer la división.
Solución: Podrá poner 60 : 4 = 15 tazas de café.
Cuando hay decimales en el divisor:
Dividir por 10, 100, 1000, …
• Se multiplican el dividendo y el divisor por la unidad seguida de tantos
ceros como cifras decimales haya en el divisor.
Recuerda que para dividir un número por 10, por 100, por 1 000, …, solo hay
que mover la coma hacia la izquierda uno, dos, tres, … lugares.
• Así, la división se transforma en otra de divisor entero. El cociente no varía.
Ejemplos
Ejercicio resuelto
Teniendo en cuenta el peso del paquete de 500 folios, calculamos:
Obtener el cociente de las siguientes divisiones:
• Peso de 100 folios → 2 331 : 5 = 466,2 gramos
• Peso de 10 folios → 466,2 : 10 = 46,62 gramos
· 10
21 : 16,8
168
210
0420
1,25
0840
000
• Peso de 1 folio → 466,2 : 100 = 4,662 gramos
2 331 gramos
• Si envasamos 150 kilos de ciruelas en 30 cajas, ponemos 5 kilos
en cada caja.
150 30
00 5
Observa que al multiplicar por 10 el número de kilos (dividendo) y el número
de cajas (divisor), el resultado no varía.
1 5, 0 4
Continuamos la división transformando las 2 décimas en
3 0 3,75 →
20 centésimas.
20
Solución: Pondremos 3,75 litros en cada garrafa.
0
Para dividir un número decimal por la unidad seguida de ceros, se desplaza
la coma hacia la izquierda tantos lugares como ceros acompañan a la unidad
· 10
· 10 000
0,3 : 0,0025
3000
50
00
· 10 000
25
120
94
Sugerencias
95
– Dividir entre 0,25 es lo mismo que multiplicar por 4.
Para ello, se pueden proponer tandas de ejercicios destinadas a resaltar
los objetivos perseguidos (por ejemplo: 4,7 · 10; 4,7 : 0,1).
• Constatadas en la práctica diaria las dificultades que tienen muchos estudiantes en la división con números decimales, hacemos aquí una revisión detenida de este proceso con una exhaustiva colección de actividades que servirán para completar lagunas y, en cualquier caso, para
afianzar la mecanización de los algoritmos y la aplicación de la operación en la resolución de problemas.
Recomendamos, del cuaderno n.º 3 de EJERCICIOS DE MATEMÁTICAS:
• Comenzamos repasando la división con divisor entero y la aproximación
del cociente al orden de unidades deseado.
Refuerzo: Ejercicios 1 y 2 de la pág. 6. Ejercicios 3 y 4 de la pág. 7. Ejercicios
6, 7 y 8 de la pág. 8.
• En la aproximación decimal del cociente de enteros, razonaremos la colocación de la coma del modo siguiente: las unidades de resto se “cambian a décimas” y se sigue dividiendo. Por tanto, en el cociente se obtendrán décimas. Etcétera.
• A continuación se recuerda la división por la unidad seguida de ceros.
• Antes de abordar las divisiones con decimales en el divisor, revisaremos
una propiedad imprescindible para justificar los procedimientos que se
verán a continuación: si se multiplican el dividendo y el divisor por el
mismo número, el cociente no varía. Con esta propiedad, que nos permite eliminar las cifras decimales del divisor, y los algoritmos ya conocidos, podremos resolver todos los casos de división de decimales.
• Durante la aplicación de la propiedad anterior, conviene hacer la siguiente reflexión: el cociente no varía, pero ¿qué ocurre con el resto? La
resolución de este tipo de cuestiones supone una profundización en la
estructura de la división y en las relaciones entre sus términos.
• Revisaremos también la división por la unidad seguida de ceros, en contraste con la multiplicación estudiada en el epígrafe anterior.
• Por último, dentro del ámbito del cálculo mental, se sugiere trabajar relaciones como:
– Dividir entre 0,1 es lo mismo que multiplicar por 10.
– Dividir entre 0,5 es lo mismo que multiplicar por 2.
84
5
UNIDAD
Refuerzo y Ampliación
Ampliación: Ejercicio 5 de la pág. 7. Ejercicios 9 a 12 de la pág. 9.
ANOTACIONES
4
Piensa y practica
1. Divide mentalmente.
a) 1 : 2
d) 1 : 4
g) 1,2 : 2
j) 0,6 : 3
9. Calcula.
b) 5 : 2
e) 2 : 4
h) 1,2 : 3
k) 0,8 : 4
c) 7 : 2
f) 5 : 4
i) 1,2 : 4
l) 0,9 : 9
b) 53 : 4
e) 6,2 : 5
h) 9 : 7
k) 14,3 : 9
4. Divide.
c) 2 : 1 000
f ) 2,8 : 1 000
i) 0,3 : 1 000
El concepto de raíz cuadrada, que ya conoces, se aplica de la misma forma a los
números decimales.
a = b ↔ b2 = a
= 8,4
b) 2,84 ·
· 1,6 = 1,44
d)
= 4,26
· 2,08 = 2,075
2 8 2 2 = 4 < 7, 5
7, 5 = *
3 8 3 2 = 9 > 7, 5
analiza el ejemplo y calcula.
•
155
0,19
c) 30 : 8
f ) 5 : 234
El cálculo de las aproximaciones por tanteo es lento y molesto, por lo que se suele
recurrir a la calculadora.
c) 0,8 : 1,25
f ) 3,654 : 6,3
7, 5 → 7 . 5 $ → {“…|«°\‘“|}
12. Tres botes de refresco hacen un litro. Expresa en li-
Normalmente, no es necesario tomar todas las cifras decimales que ofrece la máquina, por lo que se redondea a un determinado orden de unidades.
13. Una empresa de mantenimiento de carreteras se
2, 7 8 Redondeo a las décimas.
7, 5 = *
2, 74 8 Redondeo a las centésimas.
tros la capacidad de un bote.
compromete a señalizar 15 kilómetros de una nueva autopista en ocho días. ¿Cuántos kilómetros debe
señalizar por término medio cada día?
Cálculo con lápiz y papel
Recuerda el algoritmo que aprendiste en la unidad 2 para el cálculo de la raíz
cuadrada de números naturales.
Con los números decimales actuarás de la misma forma, teniendo en cuenta que
las cifras se separan de dos en dos, a la derecha y a la izquierda de la coma.
Ejemplo
b) 0,5 : 4
e) 0,08 : 2
en kilos el peso de un yogur.
c) 0,3 : 9
f ) 0,02 : 5
15. ¿Cuántas filas de cajas de 0,2 m × 0,2 m × 0,2 m se
pueden apilar en un contenedor de 1,85 m de altura? ¿Qué hueco quedaría entre la última caja y el
techo del contenedor?
7. Copia en tu cuaderno y completa.
a) 8 : 0,9 = … : 9
c) 2 : 1,37 = … : 137
√ 7 , 50 2
–4
3
14. Un paquete con seis yogures pesa 0,678 kg. Expresa
6. Calcula con tres cifras decimales, si las hay.
a) 0,9 : 5
d) 1,2 : 7
b) 15 : 0,35 = … : 35
d) 7 : 0,009 = … : 9
8. Suprime las comas multiplicando dividendo y divisor
por la unidad seguida de ceros y después calcula con
dos cifras decimales, si las hay.
a) 32 : 0,8
b) 6 : 0,7
c) 1,82 : 0,7
d) 18 : 0,24
e) 0,72 : 0,06
f ) 1,52 : 0,24
g) 7 : 0,05
h) 0,2 : 0,025
i) 11,1 : 0,444
7, 5 = 2, 7…
La raíz cuadrada en la calculadora
→ 5,0 9 → 5,00 9
5 0,5
50 0,55
5
b) 3 : 5
e) 6 : 11
2, 7 8 2, 7 2 = 7, 29 < 7, 5
7, 5 = *
2, 8 8 2, 8 2 = 7, 84 > 7, 5
7, 5 = 2, …
· 100
0,3 : 1,55 ⇒ 30 : 155 ⇒ 30,00
14 50
· 100
0 55
a) 0,4 : 0,84
b) 0,7 : 1,4
d) 2 : 5,4
e) 3,2 : 8,36
5. Observa el ejemplo y calcula el cociente con dos cifras
a) 1 : 4
d) 2 : 9
0, 81 = 0,9 ↔ (0,9)2 = 0,81
Sin embargo, la mayoría de los números no tienen raíz exacta, en cuyo caso trabajamos con aproximaciones.
11. Observa que el dividendo es menor que el divisor,
redondeo
• 86 : 7 = 12,28... ⎯⎯⎯⎯→ 12,3
a) 10 : 3
b) 16 : 9
c) 25 : 7
d) 9,2 : 8
e) 15,9 : 12
f ) 45,52 : 17
decimales.
• 5:9 → 5 9
0
f ) 2,5 : 0,004
c)
c) 35 : 8
f ) 12,5 : 4
i) 169 : 11
l ) 96,7 : 22
b) 8 : 100
e) 5,7 : 100
h) 57,25 : 100
c) 4 : 1,26
e) 1,60 : 0,12
a) 15 ·
3. Calcula y aproxima a las décimas, como en el ejemplo.
a) 5 : 10
d) 3,6 : 10
g) 2,54 : 10
b) 12 : 0,05
d) 0,7 : 0,25
Raíz cuadrada y números decimales
10. Copia en tu cuaderno, calcula y completa.
2. Calcula con dos cifras decimales, si las hay.
a) 28 : 5
d) 7,5 : 3
g) 47 : 3
j) 7,7 : 6
a) 5 : 0,7
5
UNIDAD
16. Los melones se venden a 1,25 €/kg. ¿Cuánto pesa
√ 7 , 50 2,7
–4
47 · 7 = 329
3 50
–3 29
21
√ 7 , 50
–4
3 50
–3 29
21
–16
4
00
2,73
47 · 7 = 329
543 · 3 = 1 629
00
29
71
El proceso puede continuar, añadiendo parejas de ceros en el radicando, hasta
lograr la aproximación deseada.
un melón que cuesta 4,40 €?
17. Para preparar una dosis de cierta vacuna, se nece-
sitan 0,25 mililitros (0,00025 litros) de principio
activo. ¿Cuántas dosis se obtendrán de un litro de
principio activo?
18. Hemos pagado 16,20 € por una pescadilla de
1,32 kilos. ¿A cómo se vende el kilo de pescadilla?
Piensa y practica
1. Calcula mentalmente.
2. Aproxima a las décimas y a las centésimas.
a) 0, 01
b) 0, 09
c) 0, 25
a) 58
b) 7, 2
c) 0, 5
d) 0, 64
e) 0, 0001
f ) 0, 0049
d) 14
e) 8, 5
f ) 0, 03
96
97
Soluciones de “Piensa y practica”
17 4 000 dosis
1 a)
0,5b)
2,5c)
3,5d)
0,25
e)
0,5f )
1,25
18 12,27 €/kg
g)
0,6h)
0,4i )
0,3j )
0,2k)
0,2l )
0,1
2 a)5,6
b)13,25
c) 4,37
d)2,5
e)1,24
f ) 3,12
h) 1,28
i ) 15,36
j ) 1,28
k) 1,58
l ) 4,39
Sugerencias
3 a)3,333… ≈ 3,3
b)1,77… ≈ 1,8
c) 3,571… ≈ 3,6
• El alumnado ya conoce el concepto de raíz cuadrada entera. Ahora se
retoma dicho concepto y se aproxima el valor de una raíz hasta el orden
de unidades deseado.
d)1,15 ≈ 1,2
e)1,325 ≈ 1,3
f ) 2,677… ≈ 2,7
• Para el cálculo de raíces, se ofrecen tres vías:
g) 15,66
4 a)0,5
f ) 0,0028
b)0,08
c) 0,002
d)0,36
g) 0,254
h) 0,5725
i ) 0,0003
e)0,057
5 a)
0,25b)
0,6 c)
3,75d)
0,22e)
0,54f )
0,02
6 a)
0,18 b)
0,125c)
0,033d)
0,171e)
0,04 f )
0,004
7 a)80 : 9
b)1 500 : 35
8 a)320 : 8 = 40
c) 200 : 137
d)7 000 : 9
b)60 : 7 = 8,57
c) 18,2 : 7 = 2,6
d)1 800 : 24 = 75
e)72 : 6 = 12
f ) 152 : 24 = 6,33
g)700 : 5 = 140
h)200 : 25 = 8
i ) 11 100 : 444 = 25
c) 3,17
e)13,33
9 a)7,14
10 a)0,56
11 a)0,47
12 0,33 litros
b)240
b)1,5
b)0,5
d)2,8
c) 0,9
c) 0,64
d)0,37
131,875 km
f ) 625
d)0,9975…
e)0,38
16 3,52 kilos
– la calculadora. Al ofrecer demasiadas cifras decimales, exige aproximar a un determinado orden de unidades. Es práctico, pero conviene
no descuidar el aprendizaje de su correcta utilización.
– el algoritmo. Es menos enriquecedor en cuanto a la construcción de
conceptos, a la vez que más lento y laborioso.
Refuerzo y Ampliación
Recomendamos, del cuaderno n.º 3 de EJERCICIOS DE MATEMÁTICAS:
Refuerzo: Ejercicios 1, 2, 3 y 4 de la pág. 11. Ejercicio 1 de la pág. 12.
Ampliación: Ejercicios 2 y 3 de la pág. 13.
f ) 0,58
140,113 kilos
15 Se pueden apilar 9 filas de cajas. Quedan 0,05 m entre la última caja y
el techo del contenedor.
– el tanteo. Sirve para fijar el concepto. Es enriquecedor desde el punto
de vista del aprendizaje matemático. Se aconseja solamente para números pequeños y con aproximaciones hasta, a lo sumo, las centésimas.
Soluciones de “Piensa y practica”
1 a)0,1
b) 0,3
c) 0,5 d)0,8
e)0,01
2 a)7,6; 7,62
b)2,7; 2,68
c) 0,7; 0,71
d)3,7; 3,74
e)2,9; 2,92
f ) 0,2; 0,17
f ) 0,07
85
9 Hay infinitas posibilidades. Por ejemplo:
1
a)
0,52b)
1,15c)
0,247UNIDAD 5
Ejercicios y problemas
Los números
naturales
Intercala un número decimal entre:
El sistema de numeración
decimal
1.
a) 0,5 y 0,6
d) 6,16 y 6,17
Escribe cómo se leen.
a) 13,4
c) 0,24 y 0,25
f ) 3,2 y 3,01
tramos iguales?
Escribe con cifras.
11.
b) Tres centésimas.
c) Dos unidades y cincuenta y tres milésimas.
0,7
e) Ciento ochenta millonésimas.
Babilonios
2000 a.C.
Aproximar 3,70965 a las…
b) Media décima.
Mayas
0,8
Ejercicio resuelto
12.
Escribe con cifras.
c) Media centésima.
2000 a.C.
3
Escribe los números que dividen el intervalo
0,7-0,8 en cinco partes iguales.
d) Doscientas trece cienmilésimas.
a) Media unidad.
2-3 en cuatro
2
a) Ocho unidades y seis décimas.
3.
b) 1,1 y 1,2
e) 1 y 1,1
b) 0,23
c) 0,145
Todas
las civilizaciones
han tenido un sistema de numeración. Estos han
10.
¿Qué
números
dividen
el intervalo
pasado
de unos pueblos
a otros y han evolucionado
a lo
largo del
tiempo.
e) 0,0006
f ) 0,000148
d) 0,0017
2.
A
9.
→ 4
Unidades
Egipcios
Centésimas → 3,71
d) Un cuarto de unidad.
Romanos
3500 a.C.
Décimas → 3,7
Milésimas → 3,710
100 a.C.
4.
Expresa en décimas.
a) 6 decenas.
b) 27 unidades.
c) 200 centésimas.
d) 800 milésimas.
5.
Copia y completa en tu cuaderno.
a) 8 u = 80 d = … c = … m
b) … u = … d = 30 c = … m
¿Verdadero o falso?
a) Media centésima equivale a 5 décimas.
b) 25 centésimas hacen la cuarta parte de una décima.
c) La cuarta parte de una diezmilésima
equivale a 25
Árabes
700 d.C.
millonésimas.
quedeusamos
Ordena
menor a mayor en cada caso:
!
1,390
1, 39
1,399
1,41
a) 1,4
b) – 0,6
8.
0,9
– 0,8
2,07
–1,03
B
6
M
R
C
6,5
N
2,3
5,28
S
O
5,29
Aproxima a las milésimas.
!
a) 0,62359
b) 1, 7
Chinos
3500 a.C.
c) 0,0999
D
L
E
P 2,4
U
T
Sumas y restas
15.
Calcula mentalmente.
a) ¿Cuánto le falta a 4,7 para valer 5?
b) ¿Cuánto le falta a 1,95 para valer 2?
c) ¿Cuánto le falta a 7,999 para llegar a 8?
Hindúes
500 a.C.
Realiza estas operaciones:
a) 13,04 + 6,528
b) 2,75 + 6,028 + 0,157
c) 4,32 + 0,185 – 1,03
d) 6 – 2,48 – 1,263
17.
Calcula y completa en tu cuaderno.
a) 2,7 + … = 5,2
b) … + 3,08 = 4
sistemas
de –
numeración
c) 1,25
… = 0,4 sirven para
d) …escribir
– 2,015números
= 3,52
os
y, así, recordarlos y transmitirlos. Pero deben servir, también, para
con ellos.
Piensa en siguientes:
el sistema romano (que
18.operar
Opera
las expresiones
ya conoces) y en cómo se las apañarían para efectuar sumas.
a) 5 – (0,8 + 0,6)
Por ejemplo, MCCCXLVI + DCCCXXXIV. ¿Complicado? Pues
Q
b) 2,7que
– (1,6
– 0,85)
imagina lo difícil
tendría
que ser multiplicar.
Asocia un número a cada letra:
A
14.
16.
Orden. Representación.
Redondeo
Sistema decimal
7.
Aproxima, en cada caso, a las unidades, a las décimas y a las centésimas:
a) 2,499
b) 1,992
c) 0,999
Operaciones
c) … u = … d = … c = 1 700 m
6.
13.
c) (3,21 + 2,4) – (2,8 – 1,75)
d) (5,2 – 3,17) – (0,48 + 0,6)
V
1 a)Trece unidades y cuatro décimas.
b)Veintitrés centésimas.
c) Ciento cuarenta y cinco milésimas.
d)Diecisiete diezmilésimas.
e)Seis diezmilésimas.
f ) Ciento cuarenta y ocho millonésimas.
b)0,03
c) 2,053
b)0,05
d)0,00213
c) 0,005
e)0,000180
d)0,25
4 a)6 decenas = 600 décimas
b)27 unidades = 270 décimas
c) 200 centésimas = 20 décimas
d)800 milésimas = 8 décimas
5 a)8 u = 80 d = 800 c = 8 000 m
b)0,3 u = 3 d = 30 c = 300 m
c) 1,7 u = 17 d = 170 c = 1 700 m
6 a)
Falsob)
Falsoc)
Verdadero
!
7 a)1,390 < 1,399 < 1, 39 < 1,4 < 1,41
b)–1,03 < – 0,8 < – 0,6 < 0,9 < 2,07
8 A = 5,9
86
11
13
14
15
16 a)19,568
b)8,935
17
a)2,5
d) 0,8 · 0,5
b)0,92
f ) 4,2 · 0,5
23.
B = 6,3
C = 6,8
D = 7
E = 7,1
M = 2,28
N = 2,34
O = 2,37
P = 2,39
Q = 2,43
R = 5,277
S = 5,285
T = 5,293
U = 5,296
V = 5,3
c) 3,475
d)2,257
c) 0,85
d)5,535
Ejercicio
c) 4,56resuelto
d)0,95
b) 0,62 : 0,1 – 4,3 – 12 · 0,1
Multiplica. ¿Qué
observas?
las multiplcaciones siguientes al estilo egipcio:
1 Efectua
c) 15 · 0,5 + 0,5 : 0,2 – 9,8
a) 6 · 0,5
b) 10
· 0,5
c) 22 · b)
0,541 × 17
a) 17
× 41
e) 1,4 · 0,5
24.
Divide. ¿Qué observas?
18
a)3,6 b) 5 : 0,5
a) 3 : 0,5
b)1,95
c) 11 : 0,5
d) 5,5 · 0,2 + 1,1 + 6,6 : 0,3
31.
3,25 · 2,4 – 1,5 · (2,1 – 3,9) = 7,8 – 1,5 · (–1,8) =
d) 0,4 : 0,5
e) 0,7 : 0,5
f ) 2,1 : 0,5
= 7,8 + 2,7 = 10,5
6
5
multiplicaban
los antiguos hindúes 3,25
3,9
1,5
7,8
25.
Calcula,
observa los sí
resultados
y responde.
3
0
4
7
– 2,1
× 1,8
+ 2,7
En cada
a) 200 · 0,1
30 · –0,1
8 ·casilla
0,1 se pone el resultado de multiplicar ×los2,4
3 2 0 4 2
dos
dígitos
que
la
determinan.
Por
ejemplo,
en
la
ca1300
1,8
120
10,5
ANOTACIONES
1 ¿Qué
5 2le ocurre
8
a un número al multiplicarlo por 0,1?
2
silla sombreada, 4 × 7 = 28.
650
15
1
b)1 7 2: 0,1
0,5 : 0,1
12 35 : –0,1
7,800
2,70
Se suman los resultados en vertical. En cada columna
9 6le ocurre a unsolo
¿Qué
número
cabe al
undividirlo
dígito. por 0,1?
1 2
32.
Calcula.
26. 1 9 7 2Pon
2 ejemplos, investiga, y después completa en tu cuaderno.
a) 1,9 + 2 · (1,3 – 2,2)
a) Multiplicar por 0,2 es igual que dividir entre …
b) 0,36 – 1,3 · (0,18 + 0,02)
Efectúa,
siguiendo
este método,
b) Dividir entre2 0,2
es igual
que multiplicar
por las
… siguientes multiplicaciones:
c) 2,5 – 1,25 · (2,57 – 0,97)
a) 208 × 34
b) 453 × 26
d) 6,5 · 0,2 – 0,4 : (2,705 – 3,105)
27.
Multiplica mentalmente.
3 Comparando estas formas de multiplicar con la nuestra, ¿cuál
e) 12 : 6,4 – 2 · (1 : 8)
a) 18 · 0,1
b) 15 · 0,01
c) 400 · 0,001
te parece más cómoda y efectiva? Justifica tu respuesta.
f ) – (3,5 · 1,2) : 2,1 + (0,865 – 3)
d) 5 · 0,2
e) 200 · 0,02
f ) 3 000 · 0,002
A
g) 20 · 0,5
Soluciones de “Ejercicios y problemas”
3 a)0,5
10
En la web
98
2 a)8,6
multiplicaban los antiguos egipcios
d) sí6,1604
e) 1,06
f ) 3,1
Los egipcios
multiplicaban por duplicaciones sucesivas. 28.
Observa,Divide
por ejemplo,
cómo
mentalmente.
Multiplicación
y división
hacían 23 × 18.
a) 7 : 0,1
b) 9 : 0,01
c) 8 : 0,001
19.
Multiplica.
siguiendo las si2,25;
2,50 y 2,75 Escribían dos columnas de números
d) 2 : 0,2
e) 6 : 0,02
f ) 10 : 0,002
guientes
reglas:
a) 0,6 · 0,4
b) 0,03
· 0,005
←• 1 ⎯→ 18 →
g) 1 : 0,5 1 sin sobrepah) 1 : 0,05
i) 1 : 0,005
la primera, duplicaban sucesivamente
c) 1,3 ·←•
0,082 ⎯→ 36 → d) 15– ·En
0,007
0,72;
0,74; 0,76 y 0,78
sar el primer factor; en nuestro caso, sin pasarse de 23.
e) 2,65←•
· 1,24
· 0,16
4 ⎯→ 72 → f ) 0,25
– La segunda, duplicaban sucesivamente
el segundo
facOperaciones
combinadas
144 decimales,
tor,sienlasnuestro
20.
Calcula 8con dos cifras
hay. ejemplo, 18, tantas veces como habían
a)Unidades
→
2;
Décimas
→
2,5;
Centésimas
→ 2,50
duplicado
1 en la primera
columna.
29.
Ejercicio
resuelto
16
288
←•
⎯→
→
a) 0,8 : 0,3
b) 1,9 : 0,04
– Después, en la primera columna tomaban los
23
414 ← d) 0,024
4,8números
+ 2,6 · 0,5 – 18 · 0,1
c) 5,27→
: 3,2
: 0,015
para que
se obtuviera el primer→ 1,99
b)Unidades → 2; necesarios
Décimas
→al sumarlos
2,0; Centésimas
e) 2,385 : 6,9
f ) 4,6 factor;
: 0,123en nuesro caso, para quer sumaran 23: 4,8 + 1,3 – 1,8
1
+
2
+
4
+
16
=
23
c)Unidades
→ 1; Décimas → 1,0; Centésimas
21.
Multiplica y divide mentalmente.
3→
+ 1,31,00
– Para concluir, cogían, en la segunda columna, los núa) 0,12 · 10
b) 0,12 : 10
meros correspondientes a los sumandos de la primera 4,3
c) 0,002
· 100
d) 0,002
: 100 y los sumaban.
columna
En nuestro caso:
a)
0,624b)
1,778c)
0,100
4,80 + 2,6 · 0,5 – 18 · 0,1 = 4,8 + 1,3 – 1,8 =
e) 0,125 · 1 000
f ) 0,125 : 1 000 18 + 36 + 72 + 288 = 414
= 3 + 1,3 = 4,3
El resultado
de la suma obtenida en la columna de la derecha era el pro22.
Copia y completa
en tu cuaderno.
a)0,3
b)0,05
c) 0,001
ducto buscado. En nuestro ejemplo:
a) 72 : … = 7,2
b) 3,8 : … = 0,038
Opera ayudándote del cálculo mental.
23 × 18 = 41430.
c) … : 1 000 = 0,05
d) … : 100 = 2,3
a) 5,6 – 0,8 : 0,5 + 6,2 · 0,5
h) 20 · 0,05
i) 2 000 · 0,005
Practica las operaciones con decimales.
g) (–5,33 + 1,79) · 3 – (8,75 : 0,5)
99
5
19.
Multiplica.
a) 0,6 · 0,4
c) 1,3 · 0,08
alo
21.
f ) 0,25 · 0,16
24.
25.
a) 0,8 : 0,3
b) 1,9 : 0,04
c) 5,27 : 3,2
d) 0,024 : 0,015
e) 2,385 : 6,9
f ) 4,6 : 0,123
c) 8 : 0,001
b) 0,12 : 10
c) 0,002 · 100
d) 0,002 : 100
f ) 10 : 0,002
i) 1 : 0,005
a) 72 : … = 7,2
b) 3,8 : … = 0,038
c) … : 1 000 = 0,05
d) … : 100 = 2,3
30.
144
→ 23
414 ←
ANOTACIONES
Babilonios
2000 a.C.
b) 0,62 : 0,1 – 4,3 – 12 · 0,1
c) 22 · 0,5
c) 15 · 0,5 + 0,5 : 0,2 – 9,8
d) 0,8 · 0,5
e) 1,4 · 0,5
f ) 4,2 · 0,5
d) 5,5 · 0,2 + 1,1 + 6,6 : 0,3
Divide. ¿Qué observas?
31.
a) 3 : 0,5
b) 5 : 0,5
c) 11 : 0,5
d) 0,4 : 0,5
e) 0,7 : 0,5
f ) 2,1 : 0,5
– La segunda, duplicaban sucesivamente el segundo factor, en nuestro ejemplo, 18, tantas veces como habían
duplicado 1 en la primera columna.
f ) – 4,135
g) –28,12
– Después, en la primera columna tomaban los números
necesarios para que al sumarlos se obtuviera el primer
factor; en nuesro caso, para quer sumaran 23:
1 + 2 + 4 + 16 = 23
– Para concluir, cogían, en la segunda columna, los números correspondientes a los sumandos de la primera
columna y los sumaban. En nuestro caso:
18 + 36 + 72 + 288 = 414
Opera ayudándote del cálculo mental.
b) 10 · 0,5
– En la primera, duplicaban sucesivamente 1 sin sobrepa-
El resultado de la suma obtenida en la columna de la derecha era el producto buscado. En nuestro ejemplo:
23 × 18 = 414
a) 5,6 – 0,8 : 0,5 + 6,2 · 0,5
Multiplica. ¿Qué observas?
1
Chinos
3500 a.C.
Efectua las multiplcaciones siguientes al estilo egipcio:
a) 17 × 41
b) 41 × 17
Ejercicio resuelto
3,25 · 2,4 – 1,5 · (2,1 – 3,9) = 7,8 – 1,5 · (–1,8) =
= 7,8 + 2,7 = 10,5
3,25
× 2,4
1300
650
7,800
Calcula, observa los resultados y responde.
Árabes
8 700
· 0,1
d.C.
¿Qué le
ocurre
a un número al dividirlo por 0,1?
que
usamos
Pon ejemplos, investiga, y después completa en tu cuaderno.
32.
L
3,9
1,5
– 2,1
× 1,8
1,8
120
Hindúes
500 a.C.
15
2,70
6
7,8
+ 2,7
10,5
1
12
9 6
1 2
1 9 7 2 2
Calcula.
a) 1,9 + 2 · (1,3 – 2,2)
os sistemas
de –
numeración
b) 0,36
1,3 · (0,18 sirven
+ 0,02)para escribir números
y, así, recordarlos y transmitirlos. Pero deben servir, tamc) 2,5con
– 1,25
· (2,57
– 0,97)
bién, para operar
ellos.
Piensa
en el sistema romano (que
ya conoces)d)
y 6,5
en cómo
las: apañarían
para efectuar sumas.
· 0,2 –se0,4
(2,705 – 3,105)
Por ejemplo, MCCCXLVI + DCCCXXXIV. ¿Complicado? Pues
e) 12que
: 6,4tendría
– 2 · (1que
: 8)ser multiplicar.
0,001imagina lo difícil
b) Dividir entre 0,2 es igual que multiplicar por …
a) 18 · 0,1
b) 15 · 0,01
d) 5 · 0,2
e) 200 · 0,02
f ) 3 000 · 0,002
f ) – (3,5 · 1,2) : 2,1 + (0,865 – 3)
g) 20 · 0,5
h) 20 · 0,05
i) 2 000 · 0,005
g) (–5,33 + 1,79) · 3 – (8,75 : 0,5)
Practica las operaciones con decimales.
5
3 0 7
3 2 0 4 2
1 5 2 8
2
2 1
4
a) Multiplicar por 0,2 es igual que dividir entre …
En la web
72 →
←• 16 ⎯→ 288 →
= 3 + 1,3 = 4,3
a) 6 · 0,5
guientes reglas:
32 a)
0,1b)
2,3
sar el 0,1c)
primer factor; en nuestro caso, sin0,5d)
pasarse de 23.
4,3
4,80 + 2,6 · 0,5 – 18 · 0,1 = 4,8 + 1,3 – 1,8 =
3500 a.C.
100 a.C.
c) 400 ·
18 →
36 →
Egipcios
Copia y completa en tu cuaderno.
Multiplica mentalmente.
←• 1 ⎯→
←• 2 ⎯→
←• 4 ⎯→
4,8 + 1,3 – 1,8
f ) 0,125 : 1 000
Romanos
i ) 200
Escribían
dos columnas de números siguiendo
las si30 a)
7,1b)
0,7c)
0,2d)
24,2
8
e) 1,625
3 + 1,3
a) 0,12 · 10
30 · 0,1
Los egipcios multiplicaban por duplicaciones sucesivas. Observa, por ejemplo, cómo
hacían 23 × 18.
4,8 + 2,6 · 0,5 – 18 · 0,1
b) 7 : 0,1
: 0,1
0,5 : 0,1
Sistema 35
decimal
27.
f ) 5 000
Ejercicio resuelto
29.
¿Qué le ocurre a un número al multiplicarlo por 0,1?
26.
b) 9 : 0,01
Multiplica y divide mentalmente.
a) 200 · 0,1
57
e) 300
Operaciones combinadas
Calcula con dos cifras decimales, si las hay.
Mayas
23.
d) 10
28.
a) 7 : 0,1
e) 0,125 · 12000
000
a.C.
22.
c) 8 000
Así2multiplicaban los antiguos egipcios
g)
h) 20
d) 2 : 0,2
e) 6 : 0,02
b) 0,03 · 0,005
Todas las civilizaciones han tenido un sistema de numeración. Estos han
g) 1 : 0,5a lo largo del
h) 1tiempo.
: 0,05
pasado de unos
d) 15pueblos
· 0,007 a otros y han evolucionado
e) 2,65 · 1,24
20.
b) 900
Los números naturales
Divide mentalmente.
Multiplicación y división
tro
éci-
1
28 a) 70
5
UNIDAD
2
Así multiplicaban los antiguos hindúes
– En cada casilla se pone el resultado de multiplicar los
dos dígitos que la determinan. Por ejemplo, en la casilla sombreada, 4 × 7 = 28.
– Se suman los resultados en vertical. En cada columna
solo cabe un dígito.
Efectúa, siguiendo este método, las siguientes multiplicaciones:
a) 208 × 34
3
b) 453 × 26
Comparando estas formas de multiplicar con la nuestra, ¿cuál
te parece más cómoda y efectiva? Justifica tu respuesta.
99
Soluciones de “Ejercicios y problemas”
19 a)0,24
b)0,00015
c) 0,104
d)
0,105e)
3,286f )
0,04
20 a)
2,66b)
47,5c)
1,64
d) 1,6
21 a)1,2
d) 0,00002
22 a)10
e) 0,34
f ) 37,39
b)0,012
c) 0,2
e) 125
f ) 0,000125
b)100
c) 50
d)230
23 a)
3b)
5c)
11
d)
0,4e)
0,7f )
2,1
Multiplicar por 0,5 es lo mismo que dividir entre 2.
24 a)6
b)10
c) 22
d)
0,8e)
1,4f )
4,2
Dividir entre 0,5 es lo mismo que multiplicar por 2.
25 a)200 · 0,1 = 20; 30 · 0,1 = 3; 8 · 0,1 = 0,8
Multiplicar un número por 0,1 es lo mismo que dividirlo entre 10.
b)7 : 0,1 = 70; 35 : 0,1 = 350; 0,5 : 0,1 = 5
Dividir un número entre 0,1 es lo mismo que multiplicarlo por 10.
26 a)Multiplicar por 0,2 es igual que dividir entre 5.
b)Dividir entre 0,2 es igual que multiplicar por 5.
27 a)1,8
b)0,15
c) 0,4
d)
1e)
4f )
6
g) 10
h) 1
i ) 10
87
UNIDAD
Ejercicios y problemas
Raíz cuadrada
Utiliza la calculadora
Resuelve problemas
33.
36.
39.
Calcula mentalmente.
a) 0, 04
b) 0, 16
c) 0, 36
d) 0, 0009
e) 0, 0025
f ) 0, 0081
34.
• 1,42 – 2,4 · (2,15 – 1,6) ⇒
⇒ 2,15 - 1,6 = * 2,4 µ 1,42 ≤ Ñ ⇒ {∫∫≠Ÿ‘}
1,42 – 2,4 · (2,15 – 1,6) = 0,1
Copia y completa en tu cuaderno.
√3
–3
0
–
35.
8, 0 0
,
6
12
2
1 2 1
0
·
√5, 7 0
,
–4
4 ·
1
a) 2,75 – 0,5 · (1,69 – 0,38)
b) 2,3 · (6,07 – 1,34) – 0,45
37.
0
b) 32, 8
38.
c) 1425
b) 217
2.°
90,16
3.°
4.°
88,815 87,801
5.°
6.°
86,9
86,15
b) ¿Cuánto ha adelgazado en total?
Con 15 kilos de miel se han llenado 25 frascos.
¿Cuál es el peso de cada frasco, teniendo en cuenta
que el casco y la tapa pesan 0,12 kg?
41.
Un coche avanza 2,68 metros por cada vuelta que
da la rueda. ¿Cuántas vueltas dará en el trayecto de
620 kilómetros entre Madrid y Barcelona? (Aproxima el resultado a las centenas).
c) 2 829
Aprende a resolver problemas
Un bodeguero compra una partida de 30 000 litros de vino por 72 000 € y los envasa
en botellas de 75 centilitros. Las botellas, vacías, le salen a 14 € la centena, y los corchos,
a 10 € el millar. ¿A cómo debe vender la botella para obtener 54 000 € de beneficios?
42.
Cuatro tazas pesan lo mismo que cinco vasos. Si
cada taza pesa 0,115 kg, ¿cuánto pesa cada vaso?
Comprueba que has entendido el enunciado.
43.
Una empresa de productos lácteos vende los yogures a 1,20 € la unidad. De esa cantidad, la tercera parte corresponde al envase; la mitad, a costes de
producción, comercialización y ganancias, y el resto,
al contenido. ¿Cuánto cuesta el contenido?
44.
Raquel ha hecho este trimestre tres exámenes
de matemáticas y ha sacado un 5,5, un 7 y un 2,40.
¿Cuál es su nota media?
45.
El cesto del panadero, vacío, pesa 8,5 kg; y cargado con barras de 250 gramos pesa 18,750 kg. ¿Cuántas barras hay en el cesto?
46.
Se desea cercar la finca que aparece en la figura
con una valla de alambrada que se vende, por rollos
de 5 metros, a 12,99 € el rollo. ¿Cuál será el presupuesto para la alambrada?
¿Qué compra? ¿Qué hace con lo que compra? ¿Qué elementos necesita para llevar
a cabo su propósito y cuánto le cuestan? ¿Qué quiere conseguir?
Piensa en el camino que vas a seguir para resolver el problema. ¿Qué necesitas saber?
¿Por qué no empiezas calculando el número de botellas necesarias para envasar todo el vino?
— Buena idea, así podré calcular luego el coste del vino que va en una botella y
a cuánto ha de ascender la ganancia por botella:
30 000 : 0,75 = 40 000 botellas
¿Puedes ahora calcular el coste
de cada uno de los elementos
que permiten producir una botella?
— Veamos… necesito una botella vacía, un corcho y, por supuesto, el vino:
Botella vacía: 14 : 100 = 0,14 €
Corcho: 10 : 1 000 = 0,01 €
Vino: 72 000 : 40 000 = 1,80 €
Si se quieren ganar 54 000 €
en total, ¿cuánto hay que ganar
con cada botella?
— Esto es fácil. Como son 40 000 botellas…
54 000 : 40 000 = 1,35 € tiene que ganar por botella
Pues si ya tienes los
gastos y la ganancia
por botella…
— Ya está, lo sumo todo y listo:
0,14 + 0,01 + 1,80 + 1,35 = 3,30 €
Solución: El precio de cada botella será de 3,30 €.
100
9,85 m
5,75 m
19,95 m
28,2 m
— Una bolsa de bacalao de 0,92 kg a 13,25 €/kg.
— Un paquete de galletas que cuesta 2,85 €.
— Un cuarto de kilo de jamón a 38,40 €/kg.
¿Cuánto pagan en caja por la compra?
48.
Una merluza de kilo y cuarto ha costado 15,75 €.
¿Cuánto costará otra merluza que pesa 1,4 kilos?
49.
¿Cuántas baldas de 0,8 m de longitud y
0,25 m de anchura puede obtener un carpintero, cortando un tablero de 2,40 m × 1,75 m?
Problemas “+”
50.
Una nave de exposiciones mide 20,25 m de ancho por 35,8 m de largo. Para limpiar el suelo, se
utiliza la máquina fregadora y enceradora capaz de
cubrir una superficie de 1 000 m2 a la hora. ¿Dará
tiempo a limpiar la nave en tres cuartos de hora?
51.
Martina tiene dos teléfonos móviles contratados en dos compañías diferentes, A y B. La compañía telefónica A cobra 30 céntimos por establecimiento de llamada y 20 céntimos al minuto. La compañía B no cobra establecimiento de llamada, pero
cobra 25 céntimos por minuto.
Explica brevemente qué teléfono le conviene usar a
Martina, dependiendo del tiempo previsto para la llamada.
52.
Las tablas siguientes recogen los tiros a canasta
y las canastas conseguidas por dos jugadores en los
cinco últimos partidos.
JUGADOR A
1.°
2.°
3.°
4.°
5.°
TIROS
4
3
4
2
5
CANASTAS
2
3
3
2
4
JUGADOR B
1.°
2.°
3.°
4.°
5.°
TIROS
5
7
3
8
7
CANASTAS
2
5
2
7
5
¿Cuál de los dos jugadores crees que tiene el tiro más
seguro? Justifica tu respuesta.
101
41 231 343,2835… vueltas que, aproximando a las centenas, son 231 300
vueltas.
En este apartado, mediante el seguimiento de un ejemplo, se pretende
ofrecer modelos, estrategias y pautas para resolver problemas.
• Para explotar al máximo los objetivos de este apartado, podemos pedir
a los alumnos y a las alumnas que resuelvan previamente el problema,
buscando cada uno su propio camino. Y después, en gran grupo, contrastar los distintos procesos seguidos, la calidad de cada exposición,
etc. Terminaremos analizando el desarrollo que incluye la página.
33 a)0,2
b)0,4
c) 0,6
34 √ 3 8, 0 0 6 , 1
0 2 0 0
– 1 2 1
0 7 9
d)0,03
e)0,05
f ) 0,09
5, 7 0 2 , 3
√
– 4 4 3 · 3
12 1 · 1
37 a)6,48
38 a)3,60555… → 3,61 b)10,429
b)15,16
c) 37,74
b)14,7309… → 14,73
c)53,1883… → 53,19
39 a)Ha adelgazado más el segundo mes del régimen.
b)En total ha adelgazado 91,38 – 86,15 = 5,23 kilos.
40 El peso de cada frasco es de 0,72 kilos.
44 Nota media: 4,9666… (4,97 si se aproxima a las centésimas; y 5 si se
aproxima a las décimas o a las unidades).
45 En el cesto hay 41 barras.
47 Pagan 29,89 €.
48 Costará 17,64 euros.
49 Puede obtener 21 baldas.
51 Si la llamada dura menos de 6 minutos, le conviene usar la compañía
0 4 1
35 a)
2,4b)
5,7c)
11,7
36 a)2,095
43 El contenido cuesta 0,20 euros.
50 Sí, podrá cumplir el trabajo en tres cuartos de hora.
1 7 0
1 2 9
42 Un vaso pesa 92 g.
46 259,80 euros
Soluciones de “Ejercicios y problemas”
– 3 6 Rosa y Javier compran en el supermercado:
— Cinco litros de leche a 1,05 € el litro.
Resuelve problemas con números decimales.
En la web
Aprende a resolver problemas
88
1.°
91,38
40.
Haz con la calculadora y aproxima a las centésimas.
a) 13
c) 138, 85
b) 230
47.
Tras consultar con su dietista, el señor Horondo se
ha puesto a régimen. En la tabla ha recogido los resultados de la báscula tomados el primer día de cada uno de
los seis últimos meses:
a) ¿En qué mes ha adelgazado más?
Calcula con lápiz y papel, sacando dos cifras decimales, y después comprueba con la calculadora.
a) 42
Calcula con una cifra decimal.
a) 5, 76
Observa el ejemplo y resuelve con la calculadora.
5
B; si la llamada dura 6 minutos le da igual una compañía u otra, y si
dura más de 6 minutos, le conviene usar la A.
52 El jugador A (por cada tiro encesta 0,777… canastas) tiene el tiro un
poco más seguro que el jugador B (por cada tiro encesta 0,7 canastas).
ANOTACIONES
Taller de matemáticas
Entrénate resolviendo problemas
Lee e infórmate
Echa cuentas… y un poco de ingenio
Escritura de los números decimales
• Tengo en el bolsillo 25 monedas. Todas son de 0,50 € o de 0,20 €. En total tengo
Los números decimales se conocen desde la antigüedad, pero la forma en que los escribimos es bastante reciente.
8 €. ¿Cuántas monedas tengo de cada clase?
• Tengo 3,45 € en monedas de 1 €; 0,50 €; 0,20 € y 0,05 €. Hay menos de diez mone-
Los primeros pasos hacia la escritura actual se dieron en Europa con la llegada del sistema
de numeración decimal en la segunda mitad el siglo xvi. Por esa época, aparecen tratados
en los que cada cifra decimal iba acompañada de su órden de unidades. Por ejemplo, para
escribir 12,58 ponían:
das. ¿Cuántas hay de cada tipo? (Encuentra más de una solución).
• Consigue el número 10 multiplicando tres números diferentes.
• Tres amigos motoristas, Roberto Rojo, Bartolomé Blanco y Genaro Gris,
Como ves, (0) indicaba la parte entera; (1), la cifra de las décimas; (2), las centésimas, etc.
se disponen a salir de paseo:
El siguiente paso fue la separación de la parte entera de la parte decimal colocando un circulito encima de la cifra de las unidades:
—¿Os habéis fijado —dice Roberto— que una de nuestras motos es roja,
otra blanca y otra gris, pero en ningún caso el color coincide con el apellido
del dueño?
12(0) 5(1) 8(2) ⎯→ 12̊ 58
A comienzos del siglo xvii, matemáticos italianos y holandeses comenzaron a utilizar un punto o una coma para este propósito. Pero no fue hasta la publicación
de los trabajos del matemático escocés John Napier (1550-1617), quien utilizaba
ambos de forma indistinta, cuando se popularizaron estas formas de escribir los
números decimales. Mientras que en la Europa continental se adoptó la coma
decimal, en las Islas Británicas y en los demás países anglosajones se prefirió el
punto, notación que ha pasado también a las calculadoras y a los ordenadores.
—Pues no me había fijado —dice el de la moto blanca—, pero tienes razón.
¿De qué color es la moto de cada uno?
John Napier
emprender
aprender
Investiga y exprésate
2:9
0,22222…
0,1
0,1
19 : 9
…
d) 2,6 : 100
8. Calcula.
…
— ¿Qué tienen en común estos números?
— ¿Qué tienen en común los cocientes?
c) Haz lo mismo con los números de estas series:
2 - 11 - 20 - 29 - 38 - …
3 - 12 - 21 - 30 - 39 - …
4 - 13 - 22 - 31 - 40 - …
…
¿Qué observas?
d) Continúa haciendo pruebas y anotando ordenadamente los resultados. Después, expresa por escrito tus
conclusiones.
b) 0,1 < … < 0,11
5. Redondea a las décimas y a las centésimas.
!
b) 5,6
a) 2,726
6. ¿Qué número señala cada letra?:
A
B
d) 4,2 – (0,2 · 5 – 0,6)
9. Calcula con dos cifras decimales.
a) 7 : 13
b) 54,5 : 12
c) 8,34 : 15,25
11. Manuel trabaja de forma eventual, en una tienda,
envolviendo paquetes de regalo. Por cada paquete
le dan ochenta céntimos. Ayer hizo 30 paquetes.
¿Cuánto ganó?
12. Para hacer un regalo a Rosa, debemos poner 33 €
2,9
2,8
b) 4,2 – 0,2 · (5 – 0,6)
c) (4,2 – 0,2) · 5 – 0,6
melón de 2,800 kilos?
4. Copia y completa con un número decimal.
a) 4,5 < … < 4,6
a) 4,2 – 0,2 · 5 – 0,6
10. El melón se vende a 1,75 €/kg. ¿Cuánto costará un
2,07 - 0,27 - 2,71 - 2,7 - 2,17
)
1,1111…
b) 2,8 · 3,75
c) 6,8 · 100
b) ¿Cuántas millonésimas hay en una milésima?
1 - 10 - 19 - 28 - 37 - …
10 : 9
a) 2,8 – 3,75 + 1,245
b) Dos unidades y siete centésimas.
3. Ordena de menor a mayor y representa en la recta.
b) Ahora, divide entre 9 varios números de esta serie:
0,1111…
a) Veintiocho milésimas.
a) ¿Cuántas milésimas hacen una décima?
…
Resoluciones de estos ejercicios.
7. Calcula.
2. Piensa y contesta.
3:9
1:9
En la web
1. Escribe con cifras.
d) Nueve millonésimas.
)
0,11111…
Autoevaluación
c) Ciento treinta y dos diezmilésimas.
• a) Completa varias filas de esta tabla usando la calculadora:
1:9
? × ? × ? = 10
(Encuentra más de una solución).
12(0) 5(1) 8(2)
…
5
UNIDAD
C
D
entre 10 amigos. Para hacer un regalo a mi madre,
debemos poner 10 euros entre sus 3 hijos. ¿Cuál de
los dos regalos me sale más caro?
102
Lee e infórmate
103
Entrénate resolviendo problemas
Escritura de los números decimales
Echa cuentas… y un poco de ingenio
El texto incluye algunas anécdotas relativas a la evolución de la notación
decimal. Con ello, los alumnos y alumnas comprobarán que algo que perciben como un recurso acabado, sencillo y natural, es un aprendizaje conseguido tras mucho esfuerzo a lo largo de la historia.
Soluciones
Investiga y exprésate
Se sugiere abordar las actividades en pequeño grupo, poniendo en común las soluciones de cada apartado antes de pasar al siguiente.
La concreción por escrito de los procesos y las soluciones fija los aprendizajes conseguidos y desarrolla procedimientos y capacidades, en el terreno de la expresión y del pensamiento, tan valiosos como las empleadas
en la etapa de investigación.
Soluciones
!
! !
!
!
!
a)Se obtiene 0, 1; 0, 2; 0, 3; 0, 4; 0, 5; 0, 6; …
!
!
!
!
!
!
b)Se obtiene 0, 1; 1, 1; 2, 1; 3, 1; 4, 1; 5, 1; …
– Los números 1 - 10 - 19 - 28… dejan de resto 1 al dividirlos entre 9.
!
– Los cocientes tienen en común la parte decimal: 0,111… = 0, 1 .
! !
!
!
!
c)Primera serie: 0, 2; 1, 2; 2, 2; 3, 2; 4, 2; … Dejan de resto 2 al dividirlos
entre 9.
! ! !
!
!
Segunda serie: 0, 3; 1, 3; 2, 3; 3, 3; 4, 3; … Dejan de resto 3 al dividirlos
entre 9.
! ! ! !
!
Tercera serie: 0, 4; 1, 4; 2, 4; 3, 4; 4, 4; … Dejan de resto 4 al dividirlos
entre 9.
d)La división entera de un número entre 9 deja un resto, r, comprendido
entre 0 y 8, ambos inclusive. La parte decimal del cociente está formada
por la cifra “r” (resto de la división entera), repetida indefinidamente.
• Hay 15 monedas de 0,20 € y 10 monedas de 0,50 €.
• Solución 1 → 2 de 1 € + 2 de 0,50 € + 2 de 0,20 € + 1 de 0,05 €
Solución 2 → 1 de 1 € + 4 de 0,50 € + 2 de 0,20 € + 1 de 0,05 €
• Por ejemplo, 10 = 1,25 · 4 · 2 ; 10 = 0,25 · 20 · 2
• R. Rojo, gris; B. Blanco, roja; G. Gris, blanca.
Soluciones de la autoevaluación
1 a)0,028
b)2,07
2 a) 100
c) 0,0132
d)0,000009
b) 1 000
3 0,27 < 2,07 < 2,17 < 2,7 < 2,71
4 a)4,5 < 4,55 < 4,6
5 A las décimas: a) 2,7; b) 5,7
b)0,1 < 0,105 < 0,11
A las centésimas: a) 2,73; b) 5,67
6 A → 2,78
B → 2,85
C → 2,925
D→3
7 a)0,295
b)10,5
c) 680
d)0,026
8 a)2,6
b)3,32
c) 19,4
d)3,8
9 a)
0,53b)
4,54c)
0,54
10 El melón costará 4,90 €.
11 24 euros.
12 Sale más caro el regalo de la madre (3,33 € cada uno) que el regalo
de Rosa (3,30 € cada uno).
89