Unidad 7 Problema adicional
Anuncio
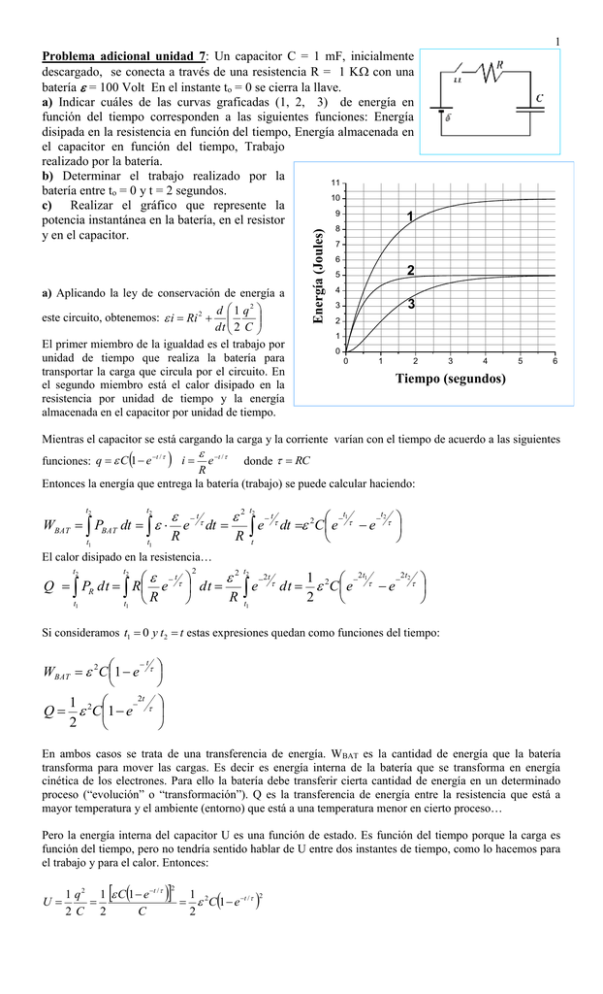
1 a) Aplicando la ley de conservación de energía a d 1 q2 este circuito, obtenemos: i Ri 2 dt 2 C El primer miembro de la igualdad es el trabajo por unidad de tiempo que realiza la batería para transportar la carga que circula por el circuito. En el segundo miembro está el calor disipado en la resistencia por unidad de tiempo y la energía almacenada en el capacitor por unidad de tiempo. Energía (Joules) Problema adicional unidad 7: Un capacitor C = 1 mF, inicialmente descargado, se conecta a través de una resistencia R = 1 K con una batería = 100 Volt En el instante to = 0 se cierra la llave. a) Indicar cuáles de las curvas graficadas (1, 2, 3) de energía en función del tiempo corresponden a las siguientes funciones: Energía disipada en la resistencia en función del tiempo, Energía almacenada en el capacitor en función del tiempo, Trabajo realizado por la batería. b) Determinar el trabajo realizado por la 11 batería entre to = 0 y t = 2 segundos. 10 c) Realizar el gráfico que represente la 9 1 potencia instantánea en la batería, en el resistor 8 y en el capacitor. 7 6 2 5 4 3 3 2 1 0 0 1 2 3 4 5 6 Tiempo (segundos) Mientras el capacitor se está cargando la carga y la corriente varían con el tiempo de acuerdo a las siguientes funciones: q C 1 e t / i e t / donde RC R Entonces la energía que entrega la batería (trabajo) se puede calcular haciendo: t2 t2 WBAT PBAT dt t1 t1 R e t dt 2 R t2 e t t t 2 t1 dt 2C e e El calor disipado en la resistencia… 2t 2 2 t 1 2 2t1 2 t Q PR dt R e dt e dt C e e R R t1 2 t1 t1 t2 2 t2 2 t Si consideramos t1 0 y t2 t estas expresiones quedan como funciones del tiempo: t WBAT 2C 1 e 2t 1 2 Q C1 e 2 En ambos casos se trata de una transferencia de energía. WBAT es la cantidad de energía que la batería transforma para mover las cargas. Es decir es energía interna de la batería que se transforma en energía cinética de los electrones. Para ello la batería debe transferir cierta cantidad de energía en un determinado proceso (“evolución” o “transformación”). Q es la transferencia de energía entre la resistencia que está a mayor temperatura y el ambiente (entorno) que está a una temperatura menor en cierto proceso… Pero la energía interna del capacitor U es una función de estado. Es función del tiempo porque la carga es función del tiempo, pero no tendría sentido hablar de U entre dos instantes de tiempo, como lo hacemos para el trabajo y para el calor. Entonces: 1 q 2 1 C 1 e t / U 2C 2 C 2 1 2C 1 e t / 2 2 La función WBAT tiene un tiempo característico = RC. Es asintótica a C. Su pendiente en el origen es 2C/. Entonces la recta tangente pasa por el punto t = y WBAT =2C. 2 2 La curva 1 es la que tiene estas propiedades. La función Q tiene un tiempo característico /2. Es asintótica a 1/22C. La pendiente en el origen es 2C/. Entonces la recta tangente es la misma que para la función anterior. La curva 2 es la que tiene estas propiedades. La función U es asintótica a 1/22C. La pendiente en el origen es nula como se puede comprobar haciendo la derivada de U con respecto al tiempo y luego hacer t = 0. Haciendo la derivada segunda e igualando a cero se puede comprobar que la curva tiene un punto de inflexión (cambia de concavidad positiva a concavidad negativa) en el valor de tiempo t = ln2 0,69 RC. La curva 3es la que tiene estas propiedades. Utilizando los datos numéricos del problema resulta… RC 1103 1103 F 1 seg t t 2 WBAT 100V 1103 F 1 e 1 s 101 e 1 ( Joules) 2t t 1 2 Q 100V 1103 F 1 e 1 s 51 e 0,5 ( Joules) 2 2 2 t 1 t 2 U 100V 1103 F 1 e 1 s 51 e 1 2 ( Joules) Se puede verificar que WBAT Q U t t t 101 e 1 51 e 0,5 51 e 1 2 2e t 1 1 e 2t 1 1 2e t 1 e 2t 2 1 b) 2 WBAT 101 e 1 8,6466 Joules 2 Q 51 e 0,5 4,9084 Joules 2 2 U 51 e 1 3,7382 ( Joules) c) Esta parte se puede resolver utilizando las expresiones de la carga y de la corriente en función del tiempo para la el régimen transitorio (variable con el tiempo) de carga del capacitor. PBAT i PR R i 2 2 R 2 R dU d 1 q 2 dt dt 2 C e e t 2t 2 t 2t e e R PBAT es el trabajo por unidad de tiempo (instantáneo) que realiza la batería para transportar una cantidad de carga dq El trabajo que realiza la batería es: 3 t2 WBAT PBAT dt t1 PR es la cantidad de calor por unidad de tiempo (instantánea) que se está disipando en la resistencia R al pasar por ella una cantidad de carga dq La cantidad de calor Q que se disipa en la resistencia en un lapso de tiempo es: t2 Q PR dt t1 Como se puede comprobar la energía que se almacena en el capacitor es igual a la diferencia entre el trabajo que realiza la batería y el calor que se disipa en la resistencia (Primer principio de la termodinámica) En el siguiente gráfico se muestran las curvas que corresponden a la potencia instantánea de la batería, el calor por unidad de tiempo disipado en la resistencia y la energía almacenada en el capacitor por unidad de tiempo, todas en función del tiempo. Estas tres curvas son las derivadas de las curvas del gráfico anterior. Potencia instantánea de la batería Calor por unidad de tiempo disipado en R Energía por unidad de tiempo acumulada en C 11 Potencia (Watt = Joule /seg) 10 9 8 7 6 5 4 3 2 1 0 0 1 2 Tiempo (segundos) 3 4 = 1 seg Observaciones: Las curvas 1, 2 y 3 del gráfico propuesto en el enunciado se pueden obtener realizando las integrales entre 0 y un instante t de cada una de las funciones que se obtuvieron en la parte c. En el gráfico de potencias “curva roja + curva violeta = curva negra”. ¿Cuál es el significado físico de esta afirmación? En el gráfico de energías “curva 2 +curva 3 = curva 1”. ¿Por qué? La curva 3 parece tener un punto de inflexión en algún instante comprendido entre 0,5 y 1 segundo. La curva roja tiene un máximo en algún instante comprendido entre 0,5 y 1 segundo.