Problema. Un cazador acostado en el suelo, lanza una flecha con

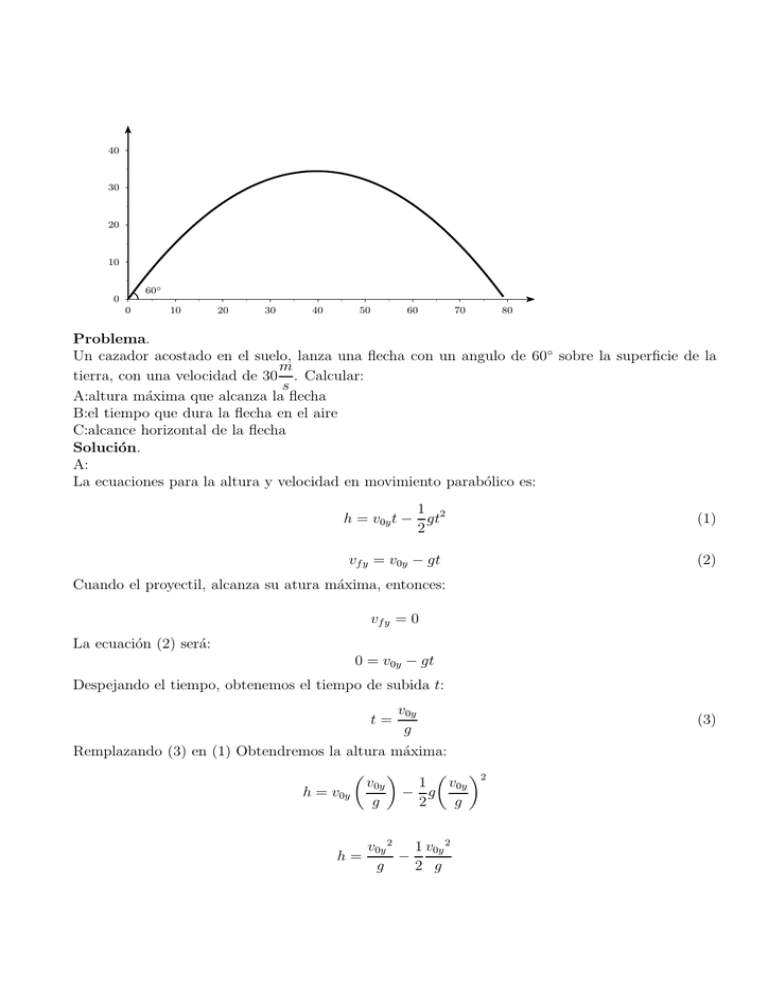
b
b
b
b
b
40
30
20
10
60◦
0
0
10
20
30
40
50
60
70
80
Problema.
Un cazador acostado en el suelo, lanza una flecha con un angulo de 60◦ sobre la superficie de la
m
tierra, con una velocidad de 30 . Calcular:
s
A:altura máxima que alcanza la flecha
B:el tiempo que dura la flecha en el aire
C:alcance horizontal de la flecha
Solución.
A:
La ecuaciones para la altura y velocidad en movimiento parabólico es:
1
h = v0y t − gt2
2
(1)
vf y = v0y − gt
(2)
Cuando el proyectil, alcanza su atura máxima, entonces:
vf y = 0
La ecuación (2) será:
0 = v0y − gt
Despejando el tiempo, obtenemos el tiempo de subida t:
t=
v0y
g
Remplazando (3) en (1) Obtendremos la altura máxima:
2
1 v0y
v0y
− g
h = v0y
g
2
g
h=
v0y 2 1 v0y 2
−
g
2 g
(3)
h=
1 v0y 2
2 g
La componente vertical de la velocidad inicial es:
v0y = v0 sin (60)
Remplazando en la altura máxima:
h=
1 (v0 sin (60))2
2
g
1 (30 sin (60))
h=
2
10 sm2
2 m2
s2
h = 33.75m
B:
El tiempo de vuelo es dos veces el tiempo de subida:
tv = 2t
Remplazando (3):
tv = 2
v0y
g
Remplazando la componente vertical:
v0 sin (60)
g
30 m sin (60)
tv = 2 s m
10 s2
tv = 2
tv = 5.19s
C:
El alcance máximo es:
x = v0x tv
(4)
La componente horizontal de la velocidad inicial es:
v0x = v0 cos (60)
Remplazando el tiempo de vuelo tv , de (4), la componente horizontal de la velocidad inicial, en el
alcance máximo tenemos:
x = v0 cos (60) 2
x=
v0 sin (60)
g
v0 2 2 sin (60) cos (60)
g
v0 2 sin (2 (60))
x=
g
x=
v0 2 sin (120)
g
2
(30)2 sin (120) ms2
x=
10 sm2
x = 77.94m