Resumen de los temas

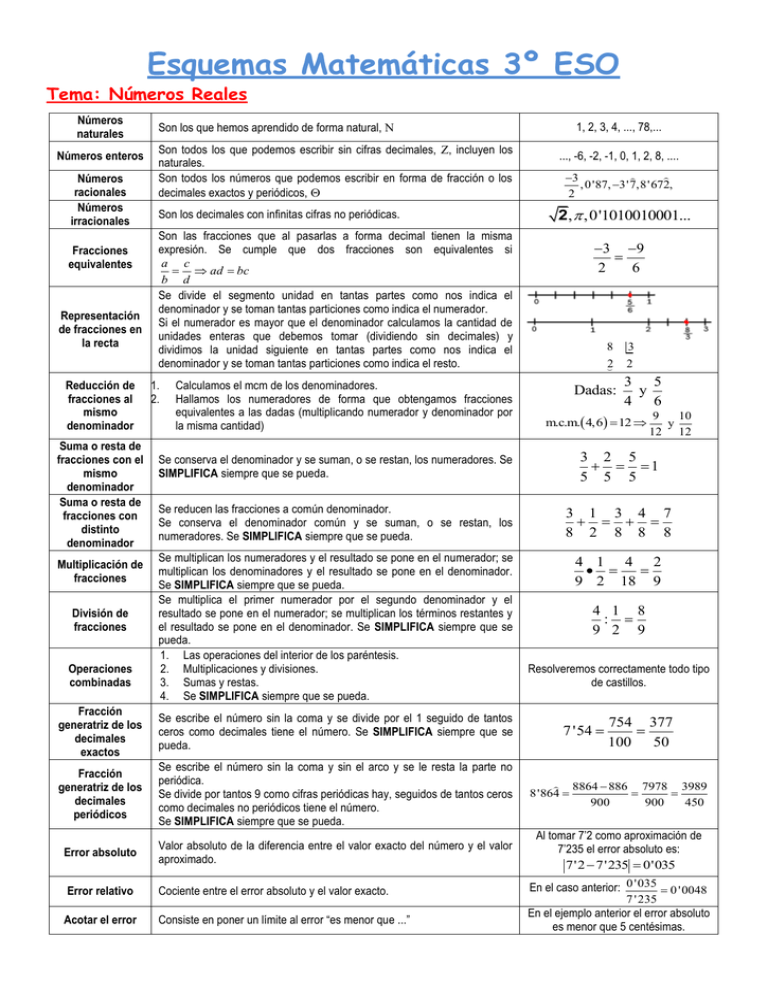
Esquemas Matemáticas 3º ESO
Tema: Números Reales
Números
naturales
Números enteros
Números
racionales
Números
irracionales
Fracciones
equivalentes
Representación
de fracciones en
la recta
Reducción de
fracciones al
mismo
denominador
Suma o resta de
fracciones con el
mismo
denominador
Suma o resta de
fracciones con
distinto
denominador
Multiplicación de
fracciones
División de
fracciones
Operaciones
combinadas
Son los que hemos aprendido de forma natural, 
Son todos los que podemos escribir sin cifras decimales, , incluyen los
naturales.
Son todos los números que podemos escribir en forma de fracción o los
decimales exactos y periódicos, 
Son los decimales con infinitas cifras no periódicas.
1, 2, 3, 4, ..., 78,...
..., -6, -2, -1, 0, 1, 2, 8, ....
3
, 0 '87, 3'7,8'672,
2
2,  ,0'1010010001...
Son las fracciones que al pasarlas a forma decimal tienen la misma
expresión. Se cumple que dos fracciones son equivalentes si
a c
  ad  bc
b d
Se divide el segmento unidad en tantas partes como nos indica el
denominador y se toman tantas particiones como indica el numerador.
Si el numerador es mayor que el denominador calculamos la cantidad de
unidades enteras que debemos tomar (dividiendo sin decimales) y
dividimos la unidad siguiente en tantas partes como nos indica el
denominador y se toman tantas particiones como indica el resto.
1.
2.
Calculamos el mcm de los denominadores.
Hallamos los numeradores de forma que obtengamos fracciones
equivalentes a las dadas (multiplicando numerador y denominador por
la misma cantidad)
3 9

2
6
8
3
2
2
Dadas:
3 5
y
4 6
m.c.m. 4,6  12 
9
10
y
12 12
Se conserva el denominador y se suman, o se restan, los numeradores. Se
SIMPLIFICA siempre que se pueda.
3 2 5
  1
5 5 5
Se reducen las fracciones a común denominador.
Se conserva el denominador común y se suman, o se restan, los
numeradores. Se SIMPLIFICA siempre que se pueda.
3 1 3 4 7
   
8 2 8 8 8
Se multiplican los numeradores y el resultado se pone en el numerador; se
multiplican los denominadores y el resultado se pone en el denominador.
Se SIMPLIFICA siempre que se pueda.
Se multiplica el primer numerador por el segundo denominador y el
resultado se pone en el numerador; se multiplican los términos restantes y
el resultado se pone en el denominador. Se SIMPLIFICA siempre que se
pueda.
1. Las operaciones del interior de los paréntesis.
2. Multiplicaciones y divisiones.
3. Sumas y restas.
4. Se SIMPLIFICA siempre que se pueda.
Fracción
generatriz de los
decimales
exactos
Se escribe el número sin la coma y se divide por el 1 seguido de tantos
ceros como decimales tiene el número. Se SIMPLIFICA siempre que se
pueda.
Fracción
generatriz de los
decimales
periódicos
Se escribe el número sin la coma y sin el arco y se le resta la parte no
periódica.
Se divide por tantos 9 como cifras periódicas hay, seguidos de tantos ceros
como decimales no periódicos tiene el número.
Se SIMPLIFICA siempre que se pueda.
Error absoluto
Valor absoluto de la diferencia entre el valor exacto del número y el valor
aproximado.
Error relativo
Cociente entre el error absoluto y el valor exacto.
Acotar el error
Consiste en poner un límite al error “es menor que ...”
4 1 4 2
 

9 2 18 9
4 1 8
: 
9 2 9
Resolveremos correctamente todo tipo
de castillos.
7 '54 
8'864 
754 377

100 50
8864  886 7978 3989


900
900
450
Al tomar 7’2 como aproximación de
7’235 el error absoluto es:
7'2  7'235  0'035
En el caso anterior: 0 '035  0 '0048
7 ' 235
En el ejemplo anterior el error absoluto
es menor que 5 centésimas.
Tema: Potencias y Raíces
Potencias
Producto de potencias con la
misma base
Se mantiene la base y se suman los exponentes
Cociente de potencias con la
misma base
Se mantiene la base y se restan los exponentes
32 : 33  323  31 
Potencia de una potencia
Se mantiene la base y se multiplican los exponentes
3 
Producto de potencias con el
mismo exponente
Se multiplican las bases y se mantiene el exponente
Cociente de potencias con el
mismo exponente
Se dividen las bases y se mantiene el exponente
Potencia de exponente cero
Si la base no es cero, es siempre 1 ( 00 es indeterminado)
Potencia de exponente negativo
2 3
Notación científica
Suma y resta en notación
científica
Debemos escribir todos los números que vamos sumar o
restar como números multiplicados por la misma potencia
de 10 (la de mayor exponente)
Sacamos factor común la potencia de 10 y sumamos o
restamos los números.
Al finalizar debemos comprobar que el resultado lo
escribimos correctamente en notación científica.
Multiplicamos los números y sumamos los exponentes de
las potencias de 10, o dividimos los números y restamos
los exponentes de las potencias de 10.
Al finalizar debemos comprobar que el resultado lo
escribimos correctamente en notación científica.
1
3
 323  36  729
22  32   2  3  62  36
2
2 : 3   2 : 3
2
2
2
2
 
3
2
30  1, 70  1
32 
Se escribe la fracción inversa con exponente positivo
Escribimos todas las cantidades como un número entre 1 y
10 (entero o decimal (en este caso se escribe una o dos
cifras decimales), positivo o negativo) multiplicado por una
potencia de 10 (con exponente positivo o negativo)
Multiplicación o división en
notación científica
32  33  323  35  243
1
32
9837475  9'83·106
0'0000005431  5'43·107
1'23·105  5'25·104  4 '03·106 
 0 '123·106  0 '0525·106  4 '03·106 
  0 '123  0 '0525  4 '03·106 
 3'85·106
1'23·105 ·5'25·104 6 '4575·109


4 '03·106
4 '03·106
 1'60235732·103  1'6·103
Raíces
Producto de raíces
a·b  a · b
25·100  2500  50
25·100  25· 100  5·10  50
a
a

b
b
100
 25  5
4
100
100 10

 5
4
2
4
Cociente de raíces
Suma o resta
Potencias con exponente
fraccionario (relación entre
potencias y raíces)
Solamente con radicales semejantes, es decir, mismo
índice y mismo radicando.
a x  b x   a  b x
3 3 5 3 6 3  2 3
Es igual a una raíz que tiene por índice el denominador de
la fracción y por radicando la misma base elevada al
2
2 3  3 22  3 4
z
numerador de la fracción.
a n  n az
4
4
81  4 34  34  3
Tema: Proporcionalidad
Razón
Proporción
Constante de
proporcionalidad
Entre dos números es el cociente, la razón entre a y b es a .
b
Es la igualdad entre dos o más razones. a  c
La razón entre 3 y 5 es:
Los números a y d se llaman
a c
 k
b d
Conocidos tres números a, b y c, se llama cuarto proporcional al número x que forma
Cuarto proporcional
proporción con ellos:
proporción con ellos:
Regla de tres simple
directa
Regla de tres simple
inversa
a b

b x
a x
  x 2  a·b  x  a·b
x b
Debemos estudiar cada una de las magnitudes, y mirar si forma proporcionalidad
directa o inversa, con la magnitud en la que tenemos la incógnita, x.
Porcentajes
Se trata siempre de reglas de tres simples directas:
Calcularemos el beneficio producido por un capital durante cierto tiempo colocado a un
interés simple. El capital final será la suma del capital inicial y el beneficio.
Interés compuesto
Calcularemos el capital al final que obtendremos por un capital colocado a un interés
compuesto.
Mezclas
a  b
b·c
x

a
c  x
a  b
a·b
x

c
c  x
Supongamos que tenemos:
D.
D.
I.
a  b  c  d
a'  b'  c'  x
a '·b '·c·d
x
a·b·c '
Porcentaje ahora  Euros? ahora


Porcentaje antes/después  Euros? antes/después
Interés simple
Repartos
inversamente
proporcionales
56
 14
4
El tercero proporcional de 10 y 20 es:
10 20

 10 x  20·20  400  x  10
20 x
El tercero proporcional de 20 y 10 es:
20 10
  20 x  10·10  100  x  5
10 x
El medio proporcional de 4 y 9 es:
4 x
  x 2  4·9  36  x  36  6
x 9
Dos magnitudes son directamente proporcionales si al aumentar una, aumenta la
otra, siguiendo una proporción.
Dadas dos magnitudes directamente proporcionales, tenemos que calcular un valor qué
falta.
Dos magnitudes son inversamente proporcionales si al aumentar una, la otra
disminuye, siguiendo una proporción.
Dadas dos magnitudes inversamente proporcionales, tenemos que calcular un valor
qué falta.
Regla de tres
compuesta
Repartos
directamente
proporcionales
4 8
  4 x  7·8  56
7 x
x
Dados dos números a y b, se llama medio proporcional al número x que cumple
Medio proporcional
6 12 60
 
3
2 4 20
La constante de proporcionalidad es 3.
El cuarto proporcional de 4, 7 y 8
es x tal que:
a c

b x
Si los medios son iguales, se llama tercero proporcional al número x que forma
Tercero proporcional
3 9 30
 
 ...
5 15 50
b d
extremos, los números b y c se llaman medios.
Es el valor del cociente entre a y b, o entre c y d.
3
5
I
C· interés ·t C·r·t

100
100
 interés 
C f  Ci ·1 

100 

t
Para repartir un número C en partes directamente proporcionales a varios números, a, b
t C
a·C
y c:
 xa 
,...

Se calcula la suma de los números a  b  c  t y se calculan los repartos usando las
a  xa
t

reglas de tres simples.
Para repartir un número C en partes inversamente proporcionales a varios números, a, b y c: Se toman los números: 1 , 1 , 1 , los
a b c
reducimos a común denominador, y se realiza el reparto directamente proporcional a los numeradores obtenidos.
Colocamos en la tabla los datos del problema.
kilos
€/kg
€ total
Además sabemos que el precio total de un producto es igual a la
Elaboraremos una
cantidad de producto (kg) multiplicada por el precio de cada kg.
Prod1
tabla similar a la
También sabemos que la cantidad de producto mezcla es igual a la
Prod2
siguiente:
suma de las cantidades de producto (kg) y que el precio total de la
Mezcla
mezcla es la suma de los precios totales de todos los productos que
mezclamos.
Para resolver estos problemas usamos siempre la fórmula v  e .
t
Móviles
Si se trata de un problema de encuentro (sentido contrario) usaremos v  vA  vB , si se trata de un problema de alcance (mismo
sentido) usaremos v  vA  vB
Si uno de los móviles sale antes que el otro, debemos calcular primero la distancia que recorre.
Tema: Expresiones algebraicas
Expresión
algebraica
Monomio
Grado de un
monomio
Es toda combinación de números y letras unidos por los signos de
las operaciones aritméticas: suma, resta, multiplicación y división
Es una expresión algebraica en la que tenemos la multiplicación
como única operación (y la potenciación con exponente natural)
Suele estar formado por un número (coeficiente) y alguna letra
(parte literal).
Cantidad total de letras que tiene, contando sus multiplicidades.
Es decir la suma de los exponentes de todas las letras.
Variables
Cada una de las letras que forman parte de una expresión
algebraica.
Monomios
semejantes
Binomio
Son los que tienen la parte literal igual (las mismas letras con los
mismos grados)
Suma o resta de dos monomios
Trinomio
Suma o resta de tres monomios
Polinomio
Suma o resta de varios monomios (2, 3, 4, 5, ...)
Término (en un
polinomio)
Grado de un
polinomio
Término principal
Término
independiente
Valor numérico
Polinomio
ordenado
Polinomio
completo
Polinomio
opuesto
3x 4  6 x 2  4 x  6
5x4 ,
6 xy5 z 4 tiene tres variables
que son x, y, z
3x2 h,
Es el resultado de sustituir cada variable por números y realizar
las operaciones.
5x 4  3'76 x 2 h Está
formado por 2 términos.
5 x 4  3'76 x 2 h Tiene
 4  3
grado 4
5 x 4  36 x 2  6 x  4 El término principal
es  5 x 4 , el coeficiente principal es -5.
5x4  36 x 2  6 x  4 El
término independiente es 4
p  x   x  2 x  4 Valor numérico
2
para x  3 : p  3  32  2·3  4  9  6  4  7
Sus términos van de mayor a menor grado, o viceversa.
5x4  36 x2  6 x  4
Tiene términos de todos los grados inferiores al mayor.
5x 4  2 x3  6 x 2  6 x  4
Se obtiene cambiando todos los signos de sus términos.
5x4  36 x2  6 x  4 y 5x 4  36 x 2  6 x  4
Suma (resta) de
monomios
Para poder sumar (restar) dos monomios deben ser semejantes.
Se suman (restan) los coeficientes y se mantiene la misma parte
literal.
Suma de
polinomios
Es un nuevo polinomio formado por la suma de los monomios
semejantes y los términos no semejantes de ambos.
Resta de
polinomios
Se suma el minuendo con el opuesto del sustraendo.
Producto de
monomios
Es un monomio con coeficiente el producto de los coeficientes y
como parte literal el producto de las letras (si tenemos la misma
variable se suman los exponentes)
3x2h  9x2h   3  9 x2h  6x2h
3x2h  9x2h   3  9 x2h  12x2h
3x3  6 x  2
x2  5x  7
3
3x  x 2  x  5
3
3x  6 x  2
3x3  6 x  2
 2
 2
x  5x  7
 x  5x  7
 3 2
3x  x  11x  9

3x3 y·6xz 2  18x4 yz 2

Producto de
polinomios
9x2 h
5x 4  3'76 x 2 h
5x 4  3'76 x 2  7 x
5x4  36 x2  6 x  4
El mayor de los grados de los términos que forman el polinomio.
Es el término de grado 0, el que no tiene letras.
Se multiplica cada monomio de un factor por todos los monomios
del otro factor.
3x3  6 x  2
x2  7
21x  42 x  14
3
3x5  6 x3  2 x 2
3 x  27 x 3  2 x 2  42 x  14
5
División de
monomios
6xy5 z 4
6xy5 z 4 tiene grado 10
Cada uno de los monomios que forman parte de un polinomio se
llama término.
Es el término de mayor grado en un polinomio. Su coeficiente es
el coeficiente principal.
3'76x2h,
Se dividen los coeficientes y se restan los exponentes de las
variables.
9 x 7 : 3x 2  3x5
División de
polinomios
Igualdades
notables
Raíz de un
polinomio
Se divide el término principal del dividendo entre el término
principal del divisor, el monomio resultante se escribe en el
cociente. Se multiplica este monomio por el divisor y se escribe
debajo del dividendo el opuesto del resultado. Sumamos esto con
el dividendo y obtenemos un resto provisional.
Repetimos el proceso hasta que este resto provisional tiene grado
menor que el divisor.
x 4  3x3  5 x 2  4 x  2
x2  5x 1
Dividendo
 x  5x  x
2 x3  4 x 2  4 x
2 x3  10 x 2  2 x
4
3
Divisor
x2  2 x  6
2
Cociente
6x2  2x  2
6 x 2  30 x  6
Resto  28 x  4
 2 x  5
Cuadrado de una suma  a  b 2  a 2  b 2  2ab
 4x
Cuadrado de una resta  a  b 2  a 2  b 2  2ab
Suma por diferencia  a  b· a  b  a2  b2
 3x
Es un valor de la indeterminada que hace cero el polinomio.
2
2
2
  2 x   52  2·2 x·5
2
 1   4 x 2   12  2·4 x 2 ·1
2
2
 2 x · 3x 2  2 x    3x 2    2 x 
2
2
Una raíz de 3x2  4 x  20 es x  2
Tema: Ecuaciones
Formadas
por:
Igualdades,
expresiones con un
signo =
Ecuación de
primer grado
(lineales)
Ecuación de una
incógnita
Regla de la suma
Regla del
producto
Ecuaciones de
primer grado y
una incógnita
Ecuaciones de
segundo grado y
una incógnita
Tipo b=0, a=0
Tipo b=0
Según sea
cierta o no:
34  20  14
Números y operaciones. Numérica
Números, letras y operaciones. Algebraica
Identidad: Siempre es cierta
Contradicción, absurdo o incompatible:
nunca es cierta
Ecuación: Se cumple solo para ciertos
valores de las letras. Resolver una ecuación
consiste en averiguar para qué valores de las
letras se cumple la igualdad.
3x2  4 x  20  2
53  2,
57  2
3x 2  4 x  2
Igualdad formada por números y letras, de forma que en
ningún caso las letras están multiplicadas o divididas entre sí.
3x  4 y  20 x  2
Igualdad formada por números y una sola letra, que puede
aparecer en forma de potencia.
3x2  4 x  20  2
4 x  20  2 x  10 
4 x  2 x  20  2 x  2 x  10 
2 x  20  10
Si a los dos miembros de una ecuación sumamos o restamos
la misma cantidad, obtenemos una ecuación equivalente.
Si los dos miembros de una ecuación los multiplicamos o
4 x  22 2
4 x  22  2 

dividimos por la misma cantidad distinta de cero, obtenemos
4
4
una ecuación equivalente.
Son las igualdades que se pueden escribir como ax  b  0 ,
x
x4
 1
,
m.c.m.  4, 6   12
con a  0 , el valor de x que verifica la igualdad es la solución
4
6
de la ecuación.
1. Mínimo común múltiplo de denominadores, y se 12 x  12  12  x  4   3 x  12  2  x  4  
4
6
multiplican todos los términos por esa cantidad.
2. Se suprimen paréntesis aplicando la propiedad 3x  12  2 x  8  3 x  20  2 x 
distributiva y cambiando todo de signo si tenemos
20
3 x  2 x  20  2 x  2 x  5 x  20  x 
x4
delante un signo “-“
5
3. Se aplican las reglas de la suma y el producto.
Son las igualdades que se pueden escribir como
ax2  bx  c  0 , con a  0 , los valores de x que verifican la
3x2  4 x  20  2
igualdad son las soluciones de la ecuación.
Ecuaciones de segundo grado incompletas
ax2  0,despejamos x  x2  0,  x  0
3x2  0,  x  0
 6x2  0,  x  0
c
c
, x 
a
a
ax 2  bx  0,sacamos x factor común  x  ax  b   0
ax 2  c  0,  ax 2  c,  x 2 
3x 2  48  0,  3 x 2  48,  x 2 
tenemos un producto igualado a cero, luego, cada uno de
Tipo a=0
5 x  3x  2 x
los factores debe ser cero,  x  0 y ax  b  0,
b
a
Ecuaciones de segundo grado completas
luego las soluciones son,  x  0 y x 
48
=16,  x  4
3
5 x 2  15 x  0,  x  5 x  15  0
 x  0 y 5x  15  0,
15
x0 y x
 3
5
3 x 2  x  2  0,  a  3, b  1, c  2
Las soluciones de una ecuación ax2  bx  c  0, de segundo grado
1  12  4·3· 2 
1  1  24


2·3
6
1  5 4
2

x
 x

1  5

6
6
3
x


1

5

6
6
x 

 x  1

6
6

Si b2  4ac  0 la ecuación no tiene Si b2  4ac  0 la ecuación tiene una solución Si b2  4ac  0 la ecuación tiene dos
solución.
(doble)
soluciones.
2
Si x1 , x2 son las dos soluciones de la ecuación ax  bx  c  0, se cumple: x1  x2  b , x1 ·x2  c
a
a
b  b  4ac . Llamaremos
completa vienen dadas por
x
2a
discriminante a: b2  4ac su valor de positividad permite saber el
número de soluciones sin resolver la ecuación.
2
x
Tema: Sistemas
Ecuación lineal con dos
incógnitas
Sistema de dos
ecuaciones lineales y
dos incógnitas
Son las ecuaciones de primer grado, que tienen dos incógnitas, de la
forma ax  by  c , cualquier par de valores,  x, y  que verifique la
igualdad es una solución de esta ecuación. Si las representamos
gráficamente, obtenemos una recta.
x  3 y  2 Son soluciones:
 5,1 , 1, 1 ,  4, 2  ,...
ax  by  c
Se trata de calcular los valores  x, y  de las incógnitas para los
a ' x  b ' y  c '
Se suele representar 
cuales se cumplen las dos ecuaciones.
No existe ningún par de valores  x, y  para los cuales se cumpla el
Sistema incompatible
sistema. Si representamos las dos rectas vemos que son paralelas.
a b c
 
a' b' c'
Existe un único par de valores
Sistema compatible
determinado
 x, y 
para los cuales se cumple el
sistema. Si representamos las dos rectas vemos que son secantes.
a b

a' b'
Existen infinitos pares de valores  x, y  para los cuales se cumple el
Sistema compatible
indeterminado
sistema. Si representamos las dos rectas vemos que son coincidentes,
a b c
 
son la misma.
a' b' c'
Igualación
Se basa en despejar la misma incógnita en
las dos ecuaciones e igualar las
expresiones resultantes. El valor encontrado
para la primera incógnita se sustituye en
cualquiera de las ecuaciones que forman el
sistema para hallar la otra incógnita.
x  2 y  7

 x  2 y  4
Métodos de resolución de sistemas
Sustitución
Consiste en despejar una incógnita en una
ecuación y sustituirla en la otra. El valor
encontrado para la primera incógnita se
sustituye en cualquiera de las ecuaciones
del sistema y se halla el valor de la otra.
x  2 y  6
  2, 2 

2 x  y  2
2 x  y  3

4 x  2 y  6
Reducción
Se trata de conseguir que las ecuaciones
tengan coeficientes opuestos para una
misma incógnita; así, al sumar ambas
ecuaciones se obtiene una única ecuación
con una sola incógnita que se resuelve. El
valor hallado se sustituye en cualquiera de
las ecuaciones del sistema para hallar la
segunda incógnita.
7  5y

x
3 x  5 y  7 3 x  7  5 y 
3




2x  6 y  1 2x  1  6 y  x  1 6 y

2
7  5y 1 6 y

 2  7  5 y   3 1  6 y  
3
2
14  10 y  3  18 y  18 y  10 y  3  14 
11
8
Volvemos a una de las ecuaciones que
8 y  11  y 
tenemos despejadas y sustituímos el valor
calculado, para calcular el valor de la
otra incógnita:
 11 
66
33 37
1 6
1
 1
8 

8
4  4  37
x


2
2
2
2
8
37
11
El sistema tiene solución: x  , y 
8
8
10  x  2   y  1 10 x  20  y  1



 x  3  x  y   5
 x  3x  3 y  5
10 x  y  1  20 10 x  y  21


3x  4 y  9 3 x  4 y  9
 4x  3y  5

 Sustituímos:  4 x  3 y  5

 2x  y  5
 y  5  2x
Multiplico la primera ecuación por "3" para
 3x  4  5  2 x   9  3 x  20  8 x  9
obtener en "y" coeficientes iguales, con
11
signos
distintos:
 3x  8 x  9  20  11x  11  x   1
11
30 x  3 y  63
 Sumamos las ecuaciones:

Volvemos al principio, dónde teníamos "y"
 4x  3y  5
despejada, cambiamos "x" por su valor, y
68
 34 x  68  x 
2
calculamos el valor de "y":
34
y  5  2 x  5  2·1  5  2  3
Volvemos a una ecuación y sustituimos
El sistema tiene solución: x  1, y  3
el valor obtenido: 4 x  3 y  5  4·2  3 y  5
 8  3 y  5  3 y  5  8  3  y 
3
1
3
El sistema tiene solución: x  2, y  1
Tema: Sucesiones
Sucesiones
Progresiones
aritméticas
Término general
Una sucesión es una colección de números dados
ordenadamente, que siguen una pauta.
Son sucesiones en las que se pasa de cada término al siguiente
sumando una cantidad fija que llamaremos diferencia, d.
Es la expresión matemática que nos da el valor de un término en
función del primer término de la sucesión y del lugar que ocupa.
an  a1   n 1·d
Ejemplo: 6, 9, 12...
1, 4, 7, 10, 13, 16,... (d=3)
En el ejemplo anterior
an  1  n 1·3  1 3n  3  an  3n  2
En el ejemplo anterior Sn 
Suma de los n
primeros términos
Sn 
 a1  an ·n
2
Término general
(Debemos conocer el último término que
vamos a sumar, y el tipo de sucesión que es)
Son sucesiones en las que se pasa de cada término al siguiente
multiplicando por una cantidad fija que llamaremos razón, r.
Es la expresión matemática que nos da el valor de un término en
función del primer término de la sucesión y del lugar que ocupa.
an  a1·r
2
La suma de los 4 primeros términos
S4 
S4 
Progresiones
geométricas
1  (3n  2)·n
n1
1  (3·4  2)·4 
2
1  10·4
2
 S4  22
2, 6, 18, 54, 162,... (r=3)
n1
En el ejemplo anterior an  2·3
En el ejemplo anterior
Suma de los n
primeros términos
Suma de todos los
términos
Sn 
a1  an ·r
a ·r  a1
o bien Sn  n
(cualquiera) (Debemos
1 r
r 1
conocer el último término que vamos a sumar, y el tipo de
sucesión que es)
Sólo se puede hacer en el caso 0  r  1 , en ese caso
S
a1
1 r
Sn 
2·3n1·3  2 2·3n  2

3 1
2
La suma de los 4 primeros términos
2·34  2 2·81  2


2
2
162  2 160
Sn 

 80
2
2
1 1 1  1
Ej: 4, 2, 1, , , ,...  r  
2 4 8  2
4
4
S
= 8
1 1
1
2 2
Sn 