0.0.1 Ecuacion de Van der Walls Habiamos visto que una posible

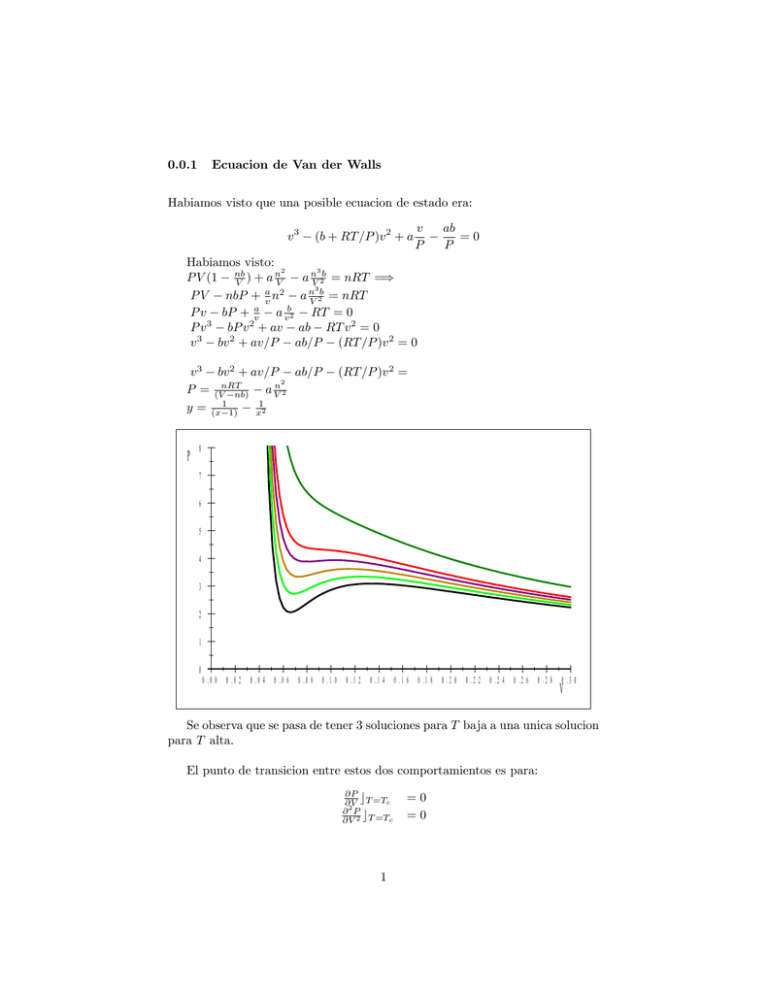
0.0.1
Ecuacion de Van der Walls
Habiamos visto que una posible ecuacion de estado era:
v3
(b + RT =P )v 2 + a
v
P
ab
=0
P
Habiamos visto:
3
n2
a nV 2b = nRT =)
P V (1 nb
V )+aV
3
P V nbP + av n2 a nV 2b = nRT
P v bP + av a vb2 RT = 0
P v 3 bP v 2 + av ab RT v 2 = 0
v 3 bv 2 + av=P ab=P (RT =P )v 2 = 0
v 3 bv 2 + av=P ab=P
2
P = (VnRT
a Vn 2
nb)
y = (x 1 1) x12
P
(RT =P )v 2 =
8
7
6
5
4
3
2
1
0
0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 0.20 0.22 0.24 0.26 0.28 0.30
V
Se observa que se pasa de tener 3 soluciones para T baja a una unica solucion
para T alta.
El punto de transicion entre estos dos comportamientos es para:
@P
cT =Tc
@V
@2P
@V 2 cT =Tc
1
=0
=0
Para la primera derivada
a
2
c
P = RT
v b
v 2 =) v 3 a =
n
o
2
Tc = R2 va3 ( b + v)
RTc
(v b)2
la segunda derivada es v64 a + 2 (vRTb)c 3 = 0
n
o
3
de donde Tc = R3 va4 ( b + v) =)
o
n
2
)
Tc = R2 va3 ( b + v) ( 23 ( b+v)
v
Se debe cumplir ( 32 ( b+v)
)=1
v
de donde vc = 3b
Ahoran se obtiene
o
2
a
8 a
Tc = R2 (3b)
b + 3b) = 27R
3 (
b
de donde
8 a
R( 27R
b)
1
1 a
a (3b)
Pc = ((3b)
2 = 27 b2
b)
Luego Van der Waals se puede escribir
P+
donde T =
0.0.2
T
Tc ;
3
v2
(3v
1) = 8T
etc.
Comportamiento extraµno de P
Por la condicion de estabilidad mecanica las funciones respuesta tienen signos
de…nidos
T >0
CV > 0
etc.
1 @V
T =
V @P
2
P
8
6
4
2
0
0
0.05
0.1
0.15
0.2
0.25
0.3
V
Aqui podemos ver 3 regiones
i) V < Va
ii) Va < V < Vb
iii)Vb < V
Que ocurre en cada region
i) @V
@P < 0 =) T > 0
iii)
@V
@P
< 0 =)
T
ii)
@V
@P
> 0 =)
T
<0
>0
Luego el comportamiento de la ecuacion de VdW en ii) es imposible.
Para resolver esta inconsitencia usamos G
G = U T S XY
dG
SdT XdY
Como trabajamos sobre la isoterma en equilibrio (molar)
dg = vdP
RP
entonces g = P12 v(P )dP
3
P
5
3.75
2.5
1.25
0
0
0.2
0.4
0.6
0.8
V
Si integramos sobre la curva (ojo con los ejes) obtendremos
[aqui …gura]
4
Para determinar los puntos C y G hacemos
0=
Z
PG
v(P )dP
PC
de donde
Z
PD
v(P )dP +
Z
PE
v(P )dP +
PF
v(P )dP +
Z
PG
v(P )dP = 0
PF
PE
PD
PC
Z
Entonces
Z
PD
v(P )dP
PC
Z
PD
v(P )dP =
PE
Z
PE
PF
Areas Iguales !!!!!!
5
v(P )dP
Z
PG
PF
v(P )dP
P
8
6
4
2
0
0
0.05
0.1
0.15
0.2
0.25
0.3
V
6