Problemario Benjamín 2007

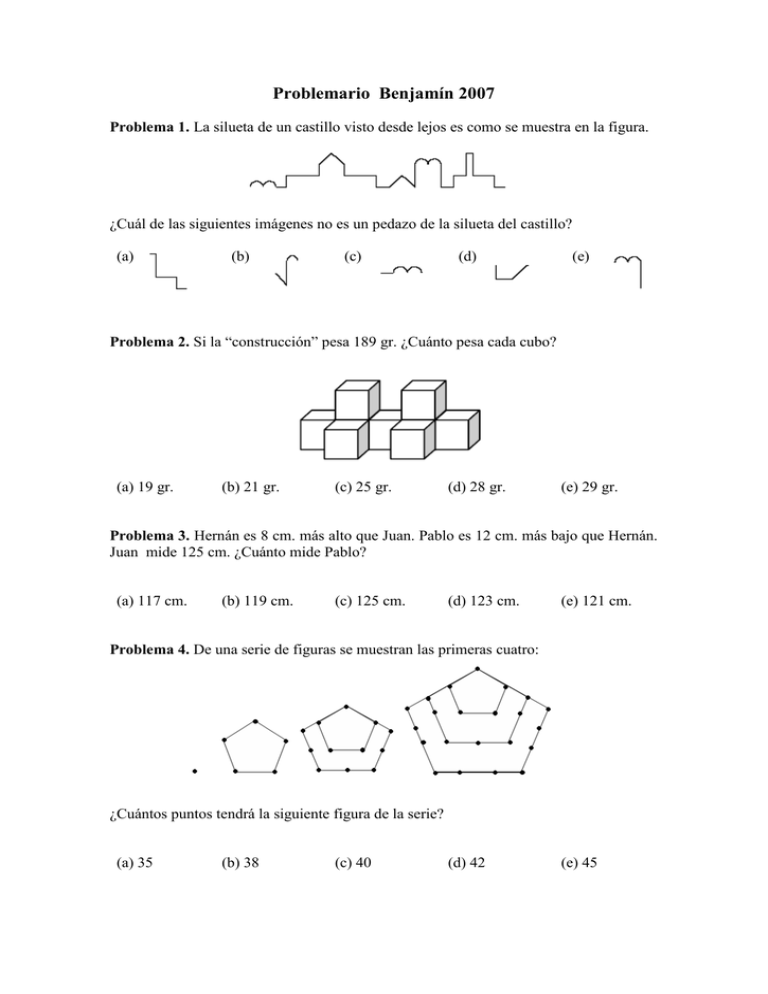
Problemario Benjamín 2007
Problema 1. La silueta de un castillo visto desde lejos es como se muestra en la figura.
¿Cuál de las siguientes imágenes no es un pedazo de la silueta del castillo?
(a)
(b)
(c)
(d)
(e)
Problema 2. Si la “construcción” pesa 189 gr. ¿Cuánto pesa cada cubo?
(a) 19 gr.
(b) 21 gr.
(c) 25 gr.
(d) 28 gr.
(e) 29 gr.
Problema 3. Hernán es 8 cm. más alto que Juan. Pablo es 12 cm. más bajo que Hernán.
Juan mide 125 cm. ¿Cuánto mide Pablo?
(a) 117 cm.
(b) 119 cm.
(c) 125 cm.
(d) 123 cm.
(e) 121 cm.
Problema 4. De una serie de figuras se muestran las primeras cuatro:
¿Cuántos puntos tendrá la siguiente figura de la serie?
(a) 35
(b) 38
(c) 40
(d) 42
(e) 45
Problema 5. Cuando son las nueve de la noche, ¿qué fracción del día ha transcurrido?
(a)
3
4
(b)
7
8
(c)
3
8
(d)
7
24
(e)
1
8
Problema 6. Añadiendo 17 al menor de los números de dos dígitos y dividiendo esta
suma entre el mayor de los números de un dígito se obtiene:
(a) 3
(b) 6
(c) 9
(d) 11
(e) 27
Problema 7. ¿Cuál es el área de la figura sombreada si cada lado del cuadrado mide x?
x
2
x
2
(a) x 2 
x2
4
(b) x 2 
 x2
8
(c)
 x2
(d) x 2  2
(e) x 2 
8

2
Problema 8. Pablo y Gabriel son dos amigos que viven en el país de los mentirosos.
Pablo miente los lunes, martes y miércoles, y Gabriel miente los jueves, viernes y
sábados. En todas las demás ocasiones ambos dicen la verdad. Un día Pablo le dijo a
Gabriel: Ayer me tocó mentir, a lo que Gabriel le contestó: También a mí me tocó
mentir. ¿En qué día de la semana estaban?
(a) martes
(b) viernes
(c) miércoles
(d) lunes
(e) jueves
Problema 9. Se tiene una asignación entre los números como sigue: al uno le
corresponde el 3, al dos le corresponde el 3, al cuatro le corresponde el 6, al cinco le
corresponde el 5, al seis le corresponde el 4, al siete le corresponde el 5 y al ocho le
corresponde el 4, ¿qué número le corresponde al nueve?
(a) 3
(b) 4
(c) 5
(d) 6
(e) 7
Problema 10. Globito, Bizcochito y la galletita Sol fueron a una fiesta donde comieron
pizza y decidieron ver quién podía comer más pedazos.
La galleta Conquistador recuerda que la galletita Sol comió dos pedazos más que cinco
veces la mitad de lo que comió Bizcochito. Además, si a lo que comió la galletita Sol le
sumamos cuatro veces lo que comió Bizcochito obtenemos el total de lo que comió
Globito. Todos se sorprendieron al ver que Globito comió siete veces lo que comió
Bizcochito. ¿Cuántos pedazos comió la galletita Sol?
(a) 8 pedazos
(b) 10 pedazos
(c) 7 pedazos
(d) 12 pedazos
(e) 13 pedazos
Problema 11. ¿Cuál es el residuo de dividir el número 12345678987654321 entre 9?
(a) 0
(b) 1
(c) 3
(d) 5
(e) 7
Problema 12. La mamá de Drini tiene una sartén donde sólo caben dos hot-cakes y
cada lado necesita una cocción de un minuto. ¿Cuál será el menor tiempo posible para
que la mamá de Drini pueda cocer 3 hot-cakes?
(a) 6 minutos
(b) 5 minutos
(c) 4 minutos
(d) 3 minutos
(e) 2 minutos
Problema 13. El cuerpo que se ilustra a continuación está formado por cubos iguales.
Si cada cubito pesa 2.5 gr., ¿cuánto pesa el cuerpo?
(a) 108 gr.
(b) 165 gr.
(c) 210 gr.
(d) 225 gr.
(e) 245 gr.
Problema 14. Un semáforo tarda 45 segundos en verde, 4 segundos en amarillo y 30
segundos en rojo, siguiendo ese orden. Si a las 7:00 a.m. el semáforo cambia a verde,
¿de qué color estará a las 2:34 p.m.?
(a) verde
(b) amarillo
(c) rojo
(d) cambia de rojo (e) cambia de verde a
a verde
amarillo
Problema 15. En la siguiente figura, los segmentos unen los vértices de un cuadrado de
área 1 cm2 con los puntos medios de sus lados. ¿Cuál es el área del cuadrado que se
forma en el centro?
a)
1
cm2
5
(b)
1
cm2
6
(c)
1
cm2
8
(d)
1
cm2
4
(e)
1
cm2
7
Problema 16. ¿Cuántas caras tiene la figura siguiente?
(a) 12
(b) 14
(c) 16
(d) 20
(e) 22
(d) 3 Kg.
(e) 6 Kg.
Problema 17. Observa las balanzas:
¿Cuánto pesa el envase vacío?
(a) 1 Kg.
(b) 4 Kg.
(c) 2 Kg.
Problema 18. ¿Qué dígito representa A en la suma de A000 + A998 + A999 = 22997?
(a) 0
(b) 1
(c) 5
(d) 7
(e) 8
Problema 19. ¿Cuál es el término siguiente de la serie: 1, 3, 5, 11, 21,…?
(a) 41
(b) 43
(c) 44
(d) 40
(e) 42
Problema 20. En algunos de los cuadrados pequeños de una cuadrícula de 2 x 9 hay
monedas. Cada cuadrado pequeño contiene una moneda o tiene un lado común con un
cuadrado semejante que contiene una moneda. De entre las siguientes opciones, ¿cuál es
el menor número de monedas que puede haber en la cuadrícula de manera que sí cumpla
con las condiciones del enunciado?
(a) 5 monedas
(b) 6 monedas
(c) 7 monedas
(d) 8 monedas
(e) 9 monedas
Problema 21. Tres cuadrados cuyos lados miden 10 cm., 8 cm. y 6 cm.
respectivamente, se colocan uno al lado del otro como se muestra en la figura:
¿Cuál es el área de la parte sombreada?
(a) 60 cm2.
(b) 120 cm2.
(c) 80 cm2.
(d) 70 cm2.
(e) 100 cm2.
Problema 22. Coloca en los recuadros los dígitos 5, 4, 7, 1, 3, sin que se repitan, de tal
forma que al restar obtengas la menor diferencia posible. ¿Cuál es esta diferencia?
(a) 45
(b) 59
(c) 31
(d) 63
(e) 23
Problema 23. Se tienen muchos dominós y cuatriminós lineales y se ordenan, de arriba
hacia abajo, de la siguiente manera: dos dominós al principio, luego alternadamente un
cuatriminó y un dominó y se les escriben números como se ilustra acontinuación:
Si continuamos enumerando de esta forma, ¿en qué lugar se ubica el número 2006?
(a)En un (b)En
un (c)
En
un (d)
En
un (e)En
un
dominó en cuatriminó en cuatriminó en la 3ª cuatriminó en la dominó en la
la
2ª la 2ª posición posición
4ª posición
1ª posición
posición
Problema 24. Marcamos un punto en el suelo con la letra A. A la tapa de una botella
que tiene un diámetro de 4 centímetros se le han dibujado dos diámetros: Bb y Cc,
perpendiculares entre sí, como se muestran en las figuras 1 y 2. Inicialmente la b de la
tapa toca al suelo en A (Fig. 1). Luego, la tapa da un cuarto de vuelta hacia la derecha y
ahora C toca al suelo (Fig. 2). ¿Cuál es el área del triángulo ABC que se forma en la
figura 2?
Fig. 1
B
Fig. 2
c
C
c
(a) 2  cm2
(b)  cm2
b
b
(c) 
2 cm2
(d) 
A
1
cm2
2
A
B
(e) Ninguna de
las anteriores
C
Problema 25. Se construye un rompecabezas recortando un cuadrado de 1 cm. de lado
en cinco triángulos, un cuadrado y un paralelogramo como en la figura. ¿Cuál es el área
del paralelogramo?
1/2
(a)
1
cm2.
8
(b)
1
cm2.
16
(c)
1/2
1
cm2.
4
(d)
1
cm2.
32
(e)
1
cm2.
64
Problema 26. Dos números son tales que están en razón 2:5. Si uno de ellos es 21 más
que el otro, ¿cuáles son los números?
(a) –14, -35
(b) 15, 36
(c) 10, 25
(d) 100, 121
(e) 6, 15
Problema 27. ABCD es un cuadrado cuyo lado mide 4 cm. Si P, Q, R y S son los
puntos medios de los lados,
¿cuál es el área de la región
sombreada?
(a) 16 cm2.
(b) 12 cm2.
(c) 10 cm2.
(d) 9 cm2.
(e) 8 cm2.
Problema 28. En la figura siguiente, los lados del cuadrado pequeño son paralelos a los
del cuadrado grande. El área del cuadrado grande es 25 cm2 . y el área del cuadrado
chico es 9 cm2. ¿Cuál es el área del cuadrado mediano?
(a) 15.5 cm2.
(b) 16 cm2.
(c) 16.5 cm2.
(d) 17 cm2.
(e) 17.5 cm2.
Problema 29. Empezamos con una cuadrícula de 2 x 2 cuyas celdas están nombradas
con las letras a, b, c y d como se ilustra acontinuación:
a
b
c
d
Figura 1.
La operación 1 consiste en intercambiar las letras en cada diagonal y la operación 2
consiste en intercambiar las columnas. Ejemplo:
a
b
c
d
Op.1
d
c
b
a
Op.2
c
d
a
b
Empezando con la figura 1 y realizando 2006 operaciones alternadas, primero la
operación 1 y luego a la cuadrícula resultante aplicarle la operación 2 y así
sucesivamente, ¿qué letra queda al final en la celda inferior derecha?
(a) a
(b) b
(c) c
(d) d
(e)
No
se
puede saber
Problema 30. Gary el caracol decide subir un edificio comenzando desde el suelo. De
lunes a viernes sube 3 cm. cada día, pero sin darse cuenta se chorrea 1 cm. mientras
duerme por cada noche. Para descansar, se relaja los sábados y domingos durmiendo,
sólo que esto hace que se chorree 2 cm. por cada uno de estos días. Si comienza a subir
un jueves por la mañana, ¿cuánto habrá recorrido, en total, al final de la noche 2006?
(a) 2006 cm.
(b) 12120 cm.
(c) 12012 cm.
(d) 1716 cm.
(e) 1706 cm.
SOLUCIONES
Solución 1. Podemos observar que los pedazos (a), (b), (d) y (e) son parte del castillo,
por lo tanto la respuesta es (c).
Solución 2. La construcción tiene en total 9 cubos, por lo tanto cada cubo pesa
189 g.
 21g. La respuesta es (b).
9
Solución 3. Si Hernán es 8 cm más alto que Juan, Hernán mide 133 cm. Si Pablo es 12
cm más bajo que Hernán, Pablo mide 121 cm. La respuesta es (e).
Solución 4. La figura que sigue en la serie es la que se ilustra a continuación:
Entonces tiene 35 puntos. La respuesta es (a).
Solución 5. Solamente hay que notar que cada día tiene 24 horas y que las 9 de la noche
corresponde a las 21 horas de un día. Así, cuando son las nueve de la noche, la fracción
de un día es 21/24=7/8. La respuesta es (b).
Solución 6. El menor de los números de 2 dígitos es 10, sumando 17 a 10 obtenemos
27. El mayor de los números de un dígito es 9, por lo tanto dividiendo 27 entre 9
obtenemos 3. La respuesta es (a).
Solución 7. El área de la región sombreada será igual al área del cuadrado de lado x
x
menos el área de la mitad de un círculo de radio . Entonces el área será:
2
2
  x 
  x2 
    
  x2
    
 2 
  4 
  x2
 



2
2
2
2
4
x 
x 
x 
x 
2
2
2
8
La respuesta es (b).
Solución 8. Comencemos por observar que ambos dicen la verdad el domingo, así que
Pablo no puede decir el domingo que mintió el sábado, pues el sábado también dijo la
verdad.
El lunes Gabriel no puede decir que mintió el domingo, pues el lunes dice la verdad. De
la misma manera, vemos que Gabriel no pudo decir que mintió el día anterior al martes
o miércoles.
Similarmente, Pablo no puede decir que mintió un día antes del viernes o sábado.
Queda solamente el jueves, día en el que Gabriel puede mentir y decir que mintió el
miércoles, y Pablo puede decir la verdad acerca de que mintió el miércoles.
El día en que Pablo dice la verdad y Gabriel miente es el jueves. La respuesta es (e).
Solución 9. Notemos que la palabra uno tiene tres letras, la palabra dos tiene tres letras,
la palabra cuatro tiene seis letras, etc. La asignación corresponde a la cantidad de letras
que tiene la palabra. Como nueve tiene 5 letras le corresponde el 5. La respuesta es (c).
Solución 10. Si n es la cantidad de pedazos que comió Bizcochito, entonces la galletita
 5

 5

Sol comió  n  2  pedazos y Globito comió 4n   n  2  pedazos; pero también se
 2

 2

dijo que Globito comió 7 n pedazos de pizza, entonces tenemos que resolver la igualdad
 5

4n   n  2  = 7 n , de donde obtenemos que n  4 . Sustituyendo el valor de n en la
 2

 5

expresión  n  2  obtendremos lo que comió la galletita Sol, así tenemos que ésta
 2

comió 12 pedazos de pizza. La respuesta es (d).
Solución 11. Utilizando el criterio de divisibilidad del nueve, tenemos que el residuo de
dividir un número entre 9 es el mismo que el residuo de dividir la suma de los dígitos
del número entre 9, por ejemplo, al dividir 1001 entre 9 el residuo es 2, y la suma de los
dígitos es 1+0+0+1 = 2. Si consideramos el número 769, vemos que al dividirlo por 9
queda el residuo 4, mientras que la suma de sus dígitos es 7+6+9 = 22, lo que al
dividirse entre 9 deja como residuo 4. Así, calculamos la suma
1+2+3+4+5+6+7+8+9+8+7+6+5+4+3+2+1 = 81, y notamos que 81 deja residuo 0 al
dividirse por 9, así que el número 12345678987654321 deja residuo 0 al dividirse por 9.
La respuesta es (a).
Solución 12. Si le llamamos A, B y C a los tres hot-cakes, la mamá de Drini se tardará
tres minutos para cocerlos en el siguiente orden: Primero pone un lado de A y un lado
de B para cocer. Cuando ya estén cocidos esos lados habrá pasado el primer minuto.
Luego saca de la sartén a A, pone el otro lado de B y pone en la sartén un lado de C.
Cuando pase el segundo minuto el hot-cake B ya estará cocido y tanto A como C tienen
un lado cocido. Poniendo en la sartén los lados de A y C que faltan por cocer se
termina, tomando en total 3 minutos. La respuesta es (d).
Solución 13. La figura representa un paralelepípedo formado por cubos al que le hemos
quitado algunos cubos. Una manera de resolverlo es observando que el paralelepípedo
consta de 6 cubos en la base, 6 cubos de altura y 3 de profundidad, por tanto este objeto
tiene 6x6x3=108 cubos. Pero nuestra figura no contiene dos filas (en la parte de arriba)
de 1x3 cubos, así como tampoco contiene dos filas de base y dos de alto por 3 de
profundidad en el centro, es decir, 2x2x3 cubos.
Entonces nuestra figura consta de 108-2(1x3)-2x2x3=90 cubos. Como cada uno de ellos
pesa 2.5 gr. entonces el cuerpo pesa 90x2.5 gr.= 225 gr. Por tanto, la respuesta es (d).
Otra manera de contar los cubos de la figura es observando que si quitamos la parte
superior de cubos podemos rellenar el hueco para obtener un paralelepípedo de
6x5x3 =90 cubitos.
Solución 14. Al momento de que el semáforo cambia a verde, tienen que transcurrir 79
segundos para que esto vuelva a ocurrir. Si el semáforo cambia a verde a las 7 en punto,
entonces han pasado 7 horas 34 minutos cuando den las 2:34 p.m. Convirtiendo en
segundos tenemos 7(3600) + 34(60) = 27240 segundos trascurridos. Dividiendo entre
79 vemos que han pasado 344 ciclos de 79 segundos y aún sobran 64 segundos, si a
éstos les quitamos los 45 segundos que tarda el verde y los 4 que tarda el amarillo nos
quedan 15 segundos, por lo tanto el semáforo está en rojo. La respuesta es (c)
Solución 15. Como trazo auxiliar, dupliquemos la figura para obtener:
Esto nos permite ver que cada triángulo rectángulo chico junto con un trapecio forman
un cuadrado congruente con el del centro, por ejemplo los etiquetados con la letra A.
Veamos que esta afirmación es cierta: la hipotenusa del triángulo A mide 0.5 cm. al
igual que el lado inclinado del trapecio, además, el lado del trapecio y del cuadrado
miden lo mismo que un cateto del triángulo, pues los segmentos son determinados por
rectas paralelas. Además, por semejanza de triángulos podemos afirmar que el cateto
menor mide la mitad del cateto mayor.
Si ahora etiquetamos la figura original como sigue:
entonces obtenemos cuatro cuadrados formados con las etiquetas A, B, C y D, todos
ellos congruentes al cuadrado del centro.
Puesto que la suma de las áreas de cada uno de estos cuadrados debe de ser igual al
área del cuadrado grande, el área del cuadrado del centro es un quinto del área del
cuadrado grande. La respuesta es (a).
Adicionalmente, por el Teorema de Pitágoras, tenemos que la hipotenusa de un
triángulo grande (como el conformado por B, C y A) mide
1
1  1 / 2 2  5 / 4    5 , luego, por los argumentos dados anteriormente, las
2
oblicuas determinan segmentos de longitud de dos quintos de esa diagonal (el cateto
mayor de B), dos quintos de esa diagonal (un lado del cuadrado del centro) y un quinto
de la misma (el cateto menor de A), así que el lado del cuadrado interior es
1
 2  1 
, luego su área es 1 / 5 cm 2 .
   5 
5
 5  2 
Solución 16. La cruz tiene dos caras de mayor tamaño y otras caras pequeñas. Estas
caras pequeñas son 3 por cada una de sus cuatro brazos. Entonces tenemos 2 + 4(3) =
14. La respuesta es (b).
Solución 17. De la segunda figura observamos que la mitad de la cantidad total de
líquido equivale a 4 Kg., por lo tanto la cantidad total de líquido equivale a 8 Kg. y así,
el envase vacío pesa 2 Kg. La respuesta es (c).
Solución 18. La expresión A000 + A998 + A999 = 22997 se puede escribir como
A(1000) + A(1000) + 998 + A(1000) + 999 = 22997
A(1000) + A(1000) + A(1000) = 22997 - 1997
A(3000) = 21000
A = 21000/3000
A= 7
La respuesta es (d).
Solución 19. Observemos que la serie se forma de la siguiente manera: el segundo
término es el doble del primero más 1, el tercer término es el doble del segundo menos
1, el cuarto término es el doble del tercero más 1 y así sucesivamente, por lo tanto el
sexto término es el doble del quinto más 1, es decir, (2x21) + 1 = 43. La respuesta es
(b).
Solución 20. Observemos el arreglo siguiente:
Vemos que cumple con las condiciones pedidas, por lo tanto el menor número de
monedas en el cuadriculado es 5. La respuesta es (a).

Solución 21. Las áreas aportadas por los cuadrados son 102  8 2  6 2  200, mientras
1
que el área del triángulo no sombreado es  1010  8  6  120, así que el área
2
2
sombreada mide 80 cm . La respuesta es (c).
Solución 22. La menor diferencia la obtenemos formando con los cinco números el
menor número de tres cifras, y restándole el mayor número de 2 cifras, es decir
134 – 75 = 59. La respuesta es (b).
Solución 23. Fijémonos que en la segunda posición de los cuatriminós se ubican los
números que son múltiplos de 6, y como 2004 es múltiplo de 6, éste se debe de ubicar
en la segunda posición de alguno de los cuatriminós, por lo tanto el 2006 se ubica en la
cuarta posición de un cuatriminó. La respuesta es (d).
Solución 24. Por tener diámetro de 4cm., la longitud del arco bC es igual a la cuarta
parte del perímetro de la tapa, que es 4  , así que el arco bC mide  centímetros.
Ahora, al girar un cuarto de vuelta, avanza  cm., y entonces en la figura 2 AC mide 
cm. y la altura del triángulo ABC es igual al radio de la tapa, que es de 2 centímetros.
1
Por lo tanto el área del triángulo ABC será 2  cm2 .=  cm2. La respuesta es (b).
2
Solución 25. El paralelogramo puede ser cortado en dos triángulos congruentes con los
dos triángulos pequeños, al igual que el triángulo mediano y los cuadrados pequeños,
por lo que en una mitad caben 8 triángulos pequeños, cada uno de los cuales mide
1 2
1 2 1
 cm , así que el paralelogramo mide 2  cm = cm2. La respuesta es (a).
8
 16 
 16 
Solución 26. Vamos a llamar x y z a los números del enunciado. Sabemos que
5
x / z  2 / 5 , es decir, z    x . Si z fuera mayor que x entonces z  x  21 , por lo
2
5
que x  21    x , y resolviendo encontramos x = 14 y por tanto z = 35. Si z fuera
2
menor que x entonces, repitiendo los pasos, nos queda que z  x  21 por lo que
5
x  21    x , y resolviendo encontramos que x = -14 y por tanto z = -35. La
2
respuesta es (a).
Solución 27. PQRS es un cuadrado y la suma del área sombreada que se encuentra
fuera de PQRS es igual al área sin sombrear dentro de PQRS, por tanto el área total
sombreada es igual al área del cuadrado PQRS. Como PB=BQ=AB/2, por el Teorema
de Pitágoras PQ  PB2  BQ2 , así que el lado del cuadrado PQRS es igual a
2 2  2 2  8 . Concluimos entonces que el área total es
(e).
 8  8   8 . La respuesta es
Solución 28. El área del cuadrado grande menos el área del cuadrado chico se puede
dividir en 4 rectángulos como se muestra en la figura:
El área sombreada es la mitad del área de estos cuatro rectángulos, es decir, (259)/2=16/2=8. Por tanto, el área del cuadrado mediano es el área sombreada más el área
del cuadrado chico, esto es 17. La respuesta es (d).
Solución 29. Apliquemos cuatro veces las operaciones alternadas, empezando con
Op.1:
a
b
c
d
Op.1
d
c
b
a
Op.2
c
d
a
b
Op.1
b
a
d
c
Op.2
a
b
c
d
Entonces cada 4 operaciones volvemos a la figura inicial, esto implica que después de
2004 operaciones tendremos:
Op. 2004
a
b
c
d
Op.1
Op. 2005
d
c
b
a
Op.2
c
d
a
b
Op. 2006
Por tanto, la letra correspondiente es la b. La respuesta es (b)
Solución 30. Si distribuimos el recorrido en semanas y días nos será más fácil.
Observemos que 2006 = 7(286) + 4, así que tenemos 286 semanas de lunes a domingo y
nos sobran 4 días. Ahora, el avance de Gary en cada uno de los días de lunes a viernes
es de 2 cm. porque sube 3 cm. pero durante la noche baja 1 cm. Además, como Gary
empezó un jueves, la suma de lo recorrido del jueves al domingo será 2 cm. + 2 cm. + (2) cm. + (-2) cm. = 4 cm. + (-4) cm. = 0 cm. Por lo tanto el recorrido final será igual a lo
que recorra en 286 semanas completas. Podemos ver que en una semana Gary recorre 2
cm. (5) + -2 cm. (2) = 6 cm. El recorrido final será (286) 6 =1716 cm.
La respuesta es (d).