(3 puntos) Para fabricar dos tipos de cables, A y B, que se venderán

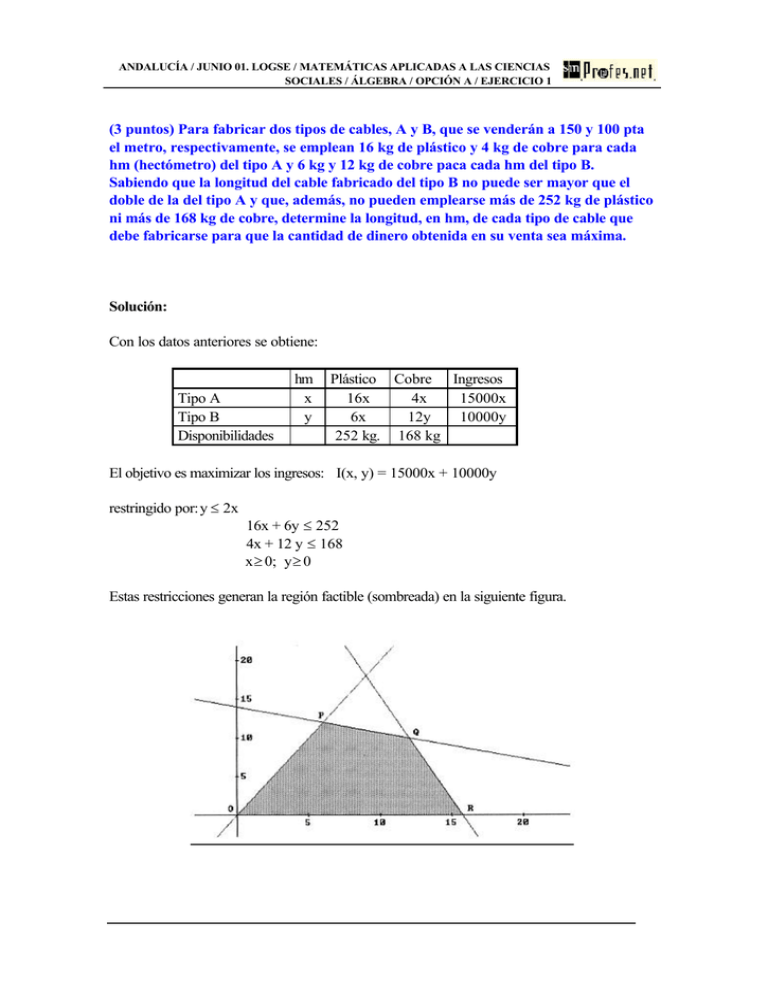
ANDALUCÍA / JUNIO 01. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS
SOCIALES / ÁLGEBRA / OPCIÓN A / EJERCICIO 1
(3 puntos) Para fabricar dos tipos de cables, A y B, que se venderán a 150 y 100 pta
el metro, respectivamente, se emplean 16 kg de plástico y 4 kg de cobre para cada
hm (hectómetro) del tipo A y 6 kg y 12 kg de cobre paca cada hm del tipo B.
Sabiendo que la longitud del cable fabricado del tipo B no puede ser mayor que el
doble de la del tipo A y que, además, no pueden emplearse más de 252 kg de plástico
ni más de 168 kg de cobre, determine la longitud, en hm, de cada tipo de cable que
debe fabricarse para que la cantidad de dinero obtenida en su venta sea máxima.
Solución:
Con los datos anteriores se obtiene:
Tipo A
Tipo B
Disponibilidades
hm
x
y
Plástico Cobre Ingresos
16x
4x
15000x
6x
12y
10000y
252 kg. 168 kg
El objetivo es maximizar los ingresos: I(x, y) = 15000x + 10000y
restringido por:y ≤ 2x
16x + 6y ≤ 252
4x + 12 y ≤ 168
x≥ 0; y≥ 0
Estas restricciones generan la región factible (sombreada) en la siguiente figura.
ANDALUCÍA / JUNIO 01. LOGSE / MATEMÁTICAS APLICADAS A LAS CIENCIAS
SOCIALES / ÁLGEBRA / OPCIÓN A / EJERCICIO 1
Los vértices son:
y = 2x

O = (0, 0), P: 
⇒ P = (6, 12)
4 x + 12 y = 168
16 x + 6 y = 252
Q: 
⇒ Q = (12, 10) y R = (15,75, 0).
 4 x + 12 y = 168
Los ingresos para esos niveles de producción son:
En O,
En P,
En Q,
En R,
I(0, 0) = 0.
I(6, 12) = 210.000 pta
I(12, 10) = 280.000 pta
I(15,75, 0) = 236.250 pta
Los ingresos máximos se obtienen fabricando 12 hm de cable de tipo A y 10 hm del tipo B.