Soluciones

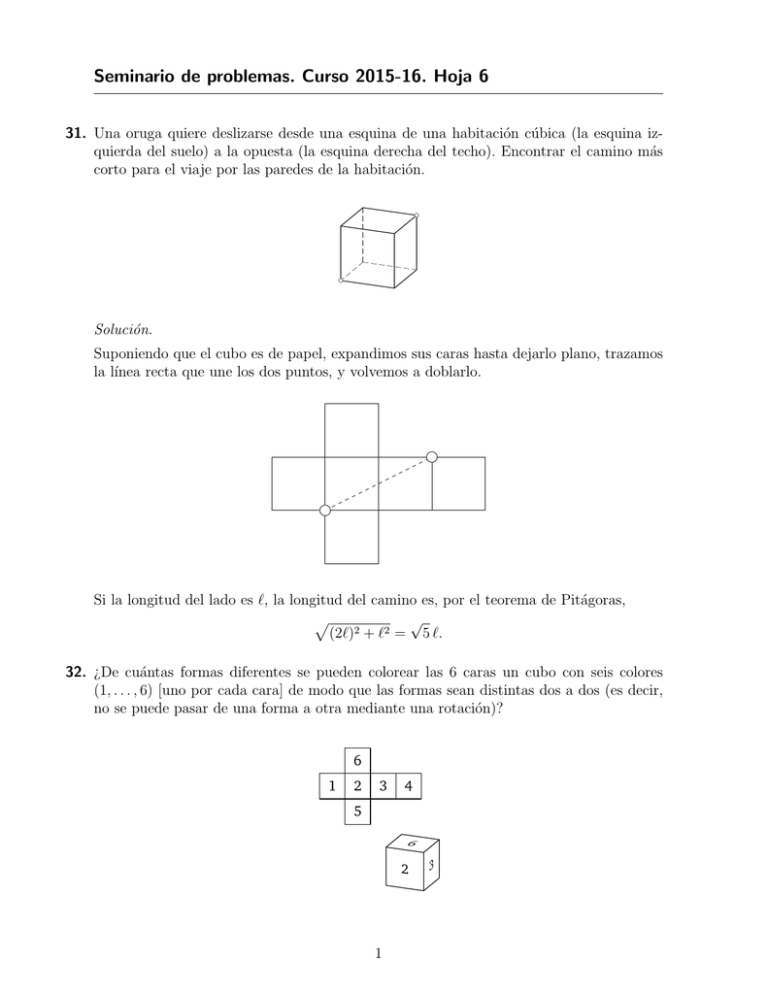
Seminario de problemas. Curso 2015-16. Hoja 6
31. Una oruga quiere
deslizarse
desdeEFTMJ[BSTF
una esquina
habitación
cúbica (la esquina iz 6OB
PSVHB RVJFSF
EFTEFde
VOBuna
FTRVJOB
EF VOB IBCJUBDJ³O
quierda del suelo)
opuesta
(la esquina
derecha
del techo).
Encontrar
el camino más
DºCJDB aMBlaFTRVJOB
J[RVJFSEB
EFM TVFMP
B MB PQVFTUB
MB FTRVJOB
EFSFDIB
corto para elEFM
viaje
por
las
paredes
de
la
habitación.
UFDIP
&ODPOUSBS FM DBNJOP N¡T DPSUP QBSB FM WJBKF QPS MBT QBSFEFT
EF MB IBCJUBDJ³O
Solución.
4F UJFOFO EPT WBTPT EF WPMºNFOFT MJUSPT Z MJUSPT .FEJS VO
MJUSP PCUFOFSMP FO VOP EF MPT WBTPT
Suponiendo que el cubo es de papel, expandimos sus caras hasta dejarlo plano, trazamos
la lı́nea recta que une los dos puntos, y volvemos a doblarlo.
�
�
&O VOB GBNJMJB IBZ DJODP DBCF[BT Z DBUPSDF QJFSOBT $V¡OUBT
QFSTPOBT Z DV¡OUPT QFSSPT GPSNBO MB GBNJMJB
&O DBEB VOP EF MPT MBEPT AB BC Z CA EFM USJ¡OHVMP ABC TF
DPOTUSVZF IBDJB GVFSB VO USJ¡OHVMP FRVJM¡UFSP 1SPCBS RVF TVT DFOUSPT
∗
GPSNBO VO USJ¡OHVMP FRVJM¡UFSP
$V¡OUBT TJNFUS­BT UJFOF UFUSBFESP $V¡OUBT UJFOF VO DVCP
B VO EPEFDBFESP -B TJNFUS­B FT
: VO PDUBFESP : VO JDPTBFESP :
⇤
VOB USBOTGPSNBDJ³O RVF DPOTFSWB MBT EJTUBODJBT
&OUSF MBT TJNFUS­BT
⇤
Si la longitud
del lado
es `, la IBZ
longitud
del camino
es, por SFࢹFYJPOFT
el teorema de
DV¡OUBT
SPUBDJPOFT
Z FOUSF
©TUBT DV¡OUBT
FOPitágoras,
DBEB
VOP EF MPT DJODP DBTPT QSPQVFTUPT
pA
C√
2
(2`)2 +
⇤ ` = 5 `.
formas
%F DV¡OUBT
GPSNBT
EJGFSFOUFT
TF QVFEFO
MBTcubo
DBSBT
32. ¿De cuántas
diferentes
se pueden
colorear
las 6DPMPSFBS
caras un
conVOseis colores
DVCP DPO TFJT DPMPSFT (1, . . . , 6) <VOP QPS DBEB DBSB> EF NPEP RVF MBT
(1, . . . , 6) [uno por cada cara] de modo que las formas sean distintas dos a dos (es decir,
GPSNBT TFBO EJTUJOUBT EPT B EPT FT EFDJS OP TF QVFEF QBTBS EF VOB
no se puede pasar de una forma a otra mediante una rotación)?
GPSNB B PUSB NFEJBOUF VOB SPUBDJ³O
�
�
�
�
�
�
�
�
�
%F DV¡OUBT GPSNBT EJTUJOUBT TF QVFEFO QFSNVUBS n PCKFUPT
)BZ TFJT QFSNVUBDJPOFT QPTJCMFT QBSB
1 n = 3 (1, 2, 3) (1, 3, 2) (2, 1, 3)
(2, 3, 1) (3, 1, 2) (3, 2, 1) $V¡OUBT IBZ QBSB n = 4 n = 5 n = 6
n = 10
Solución.
Pintamos una cara de abajo un color.
Para pintar la cara de arriba disponemos de cinco colores posibles.
Para pintar las caras laterales disponemos de cuatro colores, pero se trata de permutaciones circulares (con la cara de arriba y abajo fija, podemos girar las cuatro caras
laterales).
Por tanto, habrá un total de 5 · 4!/4 = 5 · 3! = 30 formas distintas de colorear el cubo.
33. Se eligen 4 vértices de un paralelogramo entre los nodos de una cuadrı́cula. Si ningún
nodo de la cuadrı́cula queda encerrado en el interior del paralelogramo, probar que el área
del paralelogramo es igual a la de cada uno de los cuadros de la cuadrı́cula.
a = 2, b = 2
$PO de
MBTlaDPOEJDJPOFT
EF MB QSFHVOUB
TJestán
a OPEPT
FTU¡O FODFSSB
34. Con las condiciones
pregunta anterior,
si a nodos
encerrados
en el interior del
EPT FO
JOUFSJPS
EFMen
QBSBMFMPHSBNP
Z b OPEPT
FTU¡Odel
FOparalelogramo.
MB GSPOUFSB
paralelogramo
y bFMnodos
están
la frontera, calcular
el área
$BMDVMBS FM ¡SFB EFM QBSBMFMPHSBNP
Solución conjunta.
Ambos casos
casos
particulares del
teorema
de Pick, TJHVF
que dice
lo siguiente:
son1BSB
QBSBMFMFQ­QFEPT
FO USFT
EJNFOTJPOFT
TJFOEP
DJFSUB MB
BࢸSNBDJ³O
EF cuyos
MB QSFHVOUB
tienen coordenadas enteras. Si a es el número de
Sea un polı́gono
simple
vértices
puntos de coordenadas enteras en el interior del polı́gono, y b es el número de puntos de
coordenadas
en el borde,
área
del polı́gono
es MB TVDFTJ³O
enteras
-PT OºNFSPT
EFM entonces
DPOFKP Pel EF
'JCPOBDDJ
GPSNBO
1, 1, 2, 3, 5, 8, 13, 21, 34, . . . FO MB RVF an+2 = an+1 + an QBSB DBEB
b
n = 1, 2, . . . an FT FM FO©TJNP
U©SNJOP
EF1.MB TVDFTJ³O
&ODPOUSBS FM
Área =
a+ −
N¡YJNP DPNºO EJWJTPS EF MPT OºNFSPT2a100 Z a99 &ODPOUSBS
OºNFSP
EF $BUBMBO
EFdesapercibido
GPSNBT EF EJWJEJS
n (Pick era
Lo probó Georg
AlexanderFMPick
en 1899,
pero pasó
hastaVO1969
¡HPOP
QPS nazi).
MBT EJBHPOBMFT RVF OP TF
judı́o y murió
en DPOWFYP
1942 en FO
un USJ¡OHVMPT
campo de DPSU¡OEPMP
concentración
JOUFSTFRVFO 1PS FKFNQMP c(4) = 2 c(5) = 5 c(6) = 14 $V¡OUPT TF
Ejemplo:
QVFEFO FODPOUSBS QBSB c(10)
2
&O VO UPSOFP QBSUJDJQBO n FRVJQPT MPT RVF QJFSEFO BCBOEPOBO MB
Puntos del interior = 5
Puntos de la frontera = 16
Área = 5 +
16
− 1 = 12
2
4
− 1 = 1. (Además, en el ejemplo del dibujo se ve que
2
podemos ((juntar trocitos)) para recomponer un cuadrado.)
b
En el problema 34, Área = a + − 1.
2
Esquema de la demostración del Teorema de Pick.
En el problema 33, Área = 0 +
Primero tenemos que poner un poco de notación.
Llamamos P al polı́gono simple cuyos vértices tienen coordenadas enteras. Entonces, dado
un punto A de coordenadas enteras, decimos que la contribución de A a P es


si A está en el interior de P ,
1,
cP (A) = 1/2, si A está en la frontera de P ,


0,
si A está en el exterior de P .
Con esta notación, el teorema de Pick afirma que
X
Área(P ) =
cP (A) − 1
A
donde el sumatorio se hace sobre todos los puntos A de coordenadas enteras (obviamente,
de los puntos exteriores podemos prescindir pues no aportan nada a la suma).
Ahora el teorema se demuestra en pasos:
(a) Rectángulos
Puntos del interior = (b − 1)(h − 1)
h
Puntos de la frontera = 2(b − 1) + 2(h − 1) + 4 = 2(b + h)
Área = bh = (b − 1)(h − 1) + 21 · 2(b + h) − 1
b
(b) Trapecios con tres lados paralelos a los ejes:
3
b2
C
Área(T ) =
T0
T
h
¿
X
D
b1
b1 + b2
·h
2
cT (A) =
A
b 1 + b2
·h
2
?
T 0 es el trapecio simétrico de T , y llamamos R al rectángulo que forman.
Es fácil ver que:
• cT (A) + cT 0 (A) = cR (A) para cualquier punto A excepto para C y D.
X
X
•
cT (A) =
cT 0 (A) (por simetrı́a).
A
A
Entonces
1 + (b1 + b2 )h
paso (a)
=
X
A
X
=1+
X
cT (A) +
cT 0 (A)
A6=C,D
= −1 + cT (C) + cT (D) + cT 0 (C) + cT 0 (D) +
= −1 + 2
cR (A)
A6=C,D
A6=C,D
X
X
cR (A) = cR (C) + cR (D) +
X
A6=C,D
cT (A).
A
Despejando,
X
A
cT (A) − 1 =
tal como buscábamos.
(c) Triángulos:
(d) Cuadriláteros:
4
b1 + b2
· h,
2
cT (A) +
X
A6=C,D
cT 0 (A)
(e) Polı́gonos de n lados: inducción sobre n.
35. Los números de Fibonacci forman la sucesión 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . , en la que an+2 =
an+1 + an para cada n = 1, 2, . . . (an es el n-ésimo término de la sucesión). Encontrar el
máximo común divisor de los números a100 y a99 .
Solución.
Supongamos que tenemos una división de enteros (los suponemos no negativos, salvo el
resto que puede ser 0)
D =d·c+r
Si r = 0, d divide a D, luego mcd(D, d) = d. En otro caso, ¿cómo calcular mcd(D, d)?
(a) Si un número n divide a D y a d, entonces D = nD1 y d = nd1 , con lo cual nD1 =
nd1 c + r, es decir
r = n(D1 − d1 c),
y por tanto n divide a d (ya lo sabı́amos) y a r.
(b) Si un número n divide a d y a r, entonces d = nd1 y r = nr1 , con lo cual D = nd1 c+nr1 ,
es decir
D = n(d1 c − r1 ),
y por tanto n divide a d (ya lo sabı́amos) y a D.
Las dos cosas (a) y (b) ocurren para cualquier divisor n, y por tanto el mayor divisor será
el mismo. Es decir,
mcd(D, d) = mcd(d, r).
Lo que ocurre al hacer esto es que, sin más que hacer una división, hemos cambiado D
por r, ¡un número mucho más pequeño!, luego es más fácil calcular el mcd.
Si hacemos esto reiteradamente (es decir, si empleamos el mismo truco para calcular
mcd(d, r), etc.), esto es lo que se denomina algoritmo de Euclides para calcular en máximo
común divisor (si los números de partida D y d no son muy sencillos, es mucho más rápido
que el clásico ((descomponer D y d en factores y tomar los factores comunes con el menor
exponente))).
En el caso de los números de Fibonacchi, tenemos
an+2 = an+1 · 1 + an
luego mcd(an+2 , an+1 ) = mcd(an+1 , an ). Reiterando,
mcd(an+2 , an+1 ) = mcd(an+1 , an ) = mcd(an , an−1 ) = · · ·
= mcd(a4 , a3 ) = mcd(a3 , a2 ) = mcd(2, 1) = 1.
De hecho, ¡con los números de Fibonacci es como más lento discurre el algoritmo de
Euclides para la calcular el mcd!
36. Encontrar el número (de Catalan) de formas de dividir un n-ágono convexo en triángulos
cortándolo por las diagonales que no se intersequen. Por ejemplo, c(4) = 2, c(5) = 5,
c(6) = 14. ¿Cuántas formas se pueden encontrar para c(10)?
5
¡HPOP DPOWFYP FO USJ¡OHVMPT DPSU¡OEPMP QPS MBT EJBHPOBMFT RVF OP TF
JOUFSTFRVFO 1PS FKFNQMP c(4) = 2 c(5) = 5 c(6) = 14 $V¡OUPT TF
QVFEFO FODPOUSBS QBSB c(10)
Solución.
&O VO UPSOFP QBSUJDJQBO n FRVJQPT MPT RVF QJFSEFO BCBOEPOBO MB
DPNQFUJDJ³O Z FM HBOBEPS TF EFDJEF USBT n − 1 FODVFOUSPT &M DVBESP
Es un problema muy conocido; fue propuesto por Euler a Goldbach en 1751.
EFM UPSOFP TF QVFEF FTDSJCJS EF GPSNB TJNC³MJDB DPNP QPS FKFNQMP
Para un polı́gono de 6 lados, las 14 posibilidades son estas:
Cn
=
Cn−1 C0 + Cn−2 C1 + · · · + C1 Cn−2 + C0 Cn−1
(5)
Beginning in the next section, we will be able to use these recursive formulas to show that the
counts of other configurations (triangulations of polygons, rooted binary trees, rooted tress, et cetera)
satisfy the same formulas and thus must generate the same sequence of numbers.
But simply by using the formulas above and a bit of arithmetic, it is easy to obtain the first
few Catalan numbers: 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900,
2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020,
91482563640,
343059613650,
1289904147324,
. n genérico, vamos a ver cómo podemos
Para ver cuántas
configuraciones
hay para. .un
razonar en un polı́gono de 8 lados (esto serı́a un paso de inducción, ¡pero para hacer
es más Polygon
sencillo concretar
algo!). Ası́ pues, partamos de un octógono, reiterando
2.1dibujos
Counting
Triangulations
que los mismos argumentos se aplicarı́an a cualquier polı́gono convexo.
It isEn
notelhard
to see that
the polygoneltriangulations
discussed
in section
1.4los
cantriángulos
be countedque
in much
octógono,
consideremos
lado superior,
y dibujemos
todos
se
the forman
same way
as
the
balanced
parentheses.
See
Figure
6.
usando ese lado. Son estos 6:
A derecha e izquierda de ese
triángulo
hay sendos
polı́gonos (((vacı́os)) en el primer y
Figure
6: Octagon
Triangulations
último dibujo).
In the
figure we
consider
thepolı́gono
octagon, de
but7itlados
should
clear that the
sameaargument
applies
En
el primer
caso,
hay un
a be
la izquierda
y nada
la derecha;
eso to
anyse
convex
Consider
the horizontal
lineelatsegundo
the top of
theunpolygon.
puedepolygon.
descomponer
de c(7)
formas. En
hay
polı́gonoAfter
de 6triangulation,
lados a la it
willizquierda
be part ofyexactly
one
triangle,
and
in
this
case,
there
are
exactly
six
possible
triangles
of which
uno de 3 a la derecha; la triangulación del octógono se puede completar
de
it can be a part. In each case, once that triangle is selected, there is a polygon (possibly empty) on
the right and the left of the original triangle that must
6 itself be triangulated.
What we would like to show is that a convex polygon with n > 3 sides can be triangulated in
C
ways. Thus the octagon should have C
= C triangulations.
c(6) · c(3) formas. En el tercero, un polı́gono de 5 lados a la izquierda y uno de 4 a la
derecha; la triangulación se completa de c(5) · c(4) formas. Etcétera. Ası́ pues, el número
de descomposiciones del octógono es
c(8) = c(7) + c(6) · c(3) + c(5) · c(4) + c(4) · c(5) + c(3) · c(6) + c(7).
Si denotamos c(2) = 1, esto ese puede escribir ası́:
c(8) = c(7) · c(2) + c(6) · c(3) + c(5) · c(4) + c(4) · c(5) + c(3) · c(6) + c(2) · c(7).
En general,
c(n + 1) =
n
X
k=2
c(n + 2 − k)c(k),
que sirve una fórmula recurrente de ir obteniendo todos los c(n).
Con esto, partiendo de c(2) = 1 (por convención) y c(3) = 1, vamos obteniendo
c(4) = 2, c(5) = 5, c(6) = 14, c(7) = 42, c(8) = 132,
c(9) = 429, c(10) = 1430, c(11) = 4862, c(12) = 16796.
A menudo se utiliza Cn para denotar c(n + 2) (ası́ C1 se refiere al polı́gono de 3 lados, el
primero que tiene sentido, Cn al polı́gono de n + 2 lados, y C0 = c(2) = 1 por convención).
Con esta notación, para el polı́gono de 8 lados tenemos
C6 = C5 · C0 + C4 · C1 + C3 · C2 + C2 · C3 + C1 · C4 + C0 · C5
y, en general,
Cn+1 =
n
X
Cn Cn−k ,
C0 = C1 = 1.
(∗)
k=0
Esa es la relación de recurrencia de los denominados números de Catalan. Hay muchos
problemas combinatorios que generan esa sucesión de números. También cumplen
2n
1
,
(∗∗)
Cn =
n+1 n
que es como se escriben normalmente con una ((fórmula cerrada)) (no es muy sencillo transformar (∗) en (∗∗)). En la The On-Line Encyclopedia of Integer Sequences, los números
de Catalan está en https://oeis.org/A000108
7