1 Formas argumentales válidas Mencionamos anteriormente que un

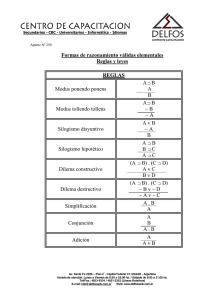
Formas argumentales válidas
Mencionamos anteriormente que un argumento deductivo válido será aquel que no puede tener
una conclusión falsa si sus premisas son verdaderas. Dicho de otro modo, bajo el supuesto de que
son verdaderas las premisas de un argumento deductivo válido, la conclusión necesariamente
también lo será.
Con el fin de distinguir entre argumentos válidos e inválidos analizaremos algunas formas
argumentales válidas que son demasiado comunes y que pueden comprenderse intuitivamente.
Debemos ser capaces de identificarlas dondequiera que aparezcan.
1. Silogismo disyuntivo.
Una de las formas argumentales válidas más simples depende del hecho de que en toda
disyunción verdadera al menos uno de los elementos tiene que ser verdadero. Por lo tanto, si uno
de los elementos es falso, el otro tiene que ser verdadero. Los argumentos con esta forma son
muy comunes. Vemos un ejemplo. "Todo círculo es una curva o una recta; es una curva; luego, no
es una recta". Y si decimos: “O estudias lógica con empeño o te creerás las falacias de los políticos.
Te crees las falacias de los políticos” ¿Cuál será la conclusión?
La forma general de simbolizar el silogismo disyuntivo es la siguiente:
AvB
¬B
.·. A
AvB
A
.·. ¬B
AvB
¬A
.·. B
AvB
B
.·. ¬A
Donde A y B son dos enunciados simples o compuestos, v es una disyunción, ¬ es una negación y
.·. es un indicador de conclusión.
El siguiente argumento también tiene la forma de silogismo disyuntivo: “Es de día y hay sol a
menos que sea de noche y esté oscuro. No es el caso que sea de día y haya sol. En consecuencia,
es de noche y está oscuro.” Su simbolización sería de este modo
(p • q) v (r • s)
¬ (p• q)
.·. (r • s)
Notemos que aunque el argumento está conformado por enunciados compuestos sigue
conservando una forma de silogismo disyuntivo. Esto es porque, si comparamos la simbolización
del argumento con la forma del silogismo disyuntivo, entonces A = (p• q) y B = (r • s).
2. Modus Ponens
El tipo más simple de argumento intuitivamente válido que involucra enunciados condicionales se
ejemplifica en el siguiente argumento. “Si el segundo habitante dijo la verdad entonces sólo un
habitante es político. El segundo habitante dijo la verdad. Por lo tanto, sólo un habitante es
político”.
La forma de este argumento se conoce como modus ponens, que significa el método de afirmar.
Esta forma general es la siguiente:
1
A→B
A
.·. B
Donde A y B, como habíamos mencionado, son dos enunciados simples o compuestos, → es un
símbolo de condicional y .·. es un indicador de conclusión. Insistamos en que las letras A y B no
representan necesariamente enunciados simples, sino que también pueden ser compuestos.
3. Modus tollens
Esta forma argumental normalmente es utilizada para determinar la falsedad de algún enunciado
puesto en duda. A manera de ejemplo, analicemos el siguiente argumento.
“Si ayer fuiste al médico, tienes que tener una receta médica. No tienes una receta médica. Por
consiguiente, no fuiste ayer al médico”. Lo que se pone en duda es que la persona haya ido un día
antes al médico y se demuestra que tal situación es falsa con la inexistencia de una receta médica.
En general el Modus tollens, que significa el método de negar, se simboliza así.
A→B
¬B
.·. ¬A
Donde, como ya hemos dicho, A y B son dos enunciados simples o compuestos, → es un símbolo
de condicional, ¬ lo es de negación y .·., de conclusión.
4. Silogismo hipotético
Otro tipo común de argumento intuitivamente válido contiene sólo enunciados condicionales. He
aquí un ejemplo: “Si está nublado, probablemente va a llover. Si probablemente va a llover
entonces necesito un paraguas. Así que, si está nublado, necesitaré un paraguas” La forma general
de este argumento es:
A→B
B→C
.·. A → C
Donde, A, B y C son tres enunciados simples o compuestos, → es un símbolo de condicional y .·.,
de conclusión.
2