Grafos con independencia promedio arbitraria

PROYECTO FIN DE CARRERA
Independencia promedio de grafos y
polinomio de Jones. Aplicaciones en
ingeniería
Autora: Nadia Srour Calvo
Departamento proponente: Matemática Aplicada
Tutor: Pedro M. González Manchón
Febrero 2007
Autora:
Nadia Srour Calvo
VºBº del tutor:
Pedro M. González Manchón
En el nombre de Dios, el clemente, el misericordioso...
Me gustaría dar las gracias a todos aquellos que han permanecido
a mi lado durante la realización de este proyecto, apoyándome y
ayudándome de manera diferente, pero igualmente útil. Estos
agradecimientos van dirigidos a mi familia y amigos, muy en
particular a mis padres y a mis dos hermanos.
También quiero agradecer de manera muy especial a mi tutor,
Pedro María González Manchón, por brindarme la posibilidad de
realizar este proyecto e involucrarse en la elaboración del mismo
casi tanto como yo.
INTRODUCCIÓN ............................................................................................................ 1
1. ISOMERÍA TOPOLÓGICA ........................................................................................ 5
Grafos, nudos y enlaces ................................................................................................ 5
Grafo de una molécula .................................................................................................. 5
Grafos topológicamente complejos .............................................................................. 6
Simetría especular de las moléculas ............................................................................. 8
Reconocimiento de la simetría vía el polinomio de Jones ........................................... 9
Coeficiente extremo del polinomio de Jones y teoría de grafos ................................. 11
2. TEORÍA DE GRAFOS .............................................................................................. 15
Grafos convertibles ..................................................................................................... 16
Sobre grafos no planos y el teorema de Kuratowski .................................................. 18
3. INDEPENDENCIA PROMEDIO DE GRAFOS ....................................................... 21
Definición de I(G) ...................................................................................................... 21
Leyes para el cálculo de I(G) ...................................................................................... 22
4. GRAFOS CON INDEPENDENCIA PROMEDIO ARBITRARIA .......................... 25
Nuestra mejora de la solución ................................................................................... 27
Comparativa de las soluciones ................................................................................... 29
5. ANALIZANDO CUÁNDO UN GRAFO ES CONVERTIBLE ................................ 33
Ciclos puros ................................................................................................................ 33
Índices de conexión de dos ciclos............................................................................... 34
6. GRAFOS CON POCOS VÉRTICES. PROGRAMACIÓN ...................................... 41
Independencia promedio tres ...................................................................................... 42
Grafos con siete vértices ......................................................................................... 42
Grafos con ocho vértices ........................................................................................ 42
Grafos con nueve vértices....................................................................................... 44
Grafos con diez vértices ......................................................................................... 46
Grafos con once vértices......................................................................................... 56
Programación con MATLAB ..................................................................................... 66
Enumeración de matrices e independencia promedio ............................................ 68
7. CONCLUSIÓN .......................................................................................................... 71
BIBLIOGRAFÍA ............................................................................................................ 73
INTRODUCCIÓN
Observemos la molécula
o
o
o
o
o
o
o
N
N
N
N
N
N
N
N
o
o
o
o
o
o
o
Figura 1. Una molécula con forma de nudo trébol...
y su imagen especular
o
o
o
N
N
N
N
N
N
N
N
Figura 2. ... y su imagen especular
Estas moléculas, sintetizadas por Dietrich–Buchecker y Sauvage [DS] en 1989, son
los primeros ejemplos de moléculas con la forma de un nudo. Físicamente, un nudo se
obtiene “anudando” un cordón de zapatos y uniendo después sus extremos. Las
moléculas anteriores pueden ser representadas de modo sintético mediante los llamados
nudos trébol (de mano derecha y de mano izquierda):
Figura 3. Los nudos trébol de mano derecha y mano izquierda
Obsérvese que la imagen especular K* de un nudo K se obtiene invirtiendo todos los
cruces del nudo K.
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Desde un punto de vista experimental, el determinar que estas moléculas son
distintas se basa en la observación de sus propiedades físico-químicas, como pueden ser
propiedades ópticas (experimento de Pasteur), el sabor (limonada o naranjada), etc.
La teoría de nudos, y en concreto el polinomio de Jones, provee una herramienta
matemática que puede probar de modo directo que ambas moléculas son distintas, es
decir, no podemos superponerlas sin romperlas, por muy flexibles que las imaginemos.
Para poder distinguir dos nudos entre si, Vaughan Jones descubrió, en la década de
los ochenta, una manera unívoca de asociar a cada nudo un polinomio, de manera que si
dos nudos son equivalentes, entonces los polinomios asociados coinciden. Así que este
polinomio, llamado desde entonces polinomio de Jones, es una herramienta para
distinguir nudos no equivalentes. La trascendencia matemática de este descubrimiento y
sus múltiples implicaciones en otras ramas de las matemáticas y la física le valieron a
Jones, en 1990, la medalla Field, equivalente a los premios Nobel en matemáticas.
Los polinomios de Jones VK(t) de un nudo K y VK*(t) de su imagen especular K*
son simétricos respecto al intercambio de la variable t con t–1. Por ejemplo, VK(t) = t + t3
– t4 mientras que VK*(t) = t–1 + t–3 – t–4 para los nudos de la figura 3. Como ambos
polinomios son distintos, se deduce que ambos nudos son no equivalentes, es decir, no
puede deformarse uno para obtener el otro.
En particular, para que hubiese simetría especular en el nudo, su polinomio de Jones
debería ser simétrico respecto al intercambio de t con t–1. Supongamos entonces que
VK(t) =amtm +...+ aMtM es el polinomio de Jones de cierto nudo K. Si sus coeficientes
extremos son distintos, esto es, si am ≠ aM, entonces este polinomio no es simétrico
respecto al intercambio de t con t–1, y por tanto K no experimenta simetría especular, es
decir, K ≠ K*.
Este proyecto se centra en el estudio de los coeficientes extremos am y aM, basado en
el concepto de independencia promedio de un grafo. Partiendo de un nudo K y mediante
un proceso mecánico, construiremos un grafo GK (un grafo es un conjunto de vértices y
aristas uniendo pares de vértices). Estos grafos GK serán llamados convertibles, por
obtenerse a partir de un nudo K mediante el proceso de suavización por A-cuerdas. Este
proceso se ilustra en la siguiente figura para un ejemplo concreto de enlace (colección
disjunta de nudos):
Figura 4. Obtención del grafo a partir de un enlace
El primer paso de este proceso consiste en cambiar cada cruce del nudo o enlace por
una A-cuerda (en azul) mediante un proceso llamado suavización. Los extremos de
estas A-cuerdas descansan en las llamadas circunferencias de referencia, pintadas en
negrita. El segundo paso convierte cada A-cuerda con extremos en una misma
circunferencia de referencia en un vértice del grafo. Si los extremos de dos cuerdas
alternan en la misma circunferencia de referencia, entonces uniremos por una arista los
vértices correspondientes, y al revés, si sus extremos no alternan, no habrá una arista
2
Introducción
que una dichos vértices. Al precisar después esta construcción, se deducirá que el
número de vértices del grafo obtenido es menor o igual al número de cruces en el nudo
o enlace original.
Un concepto asociado a GK es el de independencia promedio. Se trata de un número
entero I(GK) que se obtiene en términos de conjuntos independientes de vértices. Un
subconjunto de vértices de un grafo se dice independiente si no contiene dos vértices
adyacentes. A cada subconjunto de vértices independiente le asociamos el valor 1 si su
cardinal es par, –1 si su cardinal es impar. La independencia promedio I(G) del grafo G
se obtiene sumando todos estos valores ±1, al considerar toda la familia de subconjuntos
de vértices independientes del grafo G.
Un teorema de Bae y Morton [BM] asegura que el coeficiente extremo aM del
polinomio de Jones VK(t) del nudo K coincide, quizás salvo signo, con la independencia
promedio I(GK). Igualmente, am coincide, quizás salvo signo, con la independencia
promedio I(GK*). Así que, si los valores absolutos de estas dos independencias
promedio son distintos, podemos asegurar que el nudo K no experimenta simetría
especular, es decir, es distinto del nudo K*.
Como ya hemos dicho antes, a partir del nudo K la construcción del grafo
convertible asociado GK es mecánica. El cálculo de la independencia promedio I(GK)
también lo es. De esta manera se tiene un proceso algorítmico que podría descartar que
el nudo K tenga simetría especular.
La explicación detallada de estas ideas se expone con mayor profundidad y
detenimiento en el primer capítulo de este proyecto. El grueso del trabajo, capítulos dos
a siete, está dedicado a aspectos puramente matemáticos, relacionados con el concepto
de independencia promedio de grafos.
En el artículo [BM], Bae y Morton plantearon la cuestión de si, dado un número
natural arbitrario n, existe un grafo G convertible cuya independencia promedio sea n.
Esto fue respondido positivamente en el artículo [M]. En este proyecto se investigan los
posibles grafos soluciones con el menor número de vértices posible. A este respecto,
nuestra aportación puede resumirse en los siguientes puntos:
1. Hemos demostrado que para independencias promedio 2 y 3 la solución
aportada en [M] es la óptima, es decir, la de menor número de vértices.
2. Para cada entero mayor que tres, aportamos una solución que simplifica la
dada en [M], consiguiendo una disminución de vértices significativa. El
grafo construido utiliza como pieza básica el hexágono, al igual que en [M].
3. Hemos creado, utilizando MATLAB, programas que permiten el cálculo de
la independencia promedio de grafos y la búsqueda de grafos con
independencia promedio dada, operaciones irrealizables a mano. Estos
programas facilitaron la demostración del punto 1 citado más arriba.
Dado que el reconocer a simple vista si un grafo es o no convertible es una tarea
difícil, en el presente trabajo hemos abordado también la cuestión de la caracterización
de los grafos convertibles, aportando varias pautas que facilitan su reconocimiento.
3
1. ISOMERÍA TOPOLÓGICA
El propósito de esta sección es detallar las implicaciones en isomería química de nuestro
trabajo. Algunos conceptos matemáticos de esta sección son sólo presentados de un
modo intuitivo.
Grafos, nudos y enlaces
Podemos hacernos una primera idea de lo que es un grafo definiéndolo como una
colección de vértices y aristas disjuntas que conectan pares de vértices. En este trabajo
no consideraremos grafos que tengan dos vértices unidos por más de una arista, ni
aristas cuyos extremos sean un mismo vértice (bucles).
Figura 5. Tipos de aristas no permitidas
Físicamente, un nudo puede imaginarse como el resultado de “anudar” un cordón de
zapatos y después unir los extremos de éste. Desde un punto de vista matemático, un
nudo es un círculo sumergido en el espacio que no se puede deformar de manera que
descanse en el plano. En la siguiente figura mostramos el nudo trébol, el más sencillo de
todos los nudos no triviales:
Figura 6. Un nudo trébol
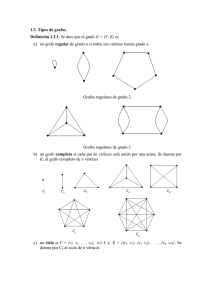
Si en un nudo marcamos tres o más vértices, se obtiene un tipo sencillo de grafo,
llamado ciclo. Recíprocamente, si en un grafo de tipo ciclo eliminamos todos sus
vértices, obtendremos un nudo.
Por último, definimos un enlace como una colección finita y disjunta de nudos.
Grafo de una molécula
El grafo de una molécula (molecular bound graph en inglés) es un modelo de ésta, en
donde los vértices del grafo representan átomos o una colección de átomos y las aristas
representan enlaces químicos o cadenas de átomos.
En ocasiones los vértices o las aristas del grafo están etiquetados. Por ejemplo,
resulta interesante etiquetar los vértices si éstos se corresponden con átomos de
diferentes elementos químicos, o en el caso de las aristas para poder distinguir entre
enlaces simples y dobles, o incluso triples.
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Átomo
Vértice
Colección de átomos
Grafo
molecular
Enlace (simple, doble, triple)
Arista
Cadena de átomos
Grafos topológicamente complejos
La estereoquímica es el estudio de la estructura tridimensional de las moléculas y la
topología es el estudio de aquellas propiedades de los objetos geométricos que son
invariantes bajo transformaciones continuas.
La molécula típica no es plana, pero si pensamos que el grafo molecular que lo
representa es de goma, totalmente flexible, podemos deformarlo de manera que acabe
descansando en el plano. Cuando esto no es posible decimos que el grafo molecular es
topológicamente complejo. Fue necesario esperar hasta 1961 para conocer la primera
molécula topológicamente compleja.
Ya en el año 1910 los químicos intentaban sintetizar una molécula que estuviese
constituida por un par de anillos enlazados. Sin embargo, no fue hasta el año 1961
cuando Frisch y Wasserman lo lograron [FW], con una molécula formada por dos
anillos de hidrocarburos de 34 átomos cada uno. La forma de esta molécula se recoge en
la siguiente figura, en donde hemos suprimido los vértices que representan a los
distintos átomos:
Figura 7. El enlace de Hopf
En teoría de nudos este enlace se conoce con el nombre de enlace de Hopf. Es fácil
imaginar que dicho enlace no puede ser deformado en una figura plana por muy flexible
que sea, así que la molécula representada es topológicamente compleja.
Frisch y Wasserman trabajaron también, aunque sin éxito, en la síntesis de
moléculas con forma de nudo.
En el año 1981, los laboratorios de Simmons y Maggio [SM] y de Paquette y
Vazzeux [PV] sintetizaron, de manera independiente, otra molécula topológicamente
compleja, conocida con el nombre de molécula de Simmons–Paquette.
Si se observa su grafo molecular (ver siguiente figura), en la unión de aristas se
encontrarían los átomos de carbono, los átomos de oxígeno vienen representados
mediante la letra O y los átomos de hidrógeno se omiten con objeto de lograr una mayor
6
Isomería topológica
simplicidad, como se hará en lo sucesivo. Ya que este grafo contiene un grafo completo
K5 con una serie de vértices extras, por el teorema de Kuratowski sabemos que es
topológicamente complejo (ver la sección sobre grafos para más detalles).
o
o
o
2
1
3
4
5
Figura 8. La molécula de Simmons–Paquette es topológicamente compleja
En 1982, Walba, Richards y Haltiwanger [WRH] sintetizaron una molécula con la
forma de una escalera de Möbius con tres peldaños. El grafo de esta molécula está
formado por una cadena de poliéter de 60 átomos, entre carbonos y oxígenos (los
átomos de hidrógeno se omiten), que representa el borde de la cinta, y por tres enlaces
dobles que vienen a ser los peldaños de la escalera de Möbius.
o
o
o
o
o
o
o
o
c
o
3
1
2
o
o
o
o
o
o
a
o
o
o
b
Figura 9. Molécula con forma de escalera de Möbius con tres peldaños
La escalera de Möbius con tres peldaños es topológicamente compleja, lo que se
deduce del teorema de Kuratowski al contener un grafo bipartido K3,3 con una serie de
vértices extra (ver la sección sobre grafos).
Ya en 1975, Graf y Lehn [GL] sintetizaron una molécula cuyo grafo es una escalera
de Möbius con dos peldaños. En cambio, este grafo no es topológicamente complejo, tal
y como ilustra la siguiente figura:
7
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Figura 10. La escalera de Möbius con dos peldaños no es topológicamente compleja
Sin embargo, no fue hasta 1989 cuando se sintetizó la primera molécula con forma
de nudo. La síntesis de esta molécula fue lograda por Dietrich–Buchecker y Sauvage
[DS]. Compuesta por un total de 124 átomos, tiene la forma de un nudo trébol.
o
o
o
o
o
o
o
N
N
N
N
N
N
N
N
o
o
o
o
o
o
o
Figura 11. Una molécula con forma de nudo trébol
Más recientemente se han sintetizado muchas otras moléculas cuyos grafos
moleculares son topológicamente complejos, incluyendo nudos y enlaces. Por ejemplo,
en 1994 y 1995 Liang y Mislow ([LM]) descubrieron que muchas proteínas contienen
de modo natural grafos K3,3 y K5 , y nudos y enlaces.
Simetría especular de las moléculas
Nuestro trabajo se centra en el estudio de la simetría especular de nudos y enlaces
moleculares. Un tipo muy importante de estereoisomería química aparece cuando dos
moléculas topológicamente complejas tienen la misma fórmula química, pero su
estructura espacial es diferente, siendo una la imagen especular de la otra.
Cuando una molécula es diferente de su imagen especular decimos que es quiral
(chiral en inglés). El término procede del griego cheir, que significa mano. Nuestras
manos ofrecen el ejemplo por antonomasia de quiralidad: siendo la mano izquierda la
imagen especular de la derecha, no hay modo de superponerlas.
8
Isomería topológica
Figura 12. Las manos como ejemplo típico de quiralidad
Se llaman enantiómeros a un par de moléculas con la misma fórmula química pero
diferente fórmula desarrollada. Dos moléculas quirales que son una la imagen especular
de la otra son ejemplos de enantiómeros. El primero en observar la existencia de
enantiómeros fue Pasteur, en 1848. Al hacer atravesar un rayo de luz polarizada (aquel
en el que las ondas de la luz viajan todas en un mismo plano) a través de cristales de
ácido tartárico, observó como éste se desviaba en una u otra dirección. En general,
cuando la luz polarizada atraviesa una solución de alguna sustancia ópticamente activa,
es decir, que contiene un solo tipo de enantiómero de una molécula quiral, los rayos de
luz se desvían todos hacia la derecha, o todos hacia la izquierda. El enantiómero que
desvía la luz a la derecha recibe el nombre de dextro o D, y el que desvía la luz hacia la
izquierda es llamado levo o L.
Es importante resaltar que dos enantiómeros, además de por su actividad óptica,
pueden diferenciarse también por otras propiedades (por ejemplo, la limonada y la
naranjada son enantiómeros con sabores distintos). Un desgraciado ejemplo de esto fue
lo acontecido en los años 60 con la droga Talidomida, la cual se comercializó como una
mezcla racémica (de ambos enantiómeros) para tratar los mareos que suele sufrir la
mujer embarazada. Mientras que el enantiómero levo era el que curaba los mareos, el
enantiómero dextro causaba defectos en el feto. La razón por la que este tipo de
sustancias se comercializa como una mezcla racémica es puramente económica, ya que
resulta mucho más costoso producir una sustancia que contenga un solo tipo de
enantiómero. Debido al peligro potencial de estas mezclas, muchas compañías
farmacéuticas están empezando a producir sus medicamentos como sustancias puras.
Reconocimiento de la simetría vía el polinomio de Jones
Los matemáticos han desarrollado técnicas que ayudan a determinar cuando un nudo o
un enlace L es distinto de su imagen especular. La técnica utilizada en este proyecto es
el llamado polinomio de Jones VL(t), y más en concreto, el análisis de sus coeficientes
extremos. El polinomio de Jones, cuya variable denotamos con la letra t, se calcula
siguiendo las siguientes reglas:
 VU (t) = 1 si U es el nudo trivial.
 t 1 VL+ (t)  t VL- (t) + (t 1/2  t1/2 ) VL0 (t) = 0
si L+, L– y L0 son tres enlaces idénticos salvo en el entorno de un punto, donde se
distinguen según la siguiente figura:
9
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
L+
L_
L0
Figura 13. Diferencia local entre los enlaces L+, L– y L0
Cada nudo o enlace tiene asociado su correspondiente polinomio de Jones. Si dos
enlaces son equivalentes, entonces sus polinomios de Jones coinciden. Pero el recíproco
no es necesariamente cierto. De hecho, aún se desconoce si existe algún nudo distinto
del nudo trivial cuyo polinomio de Jones sea 1.
Como ejemplo, desarrollaremos el cálculo del polinomio de Jones para el caso de
dos nudos triviales disjuntos. Para ello se escogen como enlaces L+, L– y L0 los
siguientes (obsérvese que tanto L+ como L– son el nudo trivial, y L0 corresponde al
enlace cuyo polinomio de Jones queremos obtener):
L+
L_
L0
Figura 14. Cálculo del polinomio de Jones del enlace formado por dos nudos triviales disjuntos
Según las reglas para el cálculo del polinomio de Jones, se tiene
t 1 VL+ (t)  t VL- (t) + (t 1/2  t1/2 ) VL0 (t) = 0 .
Como L+ = L– es el nudo trivial, cuyo polinomio de Jones es 1, se sigue que
t 1  t  (t 1/2  t1/2 )VL0 (t)  0 ,
de donde
VL0 (t) =
t  t 1
=  t 1/2  t1/2 .
t 1/2  t1/2
Basta cruzar nuestros brazos delante de un espejo para darse cuenta de que la
imagen especular K* de un nudo K se obtiene invirtiendo cada cruce del diagrama de K.
El polinomio de Jones de K* se obtiene del de K sustituyendo t por t–1. En particular, si
el polinomio de Jones de un nudo K no es simétrico respecto al intercambio de t con t–1,
el nudo es distinto de su imagen especular. Por ejemplo, el polinomio de Jones del nudo
trébol K que aparece a la izquierda de la siguiente figura es VK (t) = t + t3 – t4, que no es
simétrico en la variable t. Deducimos entonces que su imagen especular (el nudo trébol
10
Isomería topológica
que aparece a la derecha de la figura, cuyo polinomio de Jones sería VK* (t) = t–1 + t–3 –
t–4) es un nudo diferente.
Figura 15. El nudo trébol K y su imagen especular K* son nudos diferentes
Coeficiente extremo del polinomio de Jones y teoría de grafos
A partir de un nudo o enlace K puede obtenerse un grafo GK (no confundir con el grafo
molecular) siguiendo un proceso de suavización de los cruces mediante A–cuerdas. Hay
tres pasos en este proceso:
Paso 1. Cada cruce del nudo se suaviza mediante una A–cuerda. Esto es, recorriendo el
nudo, cada vez que se pase por la parte vista de un cruce (“puente”) se gira hacia la
izquierda y se sigue por la parte que era la no vista del cruce (“túnel”), sustituyendo
dicho cruce por una cuerda (que pintamos en azul).
Figura 16. Paso 1, suavización por A–cuerdas
Lo descrito se muestra en el ejemplo de la siguiente figura, partiendo de un enlace
(de tres componentes) con seis cruces:
Figura 17. Ejemplo del Paso 1
11
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
El dibujo final de las A–cuerdas se ha realizado “estirando” éstas con objeto de
exagerar la figura para que se visualice con mayor claridad.
Paso 2. Eliminamos las A–cuerdas cuyos extremos están en diferentes componentes (en
general estas componentes, a las que llamaremos circunferencias de referencia, las
pintaremos de color negro). En nuestro ejemplo no tenemos A–cuerdas que eliminar, al
haber sólo una circunferencia de referencia.
Paso 3. El grafo GK es ahora construido de acuerdo a las siguientes reglas:
1. Cada cuerda es representada por un vértice del grafo.
2. Si dos cuerdas alternan sus extremos en una circunferencia de referencia,
entonces los dos vértices correspondientes son adyacentes.
3. Si dos cuerdas no alternan sus extremos en una circunferencia de referencia,
entonces los dos vértices correspondientes no son adyacentes.
Obviamente, el número de vértices del grafo GK es siempre menor o igual que el
número de cruces del nudo o enlace K. En el ejemplo que venimos desarrollando el
grafo GK que se obtiene es el hexágono, como puede verse en la siguiente figura:
Figura 18. Paso 3, del diagrama de A–cuerdas al grafo GK
La importancia del grafo GK construido a partir del nudo K radica en el hecho de
que cierto número I(GK) asociado al grafo, y que llamaremos independencia promedio
de éste, coincide quizás salvo signo con uno de los coeficientes extremos aM del
polinomio de Jones VK(t) del nudo K. Si en el proceso anterior suavizamos mediante B–
cuerdas (ver siguiente figura), se obtiene (quizás salvo signo) el otro coeficiente del
polinomio de Jones.
Figura 19. Suavización por B–cuerdas
12
Isomería topológica
Supongamos pues que deseamos conocer la posible quiralidad de un nudo o enlace
molecular K. A partir de K construimos, según los pasos ya explicados, un grafo GK
mediante suavización por A–cuerdas, y calculamos su independencia promedio I(GK).
Usando B–cuerdas, obtenemos un nuevo grafo y podemos calcular así una segunda
independencia promedio (se obtendría lo mismo calculando la independencia promedio
del grafo obtenido por suavización mediante A–cuerdas a partir del enlace K*). Si el
valor absoluto de ambas independencias promedio es distinto, podemos concluir
entonces que la molécula original es quiral. En efecto, en tal caso el polinomio de Jones
VK(t) del enlace K no sería simétrico en la variable t, ya que sus coeficientes extremos
serían distintos, y en consecuencia el nudo no presentaría simetría especular.
El siguiente esquema resume la idea que acabamos de detallar:
MOLÉCULA
POLINOMIO
DE JONES
DEL NUDO K
VK(t) =amtm+...+aMtM
NUDO O ENLACE
MOLECULAR
K
TEOREMA
aM = ± I(GK)
am = ± I(GK*)
CONSECUENCIA
Si | I(GK) | ≠ | I(GK*) |, entonces la
molécula no presenta simetría especular
GRAFO
GK
GRAFO
GK*
I(GK)
I(GK*)
INDEPENDENCIAS
PROMEDIO
En el resto de este trabajo desarrollamos el concepto de independencia promedio de
grafos y analizamos el problema abierto consistente en encontrar, para cada número
natural n, el grafo convertible (esto es, del tipo GK) con menor número de vértices
posible e independencia promedio n.
13
2. TEORÍA DE GRAFOS
Un grafo G está formado por un conjunto V de vértices y un conjunto E de aristas
constituido por pares no ordenados de vértices distintos. Así que en esta definición no
son aceptados los llamados bucles.
Del par de vértices que define una arista se dice que son los extremos de dicha
arista. Dos vértices se dicen adyacentes si existe una arista que los tiene por extremos.
Se llama grado de un vértice al número de aristas que lo tienen por extremo.
En nuestros grafos no aceptaremos aristas paralelas, esto es, dos aristas con los
mismos extremos.
Un camino en un grafo G es una sucesión ordenada de aristas, de modo que dos
aristas consecutivas comparten un vértice. Se suele decir que un camino conecta a sus
vértices extremos; éstos son el vértice de la primera arista que no lo es de la segunda, y
el vértice de la última arista que no lo es de la penúltima.
Un grafo G se dice que es conexo cuando para cualesquiera dos vértices del grafo
existe siempre un camino que los conecta.
Sea G un grafo con m vértices y v1, v2, …, vm una ordenación de sus vértices. La
matriz de adyacencia A = (aij) de G es una matriz booleana cuadrada de orden m
definida por la siguiente condición:
1 si los vértices vi y vj son adyacentes
aij =
0 en otro caso
Un grafo G es bipartido si el conjunto de vértices V de G puede escribirse en la
forma V = V1
V2 siendo V1  V2 = , de manera que cada arista de G tiene un
extremo en V1 y otro extremo en V2. Si V1 tiene k vértices y V2 tiene n vértices,
decimos que V es bipartido de tipo (k,n).
Sea G un grafo bipartido de tipo (k,n). En la matriz de adyacencia de G,
seleccionamos las k columnas correspondientes a los k vértices de V1 y las n filas
correspondientes a los n vértices de V2. Las entradas de la matriz de adyacencia que
están al mismo tiempo en una fila y en una columna de las seleccionadas constituyen la
llamada submatriz de adyacencia para el grafo bipartido G. Consideremos, por
ejemplo, el grafo G de la siguiente figura, seleccionando como V1 el conjunto de los
vértices azules y como V2 el conjunto de los vértices rojos:
1
2
4
3
Figura 20. Un grafo bipartido
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
En este caso la matriz de adyacencia es
R1
A1
R2
A2
R3
A3
R4
R1 A1 R2 A2 R3 A3 R4
0
1
0
0
0
0
0
1
0
1
0
0
0
1
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
0
1
0
1
0
0
0
1
0
y la submatriz de adyacencia es
R1
R2
R3
R4
A1 A2 A3
1
0
0
1
1
0
0
1
1
1
0
1
Sean G1 y G2 dos grafos y V1 y V2 sus respectivos conjuntos de vértices. Se dice que
G1 y G2 son grafos isomorfos si existe una función f: V1  V2 biunívoca tal que  v, w
∈ V1, se tiene que v y w son adyacentes en G1 si y sólo si f(v) y f(w) lo son en G2. Si
dos grafos G1 y G2 son isomorfos, intercambiando filas y/o columnas de la matriz de
adyacencia de G1 puede obtenerse la matriz de adyacencia de G2.
Grafos convertibles
En una representación de un grafo conexo mediante arcos, los vértices del grafo se
dibujan como arcos en el plano cuyos extremos descansan en una circunferencia (de
referencia) fijada en el mismo plano, de modo que los arcos son disjuntos entre si y
disjuntos con la circunferencia salvo por los extremos. Debe además verificarse la
siguiente propiedad: dos vértices del grafo son adyacentes si y sólo si los extremos de
sus correspondientes arcos alternan en la circunferencia.
Vértice
Adyacencia
No adyacencia
=
=
=
Arco
Extremos alternantes
Extremos no alternantes
Un grafo G se dice convertible si cada una de sus componentes conexas puede ser
representada mediante arcos. Con otras palabras, un grafo convertible G es siempre del
tipo G = GK para algún enlace K, aunque este enlace K no es necesariamente único. Por
ejemplo, el cuadrado o el hexágono H son grafos convertibles, pero el triángulo no lo
es:
16
Teoría de grafos
x
x?
Figura 21. El cuadrado y el hexágono son grafos convertibles; el triángulo no
Denotaremos por Cn el grafo cíclico de n vértices, y por Ln el grafo lineal con n
vértices (y n–1 aristas). Ambos son mostrados en la siguiente figura:
n-1
n
1
3
1
2
3
2
n-2
n-1
n
Figura 22. Los grafos cíclico Cn y lineal Ln
Todo grafo Ln es convertible. En general, un ciclo es convertible si y sólo si tiene un
número par de vértices. Es decir, Cn es convertible si y sólo si n es par. La siguiente
figura muestra la representación estándar mediante cuerdas de un ciclo Cn:
17
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
n-1
1
n
2
3
Figura 23. Representación estándar del ciclo Cn
Los grafos convertibles son ejemplos de grafos bipartidos. Esto parece claro si nos
fijamos en su representación mediante arcos; un subconjunto de vértices es el que se
corresponde con los arcos que quedan en la zona interior de la circunferencia, y el otro
subconjunto es el que se corresponde con los que quedan en la parte exterior.
Como ya hemos notado antes, los grafos convertibles son los grafos bipartidos que
se obtienen a partir de un nudo o enlace mediante una suavización por A–cuerdas. Por
esto, a lo largo de este proyecto trabajaremos siempre con grafos bipartidos. Los
vértices serán coloreados en azul o rojo, y se denotarán con las letras A y R
respectivamente, seguidas del número correspondiente de vértice.
Sobre grafos no planos y el teorema de Kuratowski
En la sección primera se definió un grafo topológicamente complejo como aquel grafo
sumergido en el espacio que no puede deformarse a un plano, aun asumiendo completa
flexibilidad.
El teorema de Kuratowski asegura que un grafo abstracto es no plano (es decir, no
admite ninguna representación plana) si y sólo si contiene un grafo isomorfo a un K5 (el
grafo completo de 5 vértices, es decir, un grafo con 5 vértices en el que cada par de
vértices está conectado por una arista) o a un K3,3 (el grafo bipartido en 3 y 3 vértices
con todas las aristas posibles), con la posible adición de vértices extras.
Figura 24. Los grafos K5 y K3,3
Por ejemplo, el grafo sumergido en R3 mostrado a la izquierda de la siguiente figura
es topológicamente complejo, aunque como grafo abstracto coincide con el grafo de la
derecha de la misma figura, que es plano.
18
Teoría de grafos
Figura 25. Una inmersión topológicamente compleja de un grafo plano
En la sección anterior afirmamos que la molécula de Simmons–Paquette o la
escalera de Möbius con tres peldaños son grafos topológicamente complejos. De hecho,
como grafos abstractos, son no planos, como puede deducirse del teorema de
Kuratowski.
19
3. INDEPENDENCIA PROMEDIO DE GRAFOS
En esta sección se define el concepto de independencia promedio de grafos y se repasa
una serie de herramientas conocidas para su cálculo.
Definición de I(G)
Se dice que un subconjunto de vértices C de un grafo G es independiente si no contiene
dos vértices adyacentes. Se llama independencia promedio de un grafo G, denotado
por I (G), al número entero
I(G)= (-1)|C|
C
donde C recorre la familia de subconjuntos independientes de vértices. En esta fórmula
|C| representa el cardinal de C, esto es, el número de vértices que hay en C.
Es decir, asociando a cada subconjunto de vértices independiente de G el valor 1 si
su cardinal es par, y –1 si es impar, la independencia promedio I(G) se obtiene sumando
todos estos valores.
Como ejemplos, en las siguientes tablas calculamos I(Ln) para los valores de n desde
1 hasta 6.
Para el vértice aislado L1:
|C|
0
1
C

{1}
Contribución (1)|C|
1
1
Contribución total
1
–1
0
C

{1},{2}
No hay
Contribución (1)|C|
1
–1
1
Contribución total
1
–2
0
–1
C

{1},{2},{3}
{1,3}
No hay
Contribución (1)|C|
1
–1
1
–1
Contribución total
1
–3
1
0
–1
Para L2:
|C|
0
1
2
Para L3:
|C|
0
1
2
3
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Para L4:
C

{1},{2},{3},{4}
{1,3}, {1,4}, {2,4}
No hay
No hay
Contribución (1)|C|
1
–1
1
–1
1
Contribución total
1
–4
3
0
0
0
C

{1}, {2}, {3}, {4}, {5}
{1,3}, {1,4}, {1,5}, {2,4}, {2,5}, {3,5}
{1,3,5}
No hay
No hay
Contribución (1)|C|
1
–1
1
–1
1
–1
Contribución total
1
–5
6
–1
0
0
1
Contribución (1)|C|
1
–1
Contribución total
1
–6
1
10
–1
1
–1
1
–4
0
0
0
1
|C|
0
1
2
3
4
Para L5:
|C|
0
1
2
3
4
5
Para L6:
|C|
0
1
2
3
4
5
6
C

{1}, {2}, {3}, {4}, {5}, {6}
{1,3}, {1,4}, {1,5}, {1,6}, {2,4}, {2,5},
{2,6}, {3,5}, {3,6}, {4,6}
{1,3,5}, {1,3,6}, {1,4,6}, {2,4,6}
No hay
No hay
No hay
Así que I(L1) = I(L4) = 0, I(L2) = I(L3) = –1 e I(L5) = I(L6) = 1.
Leyes para el cálculo de I(G)
En la práctica el cálculo de la independencia promedio de un grafo se ve facilitado por
el uso de una serie de herramientas que se describen a continuación:
Ley de recursión
I (G) = I (G – v) – I (G – Nv).
En esta fórmula el grafo G – v se obtiene suprimiendo en G el vértice v y sus aristas
incidentes, y el grafo G – Nv se obtiene a partir de G suprimiendo el vértice v, sus
aristas incidentes, los vértices adyacentes a v y sus aristas incidentes.
22
Independencia promedio de grafos
v
G
G-v
G - Nv
Figura 26. Los grafos G, G – v y G – Nv
Ley de multiplicación
I(G1 G2) = I(G1) · I(G2).
En esta fórmula G1 G2 denota la unión disjunta de los grafos G1 y G2. La ley de
multiplicación dice que la independencia promedio de una unión disjunta de grafos es el
producto de sus respectivas independencias promedio.
Figura 27. Grafos G1, G2 y su unión disjunta G1 ∪ G2
Ley de duplicación
Si Nv ⊂ Nw entonces I (G) = I (G – w).
En esta fórmula Nv es el conjunto de vértices adyacentes a v y Nw es el conjunto de
vértices adyacentes a w. Si Nv está contenido en Nw, decimos que el vértice w duplica
al vértice v. Así que la ley de duplicación permite suprimir cualquier vértice que
duplique sin que se vea afectada la independencia promedio del grafo.
v
w
Figura 28. El vértice w duplica al vértice v
23
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Ejemplo 1. En el grafo lineal Ln el vértice n – 2 duplica al vértice n, así que, por la ley
de duplicación
I(Ln) = I(Ln–3 L2),
y por la ley de multiplicación
I(Ln) = I(Ln–3) · I(L2) = –I(Ln–3).
Se sigue que I(Ln) = I(Ln–6). En consecuencia, la independencia promedio de un grafo
lineal es siempre –1, 0 ó 1, y la secuencia dada por las independencias promedio de L1
hasta L6 se repite hasta el infinito cada seis posiciones.
Ejemplo 2. Tomamos un vértice arbitrario v de Cn. La ley de recursión nos dice que
I(Cn) = I(Cn – v) – I(Cn – Nv) = I(Ln–1) – I(Ln–3).
En consecuencia I(Cn) sólo puede ser –2, –1, 1 ó 2, repitiéndose también cada seis
posiciones.
24
4. GRAFOS CON INDEPENDENCIA PROMEDIO
ARBITRARIA
El problema matemático objetivo de este proyecto es encontrar, para cualquier número
natural n, un grafo G convertible cuya independencia promedio I(G) sea n, teniendo G
el menor número de vértices posible.
En un artículo conjunto, Yongju Bae y Hugh R. Morton [BM] originalmente
propusieron el problema de encontrar, para cualquier número natural n, un grafo
convertible G cuya independencia promedio fuese n. Una solución a este problema
aparece en [M], donde para cada natural n se construye, usando como pieza básica el
hexágono, un grafo convertible Gn–1 con 6(n – 1) vértices e independencia promedio n.
En esta sección aportamos soluciones en donde el número de vértices del grafo es,
en general, considerablemente menor. Nuestras construcciones se basan en una forma
hábil de pegar las soluciones Gn dadas en [M], de modo que la pieza básica sigue siendo
el hexágono. Analizaremos en primer lugar los grafos Gn construidos en [M],
comenzando con algunas definiciones, construcciones básicas y resultados aportados en
dicho artículo.
La solución Gn–1 y otras construcciones conocidas
De ahora en adelante, escribiremos Gv para abreviar el par (G,v) donde G es un grafo y
v es un vértice particular elegido en G. Decimos que Gv es un ladrillo de tipo (n, k) si
I(G) = n e I(G – v) = k.
El hexágono H con la elección de cualquiera de sus vértices es un ejemplo de
ladrillo de tipo (2,1). En efecto, I(H) = I(L5) – I(L3) = 1– (–1) = 2 e I(H – v) = I(L5) =1.
Describimos ahora la construcción básica que utilizaremos en algunos ejemplos, a la
que llamaremos construcción estrella: sean G y F dos grafos y v y w dos vértices de G
y F respectivamente. Entonces Gv * Fw denotará al nuevo grafo obtenido de la unión
disjunta de G y F uniendo mediante una arista extra los vértices v y w (ver figura).
Nótese que si G y F son convertibles, entonces Gv * Fw también lo es.
v
G
w
v
w
F
Figura 29. Gv, Fw y la construcción estrella Gv * Fw
El resultado clave es el siguiente: sea G un grafo y v un vértice de G. Si Gv es un
ladrillo de tipo (n, k), entonces G1v1 es un ladrillo de tipo (n+k, k), donde G1 = Gv * Hw y
v1 es un vértice de H adyacente a w (ver figura).
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
v
w
v1
H
G
Figura 30. Si Gv es un ladrillo de tipo (n, k), entonces
(G v * H w )v1 lo es de tipo (n+k, k)
De este resultado puede deducirse (ver [M]) que el grafo Gr dibujado en la siguiente
figura tiene independencia promedio r+1. El grafo Gr se ha construido partiendo de un
hexágono y aplicando la construcción estrella r – 1 veces con nuevos hexágonos del
modo adecuado. De hecho G rv es un ladrillo de tipo (r+1, 1).
v
Figura 31. El grafo Gr (r hexágonos) tiene independencia promedio r+1
Si consideramos, por ejemplo, el caso I (G) = 41, la solución G40 tendrá 6 x 40 =
240 vértices. A continuación recordamos una construcción dada en [M] que permite
encontrar soluciones con menor número de vértices para algunas independencias
promedio.
Sean G1v1 , … , G kv k una serie de grafos con un vértice escogido vi  Gi para cada i
entre 1 y k. Denotaremos por S = S ( G1v1 , … , G kv k ) el grafo mostrado en la siguiente
figura, y lo llamaremos construcción simple. Podemos definir S de modo preciso
usando la construcción estrella: si w es el único vértice de L1, entonces
S = (( ... ((Lw1 * G1v1 )w * G2v2 )w * ... ) w ) * Gkvk .
vi
w
Gi
Figura 32. Construcción simple
26
Grafos con independencia promedio arbitraria
Si cada pieza Gi es un grafo convertible, entonces la construcción simple S también
lo es. Además puede probarse que I(S) = ∏ni – ∏ki si G iv i es un ladrillo de tipo (ni, ki).
El grafo Gv de la siguiente figura es un ladrillo de tipo (5, 3):
v
Figura 33. Un ladrillo de tipo (5, 3)
En consecuencia, la construcción simple S = S (Gv, Gv, Hw) (ver siguiente figura)
tiene independencia promedio (5  5  2)  (3  3  1)  50  9  41 . Esto es, su
independencia promedio coincide con la de G40, pero mientras que G40 tiene 240
vértices, S sólo tiene 43 vértices.
Figura 34. Un grafo G con I (G) = 41. Tiene 43 vértices
Nuestra mejora de la solución
En esta sección se aporta una solución con menos vértices que la dada en [M].
Supongamos en primer lugar que m no es un número primo, y sea m = ∏ki su
descomposición en factores primos ki. Para cada número primo ki consideramos el grafo
Gki -1 formado por ki – 1 hexágonos y cuya independencia promedio es ki. Denotaremos
por Nm la construcción simple realizada con los grafos Gki -1 y dos grafos L2, sin
importar los vértices que se seleccionan para realizar dicha construcción. En la siguiente
figura se muestran los grafos N4, N6 y N8.
27
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
w
w
w
Figura 35. Los grafos N4, N6, y N8
Teorema 1
La independencia promedio de Nm es m, es decir, I(Nm) = m.
En efecto, por la ley de recursión aplicada al vértice central w de la construcción
simple se tiene que I(Nm) = I(Nm – w) – I(Nm – Nw).
Por la ley de multiplicación I(Nm – w) = ∏ I( G k i 1 ) (I(L2))2 = ∏ki (–1)2 = ∏ki = m.
Por último, I(Nm – Nw) = 0 ya que Nm – Nw contiene vértices aislados.
Observar que las piezas extras L2 conducen a la existencia de vértices aislados (así
que a independencia promedio cero) al eliminar Nw. El utilizar dos de estas piezas ha
tenido por objeto la cancelación del signo al suprimir el vértice w.
En el caso en que m es un número primo distinto de dos, consideraremos la
descomposición m+1 = ∏pi en factores primos pi de m+1. Nótese que si m es primo
entonces m+1 no lo es, excepto para m = 2. Consideramos los grafos G pi 1
correspondientes, y en cada uno de ellos seleccionamos un vértice vi, de manera que
cada G pvii 1 sea un ladrillo de tipo (pi, 1). Esto se consigue tomando como vi un vértice de
un hexágono extremo adyacente al vértice por el que el hexágono se engancha con el
resto del grafo G pi 1 . Denotaremos por Ñm la construcción simple realizada con los
grafos G pi 1 con la precaución de utilizar los vértices vi seleccionados. En la siguiente
figura se muestran Ñ3, Ñ5, Ñ7 y Ñ11:
28
Grafos con independencia promedio arbitraria
w
w
w
w
Figura 36. Los grafos Ñ3, Ñ5, Ñ7 y Ñ11
Teorema 2
La independencia promedio de Ñm es m, es decir, I(Ñm ) = m.
En efecto, I(Ñm – w) = ∏ I( G pi 1 ) = ∏pi = m+1, y por otro lado I(Ñm – Nw) =
∏I( G pi 1 – vi) = 1, ya que G pvii 1 es un ladrillo de tipo (pi, 1). En consecuencia I(Ñm ) =
m por la ley de recursión.
Comparativa de las soluciones
La siguiente tabla compara los números de vértices del grafo Gm-1 aportado en [M] con
los grafos Nm y Ñm construidos en este proyecto, para independencias promedio m hasta
30. En la última columna hemos aplicado la misma construcción para independencias
promedios que no son números primos, siempre y cuando dicho número más uno
tampoco sea primo (la cifra de vértices aparece entonces en azul):
29
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Independencia m
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Número de vértices en…
Gm-1
Nm
Ñm
6
12
13
18
17
24
19
30
23
36
19
42
23
25
48
29
31
54
35
60
25
66
29
72
43
78
47
37
84
41
25
90
29
96
31
102
35
108
37
114
41
49
120
53
67
126
71
132
37
138
35
49
144
53
79
150
83
156
49
162
53
168
43
174
47
De forma general el número de vértices de las construcciones analizadas viene dado
por las siguientes fórmulas:
El número de vértices de Gm–1 es 6 (m – 1).
El número de vértices de Nm es 6 Σ (ki – 1) + 5, si m es no primo y m = ∏ki es su
descomposición en factores primos.
El número de vértices de Ñm es 6 Σ (pi – 1) + 1, si m es primo y m+1 = ∏pi es la
descomposición en factores primos de m+1.
En cualquier caso, el número de vértices de Nm ó Ñm es menor que el de Gm-1.
Observar por ejemplo que para m = 14, 15, que no son números primos, la solución
Ñm tiene menos vértices que Nm.
Más aún, ya que en la solución Nm no importa la elección de los vértices con los que
se realiza la construcción simple (no es necesario tener en cuenta el concepto de
30
Grafos con independencia promedio arbitraria
ladrillo), podrían utilizarse como “piezas” de esta construcción las soluciones dadas por
Ñm para números primos. Por ejemplo, para m = 14, podemos realizar la construcción
simple con los grafos G1 y Ñ7 sin olvidarnos del par de L2. El grafo obtenido tiene
independencia promedio 14 y sólo 30 vértices, menos que los 47 vértices de N14 o los
37 de Ñ14. Mostramos en la siguiente figura este grafo:
Figura 37. Una variación del grafo N14 con menos vértices que N14 y Ñ14
31
5. ANALIZANDO CUÁNDO UN GRAFO ES
CONVERTIBLE
Al investigar qué grafo convertible con menor número de vértices tiene por
independencia promedio un determinado número entero n, una dificultad importante
que se presenta es la de decidir cuando un grafo en cuestión es o no convertible.
Intentando salvar este escollo, hemos descubierto algunas propiedades que debe cumplir
todo grafo convertible, y cuya verificación se puede llevar a cabo de un modo mecánico
y razonablemente sencillo.
En esta sección analizamos estas propiedades, si bien es importante recalcar que la
caracterización completa de los grafos convertibles es todavía una cuestión abierta.
Comenzamos por introducir el concepto de ciclo puro, que jugará un papel básico en
todas las propiedades que estudiaremos.
Ciclos puros
Sea G un grafo y sea X = {v1, v2, … , vn} un subconjunto de vértices de G. Decimos que
X es un ciclo puro si X junto con todas las aristas que unen dos vértices cualesquiera de
X constituyen exactamente un ciclo.
Por ejemplo, en la siguiente figura los vértices coloreados de rojo forman un ciclo
puro en el grafo F; sin embargo en G no son un ciclo puro, ya que sus vértices y las
aristas que unen dos cualesquiera de los mismos no forman únicamente un ciclo.
F
G
Figura 38. Los vértices rojos constituyen un ciclo puro en F; no así en G
La observación clave relacionada con el concepto de ciclo puro es el hecho de que,
si X es un ciclo puro en un grafo convertible G, entonces existe una representación de G
mediante cuerdas, de manera que el ciclo constituido por los vértices de X aparece
representado de la manera estándar (ver figura 23).
Esta idea puede ser usada para probar que un determinado grafo no es convertible.
Por ejemplo, el grafo G8,2 mostrado en la siguiente figura no es convertible:
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Figura 39. El grafo G8, 2
Para probarlo considérese el conjunto X de los seis vértices que forman un
hexágono regular. Claramente X es un ciclo puro, así que si G8,2 fuese convertible,
podríamos dibujarlo de modo que el ciclo X se representase de la manera estándar:
Figura 40. Los vértices de X, representados de modo estándar
Como puede observarse ahora, no existe la forma de añadir los dos vértices
restantes, uno rojo y otro azul, respetando las alternancias. Por ejemplo, no hay modo de
hacer alternar el vértice azul con los vértices rojos del hexágono.
La idea de este ejemplo es generalizada en el siguiente teorema:
Teorema del vértice triple
Sea X un ciclo puro dentro de un grafo G y sea v un vértice de G. Si hay al menos tres
vértices de X adyacentes a v, entonces G no es convertible.
Obsérvese que de las hipótesis se deduce que el vértice v no pertenece al ciclo X.
Índices de conexión de dos ciclos
Sean C1 y C2 dos ciclos incluidos en un grafo G, de modo que su intersección sea
exactamente un grafo Lk. Llamaremos índices de conexión de C1 y C2 a los números
naturales i, j, k definidos así:
i = (número de vértices de C1) – k + 2,
j = (número de vértices de C2) – k + 2,
k = número de vértices de Lk.
34
Analizando cuándo un grafo es convertible
En el ejemplo de la siguiente figura los ciclos C1 y C2 tienen en común exactamente
un subgrafo L6. Los índices de conexión de C1 y C2 son 12, 11 y 6. El mismo grafo
puede ser visualizado también como dos ciclos de 21 y 15 vértices e intersección un L11
o como dos ciclos de 21 y 16 vértices con intersección un L12.
C1
C2
Figura 41. Dos ciclos cuya intersección es un único grafo lineal Lk
Observar que si G es un grafo convertible, entonces la paridad de los índices de
conexión es la misma (todos pares o todos impares). En efecto, en tal caso los ciclos C1
y C2 tienen un número par de vértices y en consecuencia si k es par, i y j también lo son,
y si k es impar, así lo son i y j.
Teorema de los índices de conexión
Sean C1 y C2 dos ciclos puros incluidos en un grafo G cuya intersección es un único
grafo Lk, k ≥ 1. Supongamos también que C = C1 C2 – {vértices no extremos de Lk}
es un ciclo puro. Entonces, si G es convertible, se verifica que al menos un índice de
conexión es menor o igual que tres.
Figura 42. Los tres ciclos en rojo deben ser puros para poder aplicar el teorema de los índices de
conexión
35
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
DEMOSTRACIÓN
Supongamos que a, b, c, … son los vértices ordenados de la intersección Lk = C1 ∩ C2,
tal y como muestra la siguiente figura:
z

C1
a
c
C2

b
Figura 43. Demostración del teorema de los índices de conexión
Al ser C1 un ciclo puro, si G es convertible existe una representación de G mediante
cuerdas con C1 representado del modo estándar:
a
 b
c
Figura 44. Única opción para la A-cuerda  (salvo simetría)
La cuerda que representa al vértice  (único vértice de C2 – Lk adyacente al vértice
a), no puede tener uno de sus extremos en el arco de circunferencia verde, ya que
alternaría con otro vértice de C1, contradiciendo el hecho de que C es un ciclo puro. Así
que las posibilidades para el vértice  son dos, la de la figura y otra simétrica.
Ahora bien, si una cuerda que representa a un vértice de C2 – Lk abandona (o sea,
tiene un solo extremo en) el arco de circunferencia acotado por la cuerda que representa
al vértice b, alternaría con éste y daría lugar, dado que C2 es un ciclo puro, a un índice
de conexión igual a 2 (el grafo L2 formado por los vértices a y b).
36
Analizando cuándo un grafo es convertible
Finalmente, si ninguna cuerda abandona el arco de circunferencia acotado por b, a lo
sumo éstas llegan a alternar con c, dando lugar a un índice de conexión igual a 3 (el
grafo L3 formado por los vértices a, b y c), o como última posibilidad, alternan con el
vértice a, lo que generaría un índice de conexión igual a 1 (con un único vértice a). Esto
concluye la demostración.
A continuación se muestra un grafo cuya no convertibilidad es deducible del
teorema de los índices de conexión. El lector puede encontrar dos ciclos puros
satisfaciendo las hipótesis del teorema y cuyos índices de conexión son todos mayores
que tres.
Figura 45. El teorema de los índices de conexión muestra que este grafo no es convertible
El siguiente grafo no es convertible, pero esto no puede deducirse ni del teorema del
vértice triple ni del teorema de los índices de conexión. Los vértices rojos constituyen
un ciclo puro, así que si el grafo fuese convertible admitiría una representación
mediante cuerdas como se muestra a la derecha de la figura. Observar entonces que una
de las cuerdas correspondiente a los vértices x e y no es dibujable.
x
x
y
Figura 46. Aplicación del teorema de perpendicularidad: el grafo de la figura no es convertible
La idea del ejemplo anterior es generalizada en el siguiente resultado:
Teorema de perpendicularidad
Sea C un ciclo puro incluido en un grafo G. Sean v1, v2, v3 y v4 cuatro vértices de C no
consecutivos, encontrados en este orden al recorrer C en algún sentido. Sean x e y dos
vértices no adyacentes entre sí y no pertenecientes a C, siendo v1 y v3 vértices
adyacentes a x, v2 y v4 vértices adyacentes a y. Entonces G es un grafo no convertible.
37
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
DEMOSTRACIÓN
Si G fuese convertible, existiría una representación de G mediante cuerdas con C
representado de la forma estándar, al ser C un ciclo puro incluido en G.
Más aún, el hecho de que G fuese convertible lo haría un grafo bipartido,
distinguiendo vértices rojos y azules, o equivalentemente a nivel de cuerdas, entre
cuerdas interiores y exteriores respecto a la circunferencia de referencia.
Como los vértices v1 y v3 son adyacentes a x, tienen necesariamente el mismo color.
Igualmente v2 y v4 comparten color. Se sigue que o los cuatro vértices tienen el mismo
color, o el color de v1 y v3 es distinto al de v2 y v4. Más aún, en la representación
mediante cuerdas encontraremos las cuerdas correspondientes a los vértices v1, v2, v3 y
v4 en este orden, digamos al recorrer la circunferencia de referencia en sentido contrario
al del movimiento de las agujas del reloj. En consecuencia se presentan dos
posibilidades, reflejadas en la siguiente figura:
v
v
v
x
v
v
x
v
v
x
v
v
v
v
v
Figura 47. Demostración del teorema de perpendicularidad
Es entonces sencillo observar que no podemos dibujar la cuerda correspondiente al
vértice y, una vez que hemos representado la correspondiente al vértice x. En efecto, en
el caso representado a la izquierda de la figura, la cuerda correspondiente al vértice y
cortaría a la correspondiente al vértice x; en el caso representado a la derecha de la
figura, dibujada por fuera la haría alternar con la cuerda correspondiente a x,
contradiciendo el hecho de que x e y son vértices no adyacentes.
Por último la hipótesis de que los vértices no sean consecutivos tiene por objeto
descartar la siguiente situación:
1
x
v3
y
v2
v4
Figura 48. Los cuatro vértices del teorema de perpendicularidad no pueden ser consecutivos
38
Analizando cuándo un grafo es convertible
La siguiente figura muestra un ejemplo concreto en que se ve la necesidad de la
hipótesis de que los vértices v1, v2, v3 y v4 no sean consecutivos en el ciclo puro C, en el
teorema de perpendicularidad. En este caso, C es el ciclo constituido por los vértices
azules:
Figura 49. Los vértices del ciclo puro deben ser no consecutivos en el teorema de perpendicularidad
Un grafo convertible es necesariamente bipartido. Además, si contiene un ciclo, éste
debe tener un número par de vértices. Más aún, si contiene dos ciclos cuya intersección
es exactamente un grafo lineal, la paridad de los índices de conexión correspondientes
debe ser la misma.
En esta sección hemos estudiado también una serie de resultados más específicos
que permiten deducir que ciertos grafos no son convertibles. A saber, el teorema del
vértice triple, el teorema de los índices de conexión y el teorema de perpendicularidad.
A continuación se muestra un ejemplo de grafo no convertible cuya no
convertibilidad no es deducible mediante ninguno de los criterios y resultados
anteriores:
A
A
Figura 50. Un grafo no convertible, que no cumple las hipótesis de los teoremas estudiados
Para ver que este grafo es no convertible dibujamos primero el ciclo puro formado
por los vértices azules del modo estándar (si el grafo fuese convertible admitiría una tal
representación). El modo de pintar el vértice A es ahora único, siendo imposible
representar el vértice restante.
Por último en esta sección, presentamos sin demostración una generalización del
teorema de perpendicularidad:
39
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Teorema general de perpendicularidad
Sea C un ciclo puro incluido en un grafo G. Sean v1, v2, v3 y v4 cuatro vértices de C de
grado tres no consecutivos, encontrados en este orden al recorrer C en algún sentido.
Supongamos que v1 y v3 son los extremos de un camino Lr (r  3) de modo que sus
vértices interiores tienen grado dos y ninguno es vértice de C. Igualmente, supongamos
que v2 y v4 son los extremos de un camino Ls (s  3) de modo que sus vértices interiores
tienen grado dos y ninguno es vértice de C. Entonces G no es convertible.
Usando este teorema también podemos deducir que el grafo de la figura anterior no
es convertible, considerando el ciclo puro formado por los vértices que aparecen en
azul, el vértice interior de Lr = L3 viene en rojo, los vértices interiores de Ls = L7 vienen
en verde:
v2
v1
v4
v3
Figura 51. Un grafo no convertible deducible del teorema general de perpendicularidad
40
6. GRAFOS CON POCOS VÉRTICES. PROGRAMACIÓN
En esta sección probaremos que las soluciones G1 y G2 con independencia promedio
dos y tres respectivamente, son las óptimas. Con precisión, probaremos que el hexágono
es el grafo convertible con menor número de vértices cuya independencia promedio es
igual a dos, y que no existe ningún grafo convertible con once o menos vértices e
independencia promedio tres, siendo así el grafo formado por dos hexágonos unidos
mediante la construcción estrella el representante más sencillo con independencia
promedio tres.
Recordar que todo grafo convertible es bipartido. Si la bipartición es del tipo (k,n),
siendo k el número de vértices azules y n el número de vértices rojos, ningún vértice
azul puede tener grado n, ya que duplicaría a cualquier otro vértice azul. Igualmente,
ningún vértice rojo puede tener grado k.
En nuestro estudio podemos prescindir también de cualquier grafo que contenga un
vértice con grado cero. En efecto, en tal caso el grafo tiene un vértice aislado, y por la
ley de multiplicación su independencia promedio es cero.
Así mismo, podemos prescindir de los grafos que tienen un vértice de grado uno, ya
que entonces dicho vértice está duplicado y por tanto existe un grafo con igual
independencia promedio y un vértice menos. La excepción a esta regla son los grafos
que tienen a L2 como una de sus componentes conexas. Por la ley de multiplicación, la
eliminación de un tal L2 conlleva un cambio de signo en la independencia.
En particular, no es necesario considerar las biparticiones de tipo (0,n), (1,n) ó (2,n).
En el caso de una bipartición (2,n), cualquiera de los n vértices rojos duplica, asumiendo
que los vértices azules no tienen grado cero o uno.
Estas observaciones muestran que no hay un grafo con independencia promedio dos
que tenga menos de seis vértices, y entre los grafos convertibles con seis vértices, sólo
la bipartición (3,3) puede dar lugar a independencia promedio dos. Más aún, cada
vértice ha de tener grado dos. En consecuencia, salvo isomorfismo, la única submatriz
de adyacencia posible es
R1
R2
R3
A1 A2 A3
1
1
0
1
0
1
0
1
1
Hemos rellenado los unos en la matriz de manera ordenada por columnas, de modo
que al colocar un 1 en una columna, lo hacemos siempre en la primera fila que se pueda
(en general, en el proceso de construcción de estas matrices se irán descartando aquellas
que, por intercambios de filas y/o columnas, resulten isomorfas).
El grafo que corresponde a dicha matriz es el hexágono, de independencia promedio
dos. Así pues, hemos demostrado el siguiente resultado:
Teorema
El hexágono es el único grafo convertible con seis o menos vértices que tiene
independencia promedio dos.
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Figura 52. El hexágono H = G1
Independencia promedio tres
El estudio de la independencia promedio de grafos de más de seis vértices da lugar,
sobre todo a partir de los diez y once vértices, a un elevado número de casos, para los
que se antoja tedioso el cálculo a mano de su independencia promedio. Por esta razón,
para el análisis sistemático de estos casos nos hemos valido de dos programas
desarrollados con MATLAB. Estos programas aparecen escritos y comentados al final
de esta sección.
El análisis realizado hasta ahora nos permite también asegurar que no existen grafos
convertibles con seis o menos vértices, que tengan independencia promedio tres o
menos tres. De hecho, |I(G)| es menor o igual que dos para todo grafo convertible G con
seis o menos vértices. Analizamos ahora los grafos con siete o más vértices.
Grafos con siete vértices
Bipartición (4,3) El hecho de que todo vértice azul deba tener grado dos produce
duplicación:
A1 A2 A3 A4
R1 1
1
0
*
R2 1
0
1
*
R3 0
1
1
*
Grafos con ocho vértices
La bipartición (5,3) lleva a duplicación con más motivo que la bipartición (4,3) del
apartado anterior. Nos queda pues analizar la bipartición (4,4).
Bipartición (4,4) En este caso todo vértice tiene grado 2 ó 3. Sea T el número de
vértices de color azul con grado 3.
 Caso T = 0. Se verifica que en cada columna y en cada fila hay exactamente dos unos.
Lo segundo es debido a que, si hubiese una fila con tres unos, tendríamos al menos una
fila con un uno como mucho (en total hay ocho unos en la matriz), y por tanto un vértice
rojo con grado uno o cero.
En primer lugar, observar que las operaciones de intercambio entre filas y entre
columnas no modifican el hecho de que cada fila y cada columna contengan
exactamente dos unos.
Por intercambio de columnas podemos colocar un 1 en la entrada (1,1), escogiendo
como primera columna una que tenga un 1 en la parte superior (hay dos tales columnas).
A continuación intercambiamos la fila dos con la única fila posterior que tiene un 1 a la
izquierda, para colocar un 1 en la entrada (2,1). Un nuevo intercambio de columnas, que
no involucre a la columna uno, coloca un 1 en la entrada (2,2). El otro 1 de la columna
dos debe estar en la tercera fila o posteriores; de lo contrario habría duplicación.
42
Grafos con pocos vértices. Programación
Continuando este proceso alternando intercambios de filas y columnas, y asumiendo
que no hay duplicación, obtenemos la submatriz de adyacencia siguiente, que se
corresponde con el ciclo octógono C8, con independencia promedio –1:
R1
R2
R3
R4
A1 A2 A3 A4
1
0
0
1
1
1
0
0
0
1
1
0
0
0
1
1
El siguiente ejemplo ilustra lo explicado, usando primero intercambio de columnas
(primera y segunda) y después intercambio de filas (segunda y tercera):
R1
R2
R3
R4
A1 A2 A3 A4
0
1
0
1
1
0
1
0
1
1
0
0
0
0
1
1
R1
R2
R3
R4
A1 A2 A3 A4
1
0
0
1
0
1
1
0
1
1
0
0
0
0
1
1
R1
R2
R3
R4
A1 A2 A3 A4
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
1
R1
R2
R3
R4
A1 A2 A3 A4
1
0
0
1
1
1
0
0
0
1
1
0
0
0
1
1
 Caso T = 1.
es la única submatriz de adyacencia posible. El grafo asociado G8,1, con independencia
promedio 0, es el siguiente:
2
3
4
1
2
3
1
Figura 53. El grafo G8,1 tiene independencia promedio cero
 Caso T = 2. No es posible construir la submatriz de adyacencia sin duplicaciones:
R1
R2
R3
R4
A1 A2 A3 A4
1
1
0
*
1
1
0
*
1
0
1
*
0
1
1
*
43
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
 Caso T = 3. Se produce igualmente duplicación:
A1 A2 A3 A4
1
1
1
*
1
1
0
*
1
0
1
*
0
1
1
*
R1
R2
R3
R4
 4
 Caso T = 4. Ya que hay   = 4 formas de colocar tres unos en cada una de las cuatro
3
columnas, la única matriz posible salvo isomorfismo es
A1 A2 A3 A4
1
1
1
0
1
1
0
1
1
0
1
1
0
1
1
1
R1
R2
R3
R4
El grafo asociado G8,2 tiene independencia promedio I(G8,2) = 3, pero ya hemos
visto anteriormente que este grafo no es convertible:
Figura 54. El grafo G8,2 tiene independencia promedio tres, pero no es convertible
Grafos con nueve vértices
La bipartición (6,3) conduce a duplicación, con más motivo que las biparticiones (5,3) ó
(4,3) de los apartados anteriores.
Bipartición (5,4) Como ya se ha visto anteriormente, podemos asumir que ningún
vértice azul tiene grado 0, 1 ó 4. Sea T el número de vértices de color azul con grado 3.
 4
 Caso T = 0. Como todo vértice azul tiene grado 2 y hay 4 vértices rojos, tenemos  
 2
= 6 maneras de rellenar cada columna. A saber:
1
1
0
0
44
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
1
0
0
1
1
Grafos con pocos vértices. Programación
6
Al haber cinco vértices azules, el número de matrices diferentes es   = 6, cada
5
una de las cuales se obtiene al descartar una de las seis posibles columnas (la repetición
de una columna conlleva duplicación y el intercambio de columnas produce matrices
asociadas a grafos isomorfos). Las seis matrices se muestran a continuación; la quinta
tiene independencia promedio –1 y las otras cinco –2:
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
1
0
0
1
0
0
1
1
0
1
0
1
0
0
0
1
0
1
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
1
0
0
1
0
0
1
0
0
1
0
1
1
0
0
1
0
1
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
1
0
0
1
0
0
1
0
0
1
0
0
1
0
0
1
1
1
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
1
0
0
1
1
0
1
0
0
0
1
1
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
1
0
0
0
1
0
1
0
1
0
1
1
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
0
0
0
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
 Caso T = 1. En este caso hay necesariamente duplicación:
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
0
0
*
1
0
1
0
*
1
0
0
1
*
0
1
1
1
*
 Caso T = 2. Al igual que en el caso anterior no es posible la construcción de ningún
grafo sin que haya duplicación. En efecto, si A1 y A2 son adyacentes ambos a dos
vértices rojos (pongamos R1 y R2) y cada uno de ellos a otro distinto, entonces A3 sólo
tiene la posibilidad de ser adyacente a los vértices R3 y R4, agotando las posibilidades
para los vértices azules A4 y A5:
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
0
*
*
1
1
0
*
*
1
0
1
*
*
0
1
1
*
*
45
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
 Caso T = 3. La situación es análoga a los dos casos anteriores:
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
1
*
*
1
1
0
*
*
1
0
1
*
*
0
1
1
*
*
 Caso T = 4. El vértice A5 no puede ser adyacente a dos vértices rojos sin ser
duplicado por alguno de los otros vértices azules:
R1
R2
R3
R4
A1 A2 A3 A4 A5
1
1
1
0
*
1
1
0
1
*
1
0
1
1
*
0
1
1
1
*
 4
 Caso T = 5. Como hay   = 4 maneras diferentes de colocar tres unos en cada
3
columna y hay cinco columnas a rellenar, no es posible construir una matriz sin que se
repitan columnas, lo que da lugar a duplicación.
Grafos con diez vértices
En la bipartición (7,3) se repite la situación que vimos en las biparticiones (4,3), (5,3) ó
(6,3) de los apartados anteriores.
Bipartición (6,4) Como ya se ha visto, ningún vértice azul puede tener grado 0, 1 ó 4.
Sea T el número de vértices azules con grado 3.
 Caso T = 0. Entonces todo vértice azul tiene grado dos. Al haber cuatro vértices rojos
 4
tenemos   = 6 maneras de rellenar cada columna. Como hay seis vértices azules la
 2
única submatriz de adyacencia posible es
R1
R2
R3
R4
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
El grafo G10, 1 que responde a esta representación matricial es
46
Grafos con pocos vértices. Programación
1
2
3
2
3
4
5
4
6
Figura 55. El grafo G10,1 tiene independencia promedio –3
Su independencia promedio es I (G10,1) = –3. Pero este grafo no es convertible, lo
que ya hemos visto como aplicación del teorema de perpendicularidad.
Los casos T = 1, 2, 3, 4, 5 y 6 conducen claramente a duplicación, según se muestra
esquemáticamente:
 Caso T = 1.
R1
R2
R3
R4
A1 A2 A3 A4 A5 A6
1
1
0
0
*
*
1
0
1
0
*
*
1
0
0
1
*
*
0
1
1
1
*
*
R1
R2
R3
R4
A1 A2 A3 A4 A5 A6
1
1
0
*
*
*
1
1
0
*
*
*
1
0
1
*
*
*
0
1
1
*
*
*
R1
R2
R3
R4
A1 A2 A3 A4 A5 A6
1
1
1
*
*
*
1
1
0
*
*
*
1
0
1
*
*
*
0
1
1
*
*
*
R1
R2
R3
R4
A1 A2 A3 A4 A5 A6
1
1
1
0
*
*
1
1
0
1
*
*
1
0
1
1
*
*
0
1
1
1
*
*
 Caso T = 2.
 Caso T = 3.
 Casos T = 4, 5 y 6.
47
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Bipartición (5,5) Los vértices pueden tener grado 2, 3 ó 4. Sean T y C los números de
vértices azules con grado tres y cuatro respectivamente.
5
 Caso C = 0, T = 0. Existen   = 10 formas diferentes de posicionar dos unos en cada
 2
10
columna. Como hay 5 columnas, el número total de matrices sería   = 252. Una de
5 
estas matrices es
A1 A2 A3 A4 A5
R1 1
0
0
0
1
R2 1
1
0
0
0
R3 0
1
1
0
0
R4 0
0
1
1
0
R5 0
0
0
1
1
El grafo que corresponde a esta representación matricial es el decágono, cuya
independencia promedio es I (C10) = –1.
Ahora bien, por un argumento análogo al analizado en el apartado de grafos con
ocho vértices, bipartición (4,4), caso T = 0, podemos deducir que el resto de matrices
son isomorfas a ésta o hay duplicación.
 Caso C = 0, T = 1. Tras rellenar las dos primeras columnas se observan dos
posibilidades diferentes:
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
0
1
0
1
0
0
1
0
1
b)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
1
0
0
1
0
0
En la posibilidad a, al elegir las adyacencias del vértice A3, éstas deberán ser
forzosamente un vértice rojo adyacente a A1 y otro que no lo sea, de manera que el
estudio se reduce al análisis del caso b por intercambio de columnas.
5
Las formas diferentes de rellenar cada columna son   = 10 y las posibilidades
 2
que vetan los dos primeros vértices azules son 4, por lo que el número de matrices
6
posibles es   = 20.
3
La independencia promedio de los grafos asociados a estas matrices oscila entre –2
y 1. Los cálculos se han realizado con el programa enumerartres.m.
 Caso C = 0, T = 2. Tras rellenar las dos primeras columnas se obtienen dos
posibilidades diferentes:
48
Grafos con pocos vértices. Programación
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
1
1
0
0
1
0
0
b)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
1
0
0
1
0
1
5
Caso b). En principio hay   = 10 formas de rellenar cada una de las tres
 2
columnas que quedan, debiendo restar las seis posiciones vetadas por los dos
primeros vértices azules para evitar duplicación. Al quedar tres vértices azules por
 4
rellenar, el número de matrices posibles es   = 4. Dichas matrices se muestran a
3
continuación; en los cuatro casos la independencia promedio de los grafos
correspondientes es –2:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
1
0
1
0
0
0
1
0
1
1
0
1
0
1
0
1
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
0
0
1
0
0
1
1
0
1
1
1
0
0
1
0
0
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
1
0
1
0
0
0
1
0
1
1
0
0
0
1
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
0
0
1
0
1
0
0
1
0
0
1
1
0
1
0
1
0
0
1
1
0
1
5
Caso a). En principio hay   = 10 formas de rellenar cada una de las tres columnas
 2
que quedan, debiendo restar las cinco posiciones vetadas por los dos primeros
vértices azules para evitar duplicación. Al quedar tres vértices azules por rellenar, el
5
número de matrices posibles es   =10. Los grafos asociados a estas matrices
3
tienen independencia promedio comprendida entre –2 y 1, salvo en el caso de la
matriz
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
0
1
1
0
El grafo correspondiente G10, 2 tiene independencia promedio I (G10,2) = –3. Más
interesante aún, G10,2 es convertible, como puede verse en la siguiente figura:
49
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
1
3
3
1
1
5
1
4
5
2
4
2
2
3
4
2
3
4
5
5
Figura 56. Un grafo convertible con diez vértices e independencia promedio –3
A continuación construimos un diagrama de un enlace a partir del cual se obtiene el
grafo G10,2 por el proceso de suavización de los cruces mediante A-cuerdas:
Figura 57. Construcción de un enlace asociado al grafo G10, 2
El diagrama obtenido es equivalente a un diagrama aparentemente más sencillo,
como se muestra en la siguiente figura:
Figura 58. Dos diagramas equivalentes
50
Grafos con pocos vértices. Programación
A continuación se muestra el grafo correspondiente a este enlace de ocho cruces; su
independencia promedio es 0 por tener vértices aislados:
Figura 59. El grafo obtenido a partir del diagrama “sencillo” tiene independencia promedio 0
En resumidas cuentas, tenemos dos diagramas de enlaces equivalentes que al ser
suavizados por A-cuerdas producen dos grafos distintos, uno con independencia
promedio –3 y otro 0. Aparentemente esto contradice el hecho de que los polinomios de
Jones de ambos enlaces coinciden, dado que la independencia promedios es, quizás
salvo signo, el coeficiente extremo aM de dicho polinomio.
Lo que ocurre es que, en general, aM = ±I(GK) con M = c + 2r – 2, siendo c el
número de cruces en el diagrama del enlace y r el número de circunferencias de
referencia en el diagrama de A-cuerdas. Y este es el coeficiente extremo de VK(t)
siempre y cuando no sea cero.
Para el primer diagrama tenemos c = 10, r = 1 así que M = 10, siendo I(GK) = –3.
Para el segundo diagrama tenemos c = 8, r = 4 así que M = 14, siendo I(G K) = 0. En
conclusión VK(t) = ... ± 3 t10. Aunque el segundo diagrama es aparentemente más simple
(de hecho, tiene menos cruces), es el primer diagrama el que permite encontrar el
coeficiente extremo del polinomio de Jones del enlace.
 Caso C = 0, T = 3. Obligatoriamente hay dos vértices azules que tienen en común dos
vértices rojos. Por intercambio de columnas y filas podemos entonces asumir que las
dos primeras columnas de la matriz son
R1
R2
R3
R4
R5
1
1
0
0
1
A1 A2 A3 A4 A5
1
1
1
1
1
0
0
1
0
0
 5
Para rellenar la tercera columna tenemos un total de   – 2 = 8 posibilidades:
 3
1
1
1
0
0
0
0
0
0
0
1
1
1
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1
1
Por intercambio de filas, usar la quinta columna equivale a usar la segunda, y usar la
cuarta, sexta o séptima equivale a usar la tercera. Quedan pues cuatro casos a analizar:
51
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
a)
R1
R2
R3
R4
R5
c)
A1 A2 A3 A4 A5
1
1
1
1
1
1
1
0
0
0
1
0
0
0
1
b)
A1 A2 A3 A4 A5
1
1
1
1
1
0
1
0
1
0
1
0
0
0
1
d)
A1 A2 A3 A4 A5
1
1
1
1
1
0
1
0
1
0
1
1
0
0
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
R1
R1 1
1
0
R2
R2 1
1
0
R3
R3 1
0
1
R4
R4 0
1
1
R5
R5 0
0
1
5
En los casos a y c, las posibilidades para las dos columnas restantes son   – 7 =
 2
3 (hay siete columnas vetadas por las tres primeras), de manera que el número de
3
matrices posibles es   = 3. En el caso b hay seis columnas vetadas, y por tanto un
 2
 4
total de   = 6 matrices. Finalmente, en el caso d las columnas vetadas son ocho; sólo
 2
existe una matriz.
De las trece matrices que pueden generarse en total, sólo encontramos una de
interés, que proviene del caso c:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
0
0
1
1
0
La independencia promedio del grafo asociado G10,3 es I (G10,3) = –3. Y, como puede
observarse en la figura, este grafo es convertible:
5
3
3
2
5
1
4
4
5
3
2
1
2
4
2
5
3
4
1
Figura 60. El grafo convertible G10,3 tiene diez vértices e independencia promedio – 3
52
Grafos con pocos vértices. Programación
Figura 61. Construcción de un nudo asociado al grafo G10, 3 (el nudo morado es un nudo trébol)
 Caso C = 0, T = 4. Son casos derivados del apartado C = 0, T = 3. Con el programa
enumerartres.m, tomando como X las tres primeras columnas de los casos a, b, c y d,
comprobamos que las independencias promedio que se obtienen oscilan entre –2 y 2.
 Caso C = 0, T = 5. Para cada uno de los casos a, b, c y d del apartado C = 0, T = 3,
 5
hay   – 3 = 7 formas de rellenar cada una de las dos últimas columnas, y por tanto
 3
7
 2  = 21 posibles matrices. Con el programa enumerartres.m hemos comprobado que
 
la independencia promedio de los grafos correspondientes a las 84 (4 por 21) matrices
están comprendidas entre –2 y 1.
 Caso C = 1, T = 0. La única matriz posible es la siguiente (el grafo asociado tiene
independencia promedio 2):
A1 A2 A3 A4 A5
R1 1
1
0
0
0
R2 1
0
1
0
0
R3 1
0
0
1
0
R4 1
0
0
0
1
R5 0
1
1
1
1
53
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
 Caso C = 1, T = 1. Este caso conduce a duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
0
*
1
1
0
0
*
1
0
1
0
*
1
0
0
1
*
0
1
1
1
*
 Caso C = 1, T = 2. Las dos posibilidades iniciales llevan a duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
*
1
1
0
0
*
1
0
1
0
*
1
0
0
1
*
0
1
1
1
*
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
0
*
*
1
1
0
*
*
1
0
1
*
*
1
0
1
*
*
0
1
1
*
*
 Caso C = 1, T = 3. Inicialmente tenemos las dos posibilidades anteriores:
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
1
1
0
1
0
1
1
0
0
0
1
1
b)
R1
R2
R3
R4
R5
A1 A2
1
1
1
1
1
0
1
0
0
1
A3
0
0
1
1
1
A4
A5
En el caso b, el vértice A5, con grado dos, está necesariamente duplicado. En el caso
a, el vértice A5 con grado dos debe ser adyacente a R4 y R5 para evitar ser duplicado, lo
que determina la siguiente matriz (el grafo correspondiente tiene independencia
promedio –1):
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
1
 Caso C = 1, T = 4. Al ser C = 1, el aspecto de la matriz es
R1
R2
R3
R4
R5
54
A1 A2 A3 A4 A5
1
1
1
1
0
1
1
1
1
Grafos con pocos vértices. Programación
En cada columna que queda por rellenar deben colocarse dos unos más, por lo que
 4
6
hay   = 6 columnas posibles y por tanto   = 15 posibles matrices. Las
 2
 4
independencias promedio de los grafos asociados a todas estas matrices oscilan entre –1
y 1, según hemos comprobado con enumerartres.m.
 Caso C = 2. La matriz es obligadamente de la forma
A1 A2 A3 A4 A5
R1
R2
R3
R4
R5
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
Si T no es tres, al menos uno de los vértices A3, A4 ó A5 está duplicado. Y si T = 3,
la duplicación se evita sólo si la matriz es de la forma
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
0
0
1
1
0
1
0
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
El grafo asociado a dicha matriz tiene independencia promedio 1.
 Caso C = 3. Hay necesariamente duplicación. Siendo la matriz obligadamente de la
forma que sigue, se veta cualquier vértice azul de grado dos, y sólo es posible uno de
grado tres, con columna 0,0,1,1,1:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
1
1
1
1
1
0
1
0
1
0
1
1
 Caso C = 4. No se puede completar la columna correspondiente al vértice A5 sin que
haya duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5
1
1
1
1
*
1
1
1
0
*
1
1
0
1
*
1
0
1
1
*
0
1
1
1
*
55
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
 Caso C = 5. La matriz es obligadamente de la forma
A1 A2 A3 A4 A5
R1
R2
R3
R4
R5
1
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
1
El grafo asociado a esta matriz tiene independencia promedio 4, aunque no es
convertible (se trata de un cono del grafo G8,2 en las hipótesis del teorema del vértice
triple).
Grafos con once vértices
La bipartición (8,3) conduce a duplicación, como las biparticiones (7,3), (6,3), (5,3) y
(4,3). En el análisis de las siguientes biparticiones, T y C denotan el número de vértices
azules de grado tres y cuatro respectivamente.
Bipartición (7,4) Siempre habrá duplicación. Por supuesto podemos asumir que todo
vértice azul tiene grado dos o tres. Por otro lado tenemos siete columnas a rellenar y
 4
 2  = 6 formas de rellenar una columna con dos unos. Si T = 1, tres de estas seis
 
posibilidades están vetadas por la columna correspondiente al vértice azul de grado tres,
y ninguna matriz es posible sin duplicación. Si T = 2 ó 3, el mismo argumento se aplica.
Si T 4, la duplicación es también obvia.
Bipartición (6,5)
 Caso C ≥ 3. Este caso siempre da lugar a duplicaciones. En efecto, fijadas las tres
primeras columnas, ninguno de los tres vértices azules restantes puede tener grado dos.
Un cuarto vértice azul con grado cuatro veta la posibilidad de que haya un vértice de
grado tres, y los tres vértices azules restantes no pueden tener todos grado cuatro pues
5
con cuatro unos sólo podemos rellenar   = 5 columnas. Por último, tampoco pueden
 4
tener grado tres pues A5 ya estaría duplicado.
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
1
1
1
0
1
0
1
0
1
1
 Caso C = 2. Tampoco existe la forma de construir un grafo sin duplicaciones. En
efecto, fijadas las dos primeras columnas, los vértices restantes deben ser todos
adyacentes a R4 y R5. En consecuencia cualquier vértice de grado dos estaría
duplicado. Ahora bien, sólo pueden colocarse tres vértices azules con grado tres; tras el
cuarto habría duplicación:
56
Grafos con pocos vértices. Programación
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
*
1
1
0
1
0
*
1
1
0
0
1
*
1
0
1
1
1
1
0
1
1
1
1
1
 Caso C = 1, T = 0. Da lugar a duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
0
0
*
1
0
1
0
0
*
1
0
0
1
0
*
1
0
0
0
1
*
0
1
1
1
1
1
 Caso C =1, T = 1. Da lugar a duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
0
*
*
1
1
0
0
*
*
1
0
1
0
*
*
1
0
0
1
*
*
0
1
1
1
1
1
 Caso C = 1, T = 2. En principio hay dos posibilidades diferentes, pero ambas
conducen obviamente a duplicación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
*
*
1
1
0
0
*
*
1
0
1
0
*
*
1
0
0
1
*
*
0
1
1
1
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
*
*
*
1
1
0
*
*
*
1
0
1
*
*
*
1
0
1
*
*
*
0
1
1
1
1
1
 Caso C = 1, T = 3. Asumiendo que A1 tiene grado cuatro y A5 y A6 grado dos, salvo
isomorfismo la matriz debe tener la forma que sigue, si se desea evitar la duplicación.
Entonces alguno de los vértices de grado tres (A2, A3 ó A4) duplica a A5 ó A6, o bien
los tres tienen exactamente los mismos vértices adyacentes:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
*
*
*
1
0
1
*
*
*
0
1
1
*
*
*
0
0
1
*
*
*
0
0
0
1
1
1
1
1
 Caso C = 1, T = 4. Podemos asumir que la matriz tiene la forma que sigue, siendo
imposible colocar dos unos más en las columnas segunda a quinta sin que se produzca
duplicación:
57
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
0
0
0
0
1
1
*
*
*
*
0
1
*
*
*
*
0
1
*
*
*
*
0
0
1
1
1
1
1
 Caso C = 1, T = 5. Por ser el vértice A1 de grado 4, se tiene la siguiente situación:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
1
1
1
1
1
 4
Hay   = 6 formas de rellenar cada una de las restantes columnas. Como quedan
 2
cinco columnas por rellenar, tenemos entonces seis posibles matrices (salvo
isomorfismo y evitando duplicación obvia). La independencia promedio de los grafos
correspondientes es en los seis casos –1.
 Caso C = 0, T = 0. Toda columna tiene entonces dos unos. En un principio pueden
pensarse dos situaciones diferentes:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
0
1
0
0
1
0
1
0
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
0
1
1
0
1
0
0
0
0
Ahora bien, el primer caso se reduce al segundo una vez rellenada la tercera
columna, por intercambio de filas y columnas. La independencia promedio de los grafos
asociados oscila entre –2 y 2 según hemos comprobado con el programa enumerartres.m
8 
(debemos considerar   = 70 matrices).
 4
 Caso C = 0, T = 1. Suponiendo que A1 es adyacente a R1, R2 y R3, debe haber un
vértice azul que tenga un vértice adyacente entre R1, R2 y R3 y el otro entre R4 y R5 (si
no es A2, lo será A3):
A1 A2 A3 A4 A5 A6
R1 1
1
R2 1
0
R3 1
0
R4 0
1
R5 0
0
58
Grafos con pocos vértices. Programación
5
Hay   = 10 formas de rellenar cada una de las cuatro columnas restantes. Como
2
 
6
 4
las posiciones vetadas por A1 y A2 son cuatro, tenemos   = 15 matrices. Se ha
comprobado con el programa enumerartres.m que las independencias promedio de los
grafos correspondientes oscilan entre –2 y 2.
 Caso C = 0, T = 2. Fijando las dos primeras columnas obtenemos dos posibilidades
diferentes:
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
0
1
0
1
b)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
0
0
1
0
0
En el caso a hay seis posiciones vetadas por las dos primeras columnas, y por tanto
5
  – 6 = 4 formas de rellenar cada una de las cuatro columnas restantes. En
 2
consecuencia sólo hay una matriz posible (el grafo asociado tiene independencia
promedio – 2):
A1 A2 A3 A4 A5 A6
R1 1
1
0
0
0
0
R2 1
0
1
1
0
0
R3 1
0
0
0
1
1
R4 0
1
1
0
1
0
R5 0
1
0
1
0
1
En el caso b hay cinco posiciones vetadas por las dos primeras columnas, y por
5
tanto   – 5 = 5 formas de rellenar cada una de las cuatro columnas restantes. En
2
 
consecuencia hay cinco matrices posibles de interés: cuatro de los grafos
correspondientes tienen independencia promedio –2 y uno tiene 0.
 Caso C = 0, T = 3. Al rellenar las dos primeras columnas nos encontramos con las
dos posibilidades del caso anterior:
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
0
1
0
1
b)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
0
0
1
0
0
En el caso a, según el vértice A3 sea o no adyacente a R1, podemos distinguir
(gracias al intercambio de filas y columnas) dos posibilidades:
59
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
a1)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
1
1
0
0
0
1
1
0
1
0
a2)
A1 A2 A3 A4 A5 A6
1
1
0
1
0
1
1
0
1
0
1
1
0
1
0
R1
R2
R3
R4
R5
5
En el caso a1, de las   = 10 formas de rellenar cada columna restante, siete están
2
 
vetadas por las tres primeras columnas. En consecuencia la matriz es única:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
0
1
0
0
1
0
1
0
1
El grafo asociado (ver siguiente figura) tiene independencia promedio –3, pero no es
convertible. Esto puede deducirse del teorema de los índices de conexión; los ciclos C1
y C2 (en rosa y verde respectivamente), y el ciclo “exterior” R3-A1-R1-A2-R5-A6 son
puros, siendo los tres índices de conexión correspondientes iguales a 4:
A1
R1
R2
A4
A3
R3
A6
A2
R4
A5
R5
Figura 62. Un grafo con independencia promedio –3 que no es convertible
Nótese que este grafo es no plano pues contiene, con algunos vértices extras, un
grafo K3,3 (A1, A2, A3 y R1, R2, R4 constituyen la bipartición necesaria).
En el caso a2 las posiciones vetadas son ocho, así que es imposible construir una
matriz sin duplicaciones.
 5
En el caso b distinguimos   – 2 = 8 formas de rellenar la tercera columna sin
 3
repetir ninguna de las dos primeras:
b1)
R1
60
A1 A2 A3 A4 A5 A6
1
1
1
b2)
R1
A1 A2 A3 A4 A5 A6
1
1
1
Grafos con pocos vértices. Programación
R2
R3
R4
R5
b3)
1
1
0
0
1
0
1
0
1
0
0
1
R2
R3
R4
R5
b4)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
0
1
0
1
0
1
0
0
0
1
b6)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
1
1
1
0
1
0
1
1
0
0
0
b8)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
1
1
1
0
0
0
1
1
0
0
1
b5)
b7)
1
1
0
0
1
0
1
0
0
1
1
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
0
1
0
0
0
1
1
0
0
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
1
1
1
0
1
0
1
0
0
0
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
1
0
1
0
1
0
1
1
0
0
1
5
En cada caso hay   = 10 formas diferentes de rellenar las tres columnas restantes.
2
 
En el caso b1 las posiciones vetadas son siete y la matriz que se produce es única:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
1
0
0
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
En el caso b2 existen cuatro matrices diferentes, obtenibles seleccionando tres de las
siguientes cuatro columnas:
1
0
0
0
1
0
1
0
0
1
A1 A2 A3 A4 A5 A6
R1 1
1
1
1
0
0
0
0
1
0
1
0
0
0
1
1
A1 A2 A3 A4 A5 A6
R1 1
1
1
1
0
0
61
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
R2
R3
R4
R5
R1
R2
R3
R4
R5
1
1
0
0
1
0
1
0
0
1
1
0
0
0
0
1
1
0
0
1
0
1
0
1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
0
0
1
0
0
0
1
1
1
R1
R2
R3
R4
R5
1
1
0
0
1
0
1
0
0
1
1
0
0
0
0
1
1
0
0
1
0
0
1
1
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
1
0
0
0
1
1
1
Para los casos b3 y b4 la posibilidad es única, obteniéndose respectivamente las
siguientes matrices:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
0
1
0
0
1
1
0
0
1
1
0
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
0
0
1
0
0
0
1
1
0
1
1
0
1
0
0
0
1
1
0
1
El caso b5 coincide con b2 intercambiando las filas primera y segunda; igualmente,
el caso b6 coincide con b3 y el caso b7 coincide con b4. Finalmente, el caso b8 no
produce ninguna matriz pues las tres primeras columnas vetan ocho posibilidades.
Se verifica que los grafos asociados a las siete matrices presentadas arriba tienen
independencia promedio igual a 0.
 Caso C = 0, T = 4. Como en el caso anterior, distinguimos las siguientes
posibilidades:
a)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
0
1
0
1
b)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
1
0
0
1
0
0
En el caso a podemos distinguir los siguientes subcasos:
a1)
R1
R2
R3
R4
R5
62
A1 A2 A3 A4 A5 A6
1
1
1
1
0
1
1
0
0
0
1
1
0
1
0
a2)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
0
1
1
0
1
0
1
1
0
1
0
Grafos con pocos vértices. Programación
5
Para el caso a1 hay   – 3 = 7 formas diferentes de rellenar la cuarta columna. Dos
3
 
de estas formas (las que corresponden a las columnas 0,1,1,0,1 y 0,0,1,1,1) vetan nueve
5
posibilidades de las   = 10 que hay para rellenar cada una de las dos columnas
 2
últimas; las otras cinco formas vetan exactamente ocho posibilidades, así que producen
cada una de ellas una matriz:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
0
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
0
1
0
0
1
0
1
0
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
0
1
1
1
0
0
0
1
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
0
1
0
1
0
1
0
1
0
0
1
0
1
0
1
1
0
0
1
0
1
0
1
1
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
0
1
1
1
0
1
0
0
1
0
1
0
1
1
1
0
0
0
1
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
0
1
1
0
0
1
0
0
0
1
1
0
1
1
1
1
0
0
1
0
1
0
1
El grafo G11,1 que corresponde a la cuarta matriz (ver siguiente figura) tiene
independencia promedio –4, pero no es convertible. Esto puede deducirse del teorema
del vértice triple, aplicado al vértice R1 y al ciclo puro A1–R2–A3–R4–A2–R5–A4–R3.
Los grafos correspondientes a las otras matrices tienen todos independencia promedio –
3. Ninguno de estos grafos es convertible, por el teorema del vértice triple; en el grafo
que corresponde a la primera matriz el ciclo puro es A2-R4-A3-R2-A4-R5, en el
segundo caso existe un ciclo puro formado por los vértices A1-R2-A3-R4-A4-R3, para
la tercera matriz se distingue el ciclo puro R2-A1-R3-A4-R5-A2-R4-A3, y en el último
de los casos localizamos otro ciclo puro A1-R2-A3-R4-A2-R5-A6-R3; en todos ellos el
vértice triple es R1.
63
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
6
4
3
2
1
1
2
4
5
3
5
Figura 63. El grafo G11,1 tiene independencia promedio –4 pero no es convertible
En el caso a2 las tres primeras columnas vetan ocho de las diez formas posibles de
rellenar cada una de las dos últimas columnas. En consecuencia existen sólo dos
matrices posibles:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
0
0
1
0
1
1
1
0
1
0
1
0
0
1
0
1
1
1
0
0
0
1
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
0
1
0
0
1
0
1
0
1
0
1
0
1
1
0
1
0
1
1
1
0
0
0
1
0
0
1
1
Los grafos correspondientes a ambas matrices tienen independencia promedio –3,
pero no son convertibles debido al teorema del vértice triple. En el primer caso el ciclo
puro es el formado por A1-R1-A4-R4-A3-R3 y el vértice triple es R2; en el segundo
caso el ciclo puro es A1-R1-A4-R4-A3-R2 y el vértice triple es R3.
5
Al estudiar el caso b observamos que hay   – 2 = 8 formas de rellenar la tercera
3
 
columna. Por intercambio de filas y columnas cinco de estas posibilidades se reducen a
los casos a1 y a2 ya tratados. Las tres formas restantes de rellenar la tercera columna,
1
1
0
1
0
1
0
1
1
0
1
1
1
0
0
dan también las que podemos usar para la cuarta columna, obteniendo las tres
posibilidades siguientes:
b1)
R1
R2
R3
R4
R5
64
A1 A2 A3 A4 A5 A6
1
1
1
1
1
1
1
0
1
0
0
1
0
1
0
1
0
0
1
0
b2)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
1
1
1
1
0
0
1
0
1
0
1
0
0
1
0
Grafos con pocos vértices. Programación
b3)
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
1
0
1
1
0
1
1
0
1
1
1
0
0
0
0
Notar que b1 y b2 son el mismo caso después de intercambiar la primera y segunda
fila. Las dos restantes columnas para b1 han de rellenarse con dos unos cada una, así
5
que hay   – 8 = 2 formas de rellenarlas. En consecuencia b1 (y b2) se completa de
 2
una única manera posible:
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
1
0
0
1
1
1
0
0
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
El grafo correspondiente tiene independencia promedio –3, pero no es convertible
por el teorema del vértice triple aplicado al ciclo puro A1-R1-A2-R4-A6-R5-A5-R3 y al
vértice A4.
5
En el caso b3 hay seis posibilidades vetadas, así que existen   – 6 = 4 formas de
2
 
 4
rellenar la quinta columna, y por tanto   = 6 posibles matrices:
2
 
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
1
1
0
1
0
1
1
0
1
1
0
0
0
1
1
1
0
0
0
0
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
1
1
1
0
0
0
0
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
0
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
1
0
1
0
1
1
0
1
0
1
1
1
0
0
0
0
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
1
0
1
0
1
1
0
0
0
1
1
1
0
1
0
0
0
0
1
1
R1
R2
R3
R4
R5
A1 A2 A3 A4 A5 A6
1
1
1
0
0
0
1
1
0
1
0
0
1
0
1
1
1
0
0
1
1
1
0
1
0
0
0
0
1
1
65
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Todos los grafos asociados a estas matrices tienen independencia promedio –3, pero
ninguno es convertible por el teorema del vértice triple aplicado (en todos los casos) al
ciclo puro A1-R3-A4-R4-A2-R1 y al vértice R2.
 Caso C = 0, T = 5. Podemos asumir que la única columna que corresponde al vértice
5
de grado dos es 1, 1, 0, 0, 0, la cual veta tres columnas con tres unos de las   = 10
3
7
5
posibilidades. Así pues, hay   = 21 matrices que pueden generarse.
La independencias promedio de los grafos asociados, calculadas con el programa
ind.m, es en todos los casos –3.
5
 Caso C = 0, T = 6. Sabemos que hay   = 10 formas diferentes de posicionar 3 unos
3
 
en columnas de cinco filas. Al haber 6 vértices azules, el número de matrices que
10
pueden generarse será   = 210. Las independencias promedio de los grafos
6 
asociados están comprendidas entre –2 y 1 (cálculos realizados con enumerartres.m).
Programación con MATLAB
En esta sección se muestran los programas informáticos que se han creado para facilitar
el cálculo de las independencias promedio de grafos a través de su representación
matricial.
El programa que se muestra a continuación calcula la independencia promedio de un
grafo introduciendo la submatriz de adyacencia asociada a él.
Fichero ind.m
%ind devuelve la independencia promedio
function I=ind(A)
if final(A)==1
I=ind1(A);
else
B=matrizB(A);
C=matrizC(A);
I=ind(B)-ind(C);
end
%final asigna un 1 a las matrices "finales" (matrices sin
filas o sin columnas)
function V=final(A)
[f,c]=size(A);
if f==0|c==0 %grafo con solo vertices aislados
V=1;
else V=0;
end
%ind1 devuelve 1 para las matrices sin filas ni columnas
%Devuelve 0 para todas las demas
66
Grafos con pocos vértices. Programación
function I=ind1(A)
[f,c]=size(A);
if f==0&c==0 %grafo vacio
I=1;
else I=0;
end
%matrizB aplicado a una matriz A elimina su primera fila
function B=matrizB(A)
[f,c]=size(A);
B=A(2:f,:);
%matrizC aplicado a una matriz A elimina su primera fila
%y las columnas j con A(1,j)=1
function C=matrizC(A)
[f,c]=size(A);
X=find(A(1,:)==0);
C=A(2:f,X);
El programa ind se va deshaciendo en cada paso del primer vértice rojo v = R1
mediante la ley de recursión. La fórmula
I (G) = I (G – v) – I (G – Nv)
se traduce, a nivel de submatrices de adyacencia, en la fórmula
I (A) = I (B) – I (C)
donde B = matrizB(A), es decir, A sin su primera fila, y C = matrizC(A), es decir, A sin
su primera fila y sin las columnas j tales que A(1,j) = 1, lo que se corresponde con la
eliminación
azules que eran adyacentes a R1.
R1 de los vértices
A1
R1
R1
A1
A1
R3
R3
R3
A2
A2
A2
R2
R2
R2
↔
A1 A2 A3
R1 1
1
0
R2 0
1
1
R3 1
0
1
=A
↔
A1 A2 A3
R2 0
1
1
R3 1
0
1
=B
↔
A3
R2 1
R3 1
=C
A3
A3
A3
A1
A1
A1
A2
A2
A2
R2
R2
R2
R3
R3
R3
A3
A3
A3
R3
R3
R3
R2
R2
R2
A3
A3
A3
Figura 64. Desarrollo del programa ind
67
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
Las matrices “finales” del proceso, es decir, aquellas que no tienen filas o no tienen
columnas, son tratadas mediante la instrucción
if final(A)==1
I=ind1(A);
En consecuencia:
 Si A es de orden 13, MATLAB considera la matriz B = matrizB(A) de
orden 03, aunque no tiene ninguna entrada. Por tanto final(B) = 1 e ind1(B) = 0, lo que
se corresponde con tener (tres) vértices aislados.
 Si A = (1 0 0), MATLAB considera la matriz C = matrizC(A) de orden 02
así que final(C) = 1 e ind1(C) = 0, lo que se corresponde con tener (dos) vértices
aislados.
 Finalmente, si A = (1 1 1) (en general una matriz fila con todos unos),
entonces MATLAB considera la matriz C = matrizC(A) de orden 00, así que final(C)
= 1 e ind1(C) = 1, lo que se corresponde con el grafo vacío.
Enumeración de matrices e independencia promedio
El siguiente programa enumera todas las matrices con número de independencia
promedio comprendida en un intervalo dado y presenta la posibilidad de fijar tantas
columnas como se desee. Además permite especificar el número de unos de aquellas
columnas que no se conozcan.
Fichero enumerartres.m
% enumerartres enumera las matrices que ademas de cumplir
ciertos requisitos
% tienen independencia promedio comprendida entre dos valores
dados
function E=enumerartres(X,n,A,i1,i2)
%
%
%
%
%
%
Inputs:
X una matriz booleana
A una matriz fila con entradas naturales
n es un natural que coincide con el numero de filas de X
Es necesario incluir n para que MATLAB acepte X=[]
i1 e i2 son dos enteros tales que i1<=i2
%
%
%
%
%
Output:
enumeracion de las matrices [X,P] con
independencia promedio en el intervalo [i1,i2]
siendo P una matriz booleana con las mismas filas que X
y con A(j) unos en su columna j
listado=sand(n,A);
%llama al programa sand.m
[ff,cf]=size(listado);
numeromatrices=ff/n;
for indice = 1:numeromatrices
A = [X,listado((n*(indice-1)+1):(n*indice),:)];
68
Grafos con pocos vértices. Programación
if
ind(A)<=i2
&
ind(A)>=i1
%Escribir
aqui
independencia de interes
(['la matriz ' num2str(indice) '-ésima es:'])
A = [X,listado((n*(indice-1)+1):(n*indice),:)],
disp('con independencia')
I=ind(A)
else
end
end
%sand
function listado=sand(n,A)
repematriz.m
%llama
a
los
programas
la
cus.m
[f,c]=size(A);
if c==1
[f1,c1]=size(cus(n,A(1)));
listado=reshape(cus(n,A(1)),f1*c1,1);
else listadoprevio=sand(n,A(1:c-1));
[fprevio,cprevio]=size(listadoprevio);x=(fprevio)/n;
t=A(c);
r=(factorial(n))/(factorial(t)*factorial(n-t));
listadopreviorepetido=repematriz(listadoprevio,r);
extra=reshape(repematriz(cus(n,t),x),n*r*x,1);
listado=[listadopreviorepetido,extra];
end
% cus
function lista = cus(long,t)
% crea una lista "lista" de
longitud "long" con t unos
las
sucesiones
booleanas
de
if (t == 0)
lista =zeros(long,1);
elseif (long == t)
lista =ones(long,1);
elseif (long < t)
disp('el numero t de unos supera a la longitud')
else
sublista1 = cus(long - 1,t-1);
%sucesiones a las que
añadir un uno
sublista2 = cus(long - 1,t);
%sucesiones a las que añadir
un cero
%las concateno con un cero, y luego con un uno
[filas1, columnas1] = size(sublista1);
[filas2, columnas2] = size(sublista2);
for i = 1 : long -1
for j = 1 : columnas1
lista(i,j)=sublista1(i,j);
lista(long,j)=1; %añado uno al final a la secuencia
de la sublista1
end
end
69
Independencia promedio de grafos y polinomio de Jones. Aplicaciones en ingeniería
for i = 1 : long - 1
for j = 1 : columnas2
lista(i,columnas1 + j)=sublista2(i,j);
lista(long,columnas1 + j)=0; %añado cero al final a
la secuencia de la sublista2
end
end
end
% repematriz
function N=repematriz(M,r)
N=M;
for k=1:r-1
Q=[N;M];
N=Q;
end
70
%repite r veces M verticalmente
7. CONCLUSIÓN
El presente proyecto expone una de las múltiples conexiones existentes entre las
matemáticas y la química, más en concreto, entre la teoría de nudos y grafos y la noción
de isomería molecular.
Para mostrar esta conexión, hemos realizado un pequeño repaso de los momentos
históricos más relevantes al respecto y explicado la herramienta matemática (polinomio
de Jones) que hace posible la relación entre estas ideas en principio de naturalezas
distintas.
Con este punto de partida, en el grueso del trabajo hemos analizado un problema
matemático relacionado con la independencia promedio de grafos, obteniendo algunas
respuestas creativas.
BIBLIOGRAFÍA
[BM] Bae, Y., Morton, H. R.: The spread and extreme terms of Jones polynomials.
Journal of Knot Theory and its ramifications, Vol. 12, 359-373, (2003).
[DS] Dietrich-Buchecker, C., Sauvage, J.–P.: A synthetic molecular trefoil knot.
Angew. Chem. Int. Ed. Engl. (1989), 189-192.
[F]
Flapan, E.: When topology meets chemistry: a topological look at molecular
chirality. Cambridge University Press, 2000.
[FW] Frisch, H., Wasserman, E.: Chemical topology. J. Am. Math. Soc. (1992), 223236.
[GL] Graf, E., Lehn, J.–M.: Synthesis and cryptate complexes of a spheroidal
macrotricyclic ligand with octahedrotetrahedral coordination. J. Am. Chem.
Soc. (1975), 5022-5024.
[LM] Liang, C., Mislow, K.: Topological chirality of proteins. J. Am. Chem. Soc.
(1994b), 3588-3592.
[M]
Manchón, P. M. G.: Extreme coefficients of the Jones polynomial and graph
theory. Journal of Knot Theory and its ramifications, Vol. 13, No. 2, 277-295
(2004).
[PV] Paquette, L. A., Vazeux, M.: Threefold transannular epoxide cyclization
synthesis of a heterocyclic C17-hexaquinane. Tetrahedron Lett. (1981), 291-294.
[SM] Simmons, H. E., Maggio, J. E.: Synthesis of the first topologically non-planar
molecule. Tetrahedron Lett. (1981), 287-290.
[WRH]Walba, D., Richards, R., Haltiwanger, R. C.: Total synthesis of the first
molecular Möbious strip. J. Am. Chem. Soc. (1982), 3219-3221.