Problemas Tema 3. Introducción al análisis de circuitos eléctricos

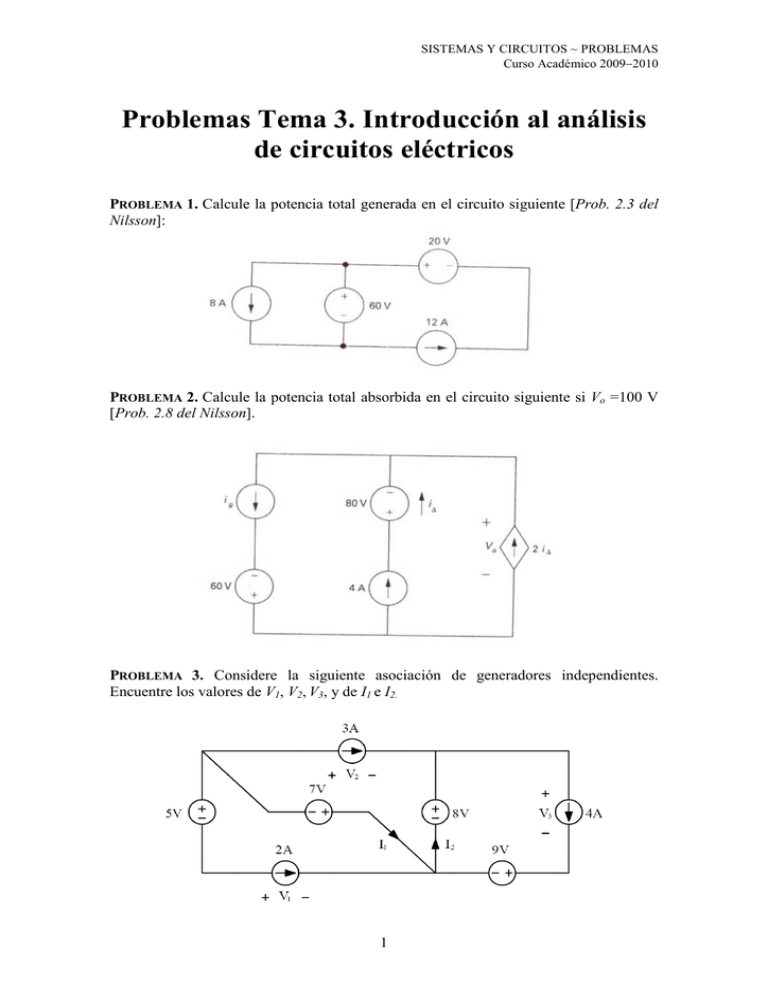
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
Problemas Tema 3. Introducción al análisis
de circuitos eléctricos
PROBLEMA 1. Calcule la potencia total generada en el circuito siguiente [Prob. 2.3 del
Nilsson]:
PROBLEMA 2. Calcule la potencia total absorbida en el circuito siguiente si Vo =100 V
[Prob. 2.8 del Nilsson].
PROBLEMA 3. Considere la siguiente asociación de generadores independientes.
Encuentre los valores de V1, V2, V3, y de I1 e I2.
1
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 4. Calcular la resistencia equivalente entre los terminales a y b de los
siguientes circuitos.
PROBLEMA 5. Considere el siguiente circuito donde los valores de los elementos son: R1
= 5 Ω, R2 = 4 Ω, R3 = 2 Ω, Ig = 15 A. Calcule los valores de I1 y I2 utilizando un divisor
de corriente.
PROBLEMA 6. Considere el siguiente circuito donde los valores de los elementos son: R1
= 1 Ω, R2 = 4 Ω, R3 = 2 Ω, Vg = 7 V. Calcule los valores de V1 y V2 utilizando un divisor
de tensión.
2
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 7. Calcule el valor de la tensión V y el de la corriente I en el siguiente
circuito y compruebe que se verifica el balance de potencias.
5V
2Ω
V
1Ω
10V
5Ω
28V
I
PROBLEMA 8. Calcule los voltajes y corrientes de todos los elementos del siguiente
circuito y compruebe que se verifica el balance de potencias. Los valores de los
elementos son: R1 = 3 Ω, R2 = 1 Ω, R3 = 2 Ω, Ig1 = 1 A, Ig2 = 3 A.
PROBLEMA 9. Resuelva (calcule las corrientes y potenciales) el circuito de la figura
siguiente.
1Ω
5Ω
147 V
2Ω
35 Ω
147 V
10 Ω
1Ω
PROBLEMA 10. En el circuito de la figura siguiente, calcule vo(t) e io(t).
2Ω
15 Ω
+
5Ω
4Ω
2Ω
i0(t)
5Ω
v0(t)
-
3
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 11. Utilice el método de tensiones de nodo para calcular v1(t) y v2(t) en el
siguiente circuito.
4Ω
80 Ω
+
10 Ω
+
v1(t)
5Ω
v2(t)
-
-
PROBLEMA 12. Utilice el método de corrientes de malla para calcular io(t) en el
siguiente circuito.
4Ω
3.2 Ω
16 Ω
i0(t)
0.8 Ω
5.6 Ω
PROBLEMA 13. Determine los valores de V e I en el siguiente circuito.
3Ω
V
12V
2Ω
4Ω
I
10V
2Ω
8V
3Ω
PROBLEMA 14. Calcule VO en el siguiente circuito..
4
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 15. Determine el valor de Vy en el siguiente circuito.
PROBLEMA 16. En el siguiente circuito, determine el valor de la corriente I que circula
por el generador de 25 V y la tensión V que cae en el generador de corriente de 1 A, con
las polaridades indicadas en la figura. [Septiembre 2003].
PROBLEMA 17. Calcule los equivalentes de Thévenin y Norton de los siguientes
circuitos; en el primer caso, con respecto a los terminales a y b y en el segundo caso,
con respecto a los terminales c y d.
c
2Ω
9A
12Ω
a
2Ω
9Ω
4Ω
9A
12Ω
9Ω
b
4Ω
d
5
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 18. Calcule el equivalente de Thévenin y Norton con respecto a los
terminales a y b del circuito siguiente.
PROBLEMA 19. Calcule el equivalente de Thévenin con respecto a los terminales A y B
del circuito siguiente.
PROBLEMA 20. En el circuito de la figura, encuentre I1, I2 y V1 y calcule la potencia que
suministran tanto la fuente de tensión como la fuente de corriente. [Febrero 2004].
6
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
PROBLEMA 21. Considere el circuito de la figura siguiente en el que R1 = 100 Ω, R2 =
100 Ω, R3 = 50 Ω, R4 = 50 Ω, Vg = 80 V y α = 0,1. [Septiembre 2006].
a) Calcule el valor de la tensión V∆, la corriente que circula por la resistencia R3
y la tensión en bornas del generador de corriente dependiente, V0.
b) Calcule el equivalente de Thévenin con respecto a los terminales a y b del
circuito.
c) Entre los terminales a y b del circuito se conecta una resistencia de carga, RL.
Calcule el valor de dicha resistencia para que la potencia total suministrada por
el circuito sea igual a 15 W. (Recuerde que puede sustituir el circuito anterior,
entre los terminales a y b, por su equivalente de Thévenin).
7
SISTEMAS Y CIRCUITOS ~ PROBLEMAS
Curso Académico 2009−2010
Soluciones
PROBLEMA 1. Pgenerada = -720 W.
PROBLEMA 2. Pabsorbida = 2240 W.
PROBLEMA 3. V1 = -12 V; V2 = -15 V; V3 = -1 V; I1 = -5 A; I2 = 1 A.
PROBLEMA 4. a) Req = 2 Ω; b) Req = 12 Ω.
PROBLEMA 5. I1 = 10 A; I2 = 5 A.
PROBLEMA 6. V1 = 3 V; V2 = 4 V.
PROBLEMA 7. V = -10 V; I = -3 A; Pabsorbida = 224 W. Pcedida = -224 W.
PROBLEMA 8. VR1 = 3 V; IR1 = 1 A; VR2 = 3 V; IR2 = 3 A; VR3 = 0 V; IR3 = 0 A; Vg1=3 V;
Ig1 = 1 A; Vg2 = 3 V; Ig2 = 3 A; Pabsorbida = 12 W. Pcedida = -12 W.
PROBLEMA 9. Corrientes: 21 A, 14 A, 7 A, 7 A, 28 A, 21 A; Potenciales: 28 V, 14 V,
21 V, 105 V, 140 V, 245 V.
PROBLEMA 10. vo(t) = 10 V; io(t) = 10 A.
PROBLEMA 11. v1(t) = 100 V; v2(t) = 20 V.
PROBLEMA 12. io(t) = 27 A.
PROBLEMA 13. V = 1,2 V; I = 0 A.
PROBLEMA 14. VO = 480 V.
PROBLEMA 15. Vy = 4,5 V.
PROBLEMA 16. V = -50 V; I = 5 A.
PROBLEMA 17. Primer caso: VTH = 36 V, RTH = 6 Ω, IN = 6 A, RN = 6 Ω; Segundo caso:
VTH = 60 V, RTH = 20/3 Ω, IN = 9 A, RN = 20/3 Ω.
PROBLEMA 18. VTH = 20 V, RTH = 5/8 Ω, IN = 32 A, RN = 5/8 Ω.
PROBLEMA 19. VTH = 20 V, RTH = 10/17 Ω.
PROBLEMA 20. I1 = -1,5 A; I2 = 3 A; V = 100 V; PVg = -220 W; PIg = -480 W.
PROBLEMA 21. a) V∆ = 10 V; IR3 = -0,4 A; V0 = -20 V; b) VTH = 30 V, RTH = 43,75 Ω;
c) RL = 16,25 Ω.
8