Tema 6: FLEXIÓN: DEFORMACIONES
Anuncio

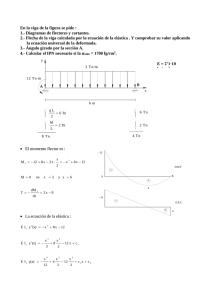
Tema 6: Flexión: Deformaciones Tema 6: FLEXIÓN: DEFORMACIONES x + y Prof.: Jaime Santo Domingo Santillana E.P.S.-Zamora – (U.SAL.) - 2008 1 Tema 6: Flexión: Deformaciones 6.1.- INTRODUCCIÓN Las deformaciones hay que limitarlas al igual que las tensiones, bien por razones de seguridad, de mantenimiento o simplemente de estética. Así, en numerosos casos, los elementos estructurales se dimensionarán aparte de a Resistencia, limitando sus tensiones máximas, (tal y como hemos visto en el tema anterior), a RIGIDEZ, haciendo que las deformaciones máximas no sobrepases unos determinados valores admisibles. En diferentes normativas se fijan los valores admisibles de las deformaciones para diferentes elementos estructurales. Con el estudio de las deformaciones de una viga a Flexión, calcularemos los GIROS (θz , θy ) que sufren las secciones transversales alrededor del eje neutro y las FLECHAS o DESPLAZAMIENTOS (y, z) de sus centros de gravedad. θz Flexión en plano xy Flexión en plano xz θy z z y x x y y z Fig.6.1 Los métodos que desarrollaremos para el cálculo de las deformaciones son los siguientes: • Método de la Ecuación Diferencial de la Línea Elástica • Método de la Ecuación Universal de la Línea Elástica • Método de los Teoremas de Mohr • Método energético del Teorema de Castigliano • Método energético de los Trabajos Virtuales Observación: Los dos métodos energéticos los estudiaremos más adelante, en el tema 9º, dado que son métodos de cálculo más generales y tienen su aplicación en el estudio de las deformaciones, no sólo a Flexión, sino también en los casos de Tracción, Compresión, Torsión, etc. 2 Sección 6.2: Método de la Ecuación Diferencial de la Elástica 6.2.-MÉTODO DE LA ECUACIÓN DIFERENCIAL DE LA ELÁSTICA Consideremos la viga de la figura sometida a Flexión Simple (Ry, Mz) x y Línea elástica x y = y(x) Fig.6.2 Según vimos en la sección 5.3.3. se denomina línea elástica: “al eje x de la viga (el que pasa por los centros de gravedad de todas las secciones transversales), una vez deformado”. Tratemos ahora de calcular su ecuación: y = y(x) Vimos también en dicha sección, que para el caso de Flexión Pura (sólo momentos flectores), el radio de curvatura de la línea elástica venía dado por la ecuación (5.20): 1 Mz = r E .I z pues bien, para el caso de la Flexión Simple (momentos flectores y fuerzas cortantes), podremos utilizar la misma fórmula del radio de curvatura, pues la influencia que ejercen las fuerzas cortantes es pequeña y la podremos despreciar en la mayoría de los casos. Por otra parte sabemos por Matemáticas que el radio de curvatura de una curva se puede obtener de la expresión: d2y 1 dx 2 = (6.1) r dy 2 3/ 2 1 + dx igualando las expresiones del radio de curvatura: d2y M dx 2 = z (6.2) 3 / 2 E .I z dy 2 1 + dx expresión obtenida que representa la “ecuación diferencial de la línea elástica” La integración de esta ecuación diferencial, no lineal, presenta grandes dificultades y dado que en la mayoría de los casos las deformaciones que se van a presentar, son pequeñas, podremos hacer las siguientes simplificaciones: 3 Tema 6: Flexión: Deformaciones θz x θz y = y(x) y tangente Fig.6.3 dy = tagϑz ≅ ϑz (para pequeñas deformaciones) → Giros de las secciones dx si las deformaciones son pequeñas: θz es pequeño → tag θz es pequeño → dy/dx es 2 dy pequeño → 1 + ≅ 1 y haciendo esta aproximación en la ecuación (6.2) quedará: dx 2 d y Mz d dy M dϑ z M z (6.3) o bien: = z → (6.4) = = 2 dx E .I z dx dx E.I z dx E.I z Observación: con el sistema de ejes coordenados adoptado en el tema 5.2 para las vigas a flexión, resultará que: si M z > 0 → si M z < 0 → d2y <0 dx 2 d2y >0 dx 2 En efecto, supongamos: Mz >0 x2 x1 x θ2 y tag1 θ1 tag2 Fig.6.4 si x2 > x1 → dx > 0 y además según se ve en la fig.6.4 : ϑ2 < ϑ1 → dϑ < 0 dϑ d2y < 0 o lo que es lo mismo : 2 < 0 dx dx y lo mismo se comprobaría para el caso: Mz<0. con lo cual se cumplirá : 4 Sección 6.2: Método de la Ecuación Diferencial de la Elástica En virtud de ello en las ecuaciones (6.3) y (6.4) deberemos introducir un signo (-) quedando finalmente como Ecuación diferencial de la línea elástica : M d2y =− z 2 E .I z dx (6.5) dϑ z M =− z dx E.I z o bien: (6.6) OBSERVACIONES: 1.- Integrando una vez la Ecuación diferencial de la línea elástica obtendremos los Giros θz (ver ecuación 6.6). Si integramos dos veces dicha ecuación obtendremos las Flechas y de los centros de gravedad de cada sección (ver ecuación 6.5) o lo que es lo mismo la Ecuación de la línea elástica: y = y(x) 2.- La ecuación de la línea elástica: y = y(x), es una función continua (ver figura 6.5.a). Si fuera discontinua (ver figura 6.5.b), es que se habría roto Fig.6.5.a Fig.6.5.b 3.- La ecuación de los giros: θz = θz (x), es también una función continua. Sería discontinua sólo si la elástica presentase un punto anguloso (ver fig.6.5.c) θ1 tag 1 θ2 tag tagθ21 punto anguloso Fig.6.5.c En un punto anguloso se ha de verificar: 1 =∞ r ,entonces la ecuación (5.20), antes 1 Mz = = ∞ y para que esto se cumpla → M z = ∞ . Pero r E.I z éste valor nunca se va a dar. mencionada, quedará: 4.- La ecuación diferencial de la elástica d2y será discontinua en los puntos en que dx 2 Mz sea discontinuo. 5 Tema 6: Flexión: Deformaciones 5.- Si en una sección de una viga es Mz = 0, la elástica presentará un punto de inflexión en dicho punto d2y M =− z =0 → 2 dx E .I z d2y = 0 → puntos de inflexión de la elástica y = y ( x ) dx 2 6.- Si la viga hubiese estado sometida a flexión simple en el plano xz: Rz, My, las ecuaciones diferenciales (6.5) y (6.6) de la elástica serían: My d 2z =− 2 E .I y dx dϑ y (6.7) dx =− My (6.8) E .I y 7.- Si la viga estuviese sometida a flexión en ambos planos: xy y xz habría que calcular por separado los giros y flechas relativos a ambos planos con las ecuaciones: (6.5), (6.6), (6.7), y (6.8) . A continuación se compondrían vectorialmente los giros: θz, θy y las flechas: y, z giro total: ϑ = ϑz + ϑ y ϑ = ϑ z2 + ϑ y2 flecha total: δ = y+z δ = y2 + z2 z Elástica en plano xx debida a la flexión My z y x δ y Elástica en plano xy debida a la flexión Mz Fig.6.6 6 Sección 6.3: Método de los Teoremas de Mohr 6.3.-MÉTODO DE LOS TEOREMAS DE MOHR Primer Teorema de Mohr: El primer teorema de Mohr nos permite calcular el ángulo θAB que forman entre sí dos secciones A y B de una viga flexionada. Éste ángulo será el mismo que el que forman las tangentes a la elástica en los puntos A y B θAB x θB A tag en B B y x θAB dx θA tag en A A B x Mz Mz Fig.6.9 La ecuación diferencial de la elástica es, según ecuación 6.6: dϑ z M =− z dx E .I z → dϑ z = − M z .dx E .I z e integrando esta ecuación entre los puntos A y B : B B M z .dx E .I z A ∫ dϑ z = − ∫ A B M z .dx E .I z A → ϑz ( B ) − ϑz ( A) = − ∫ o bien : B M z .dx E .I z A ϑ z ( AB ) = ϑ z ( A) − ϑ z ( B ) = ∫ (6.15) 7 Tema 6: Flexión-Deformaciones Caso particular: En el caso de que el módulo de rigidez de la viga sea constante: E.Iz = cte, la ecuación 6.15. se podrá expresar también de la siguiente manera: B B M .dx ϑz ( AB ) = ϑz ( A) − ϑz ( B ) = ∫ z = ( E .I z = cte) = E .I z A ∫M z .dx A E .I z S M AB = E .I z (6.16) ecuación que nos dice: “el ángulo θz (AB) que forman entre sí dos secciones de la viga flexionada, es igual al área del diagrama de momentos flectores comprendida entre A y B: ( S M AB ) , dividido por el módulo de rigidez de la viga: E.Iz” Observaciones: 1º.- En las expresiones del primer teorema de Mohr se consideran positivos los ángulos θz que vayan en sentido horario, siempre que la sección A esté situada a la izquierda de la sección B. 2º.- En el caso de una viga en la que conozcamos una sección que no gire (por ejemplo casos de empotramientos), podremos conocer mediante este teorema, de forma directa, el giro de cualquier otra sección de la misma θB A θA=0 B Fig.6.10 ϑ AB = ϑ A − ϑB = (como ϑ A = 0) = −ϑB 8 Sección 6.3: Método de los Teoremas de Mohr Segundo Teorema de Mohr: El segundo teorema de Mohr nos da la distancia en vertical, δBA, que hay desde un punto B de la elástica a la tangente en otro punto A de la elástica. xB dx x xA x B A D C B2 y B0 dθ B1 δ BA θ tag en D tag en C B´ dx x tag en A xB - x B A x Mz Mz Fig.6.11 Para calcular δBA haremos lo siguiente: por dos puntos C y D de la elástica, muy próximos, situados a una distancia: x y x+dx respectivamente, trazamos las tangentes, las cuales interceptan al segmento BB´= δBA en el segmento diferencial B1B2, cuya longitud será: B1 B2 = B1 B0 − B2 B0 = ( xB − x ).tagϑ − ( xB − x ).tag (ϑ − dϑ ) y para el caso de pequeñas deformaciones B1 B2 ≅ ( xB − x ).ϑ − ( xB − x ).(ϑ − dϑ ) = ( xB − x ).d ϑ sumando las longitudes de los segmentos diferenciales B1B2 al mover los puntos C y D desde A hasta B, tendremos la longitud total δBA que queremos calcular. Así: B δ BA = BB´ = ∫ ( x B − x ).dϑ A y si finalmente se sustituye el valor absoluto de dθ obtenido en el primer teorema de Mohr: B M .( x − x ).dx (6.17) δ BA = ∫ z B E . I z A 9 Tema 6: Flexión: Deformaciones Caso particular: En el caso de que el módulo de rigidez de la viga sea constante: E.Iz = cte, la ecuación 6.17. se podrá expresar también de la siguiente manera: B δ BA M .( x − x ).dx =∫ z B = ( E .I z = cte) = E .I z A B ∫M z .( xB − x ).dx A E .I z = QBM AB E .I z (6.18) ecuación que nos dice: “la distancia en vertical: δBA que hay desde un punto B de la elástica a la tangente en otro punto A de la misma, es igual al momento estático respecto del primer punto B del área del diagrama de momentos flectores comprendida entre ambos puntos: Q BM AB , dividido por el módulo de rigidez a flexión de la viga: E.Iz” Observaciones: 1º.- En las expresiones del segundo teorema de Mohr, cuando δBA>0, indicará que el punto B está situado por encima de la tangente en A, independientemente, en este caso, del orden en que estén situados los puntos A y B. 2º.- En el caso de una viga en la que conozcamos una sección que no gire (por ejemplo casos de empotramientos), podremos conocer mediante este teorema, de forma directa, la flecha en un punto cualquiera de la misma. tag en A δBA = yB A x B y Fig.6.12 3º.- Si la flexión de la viga fuera debida a un momento flector My y por tanto la elástica estuviera en el plano xz las expresiones de los teoremas de Mohr: (6.15), (6.16), (6.17) y (6.18), serían las mismas, sin más que cambiar: Mz → M y E.Iz → E.Iy y los giros y flechas obtenidos serían: θz → θ y y → z 4º.- Si la flexión de la viga fuese debida a Mz y My conjuntamente se procedería de forma análoga a lo indicado para los otros dos métodos expuestos. 10