Ejercicios resueltos

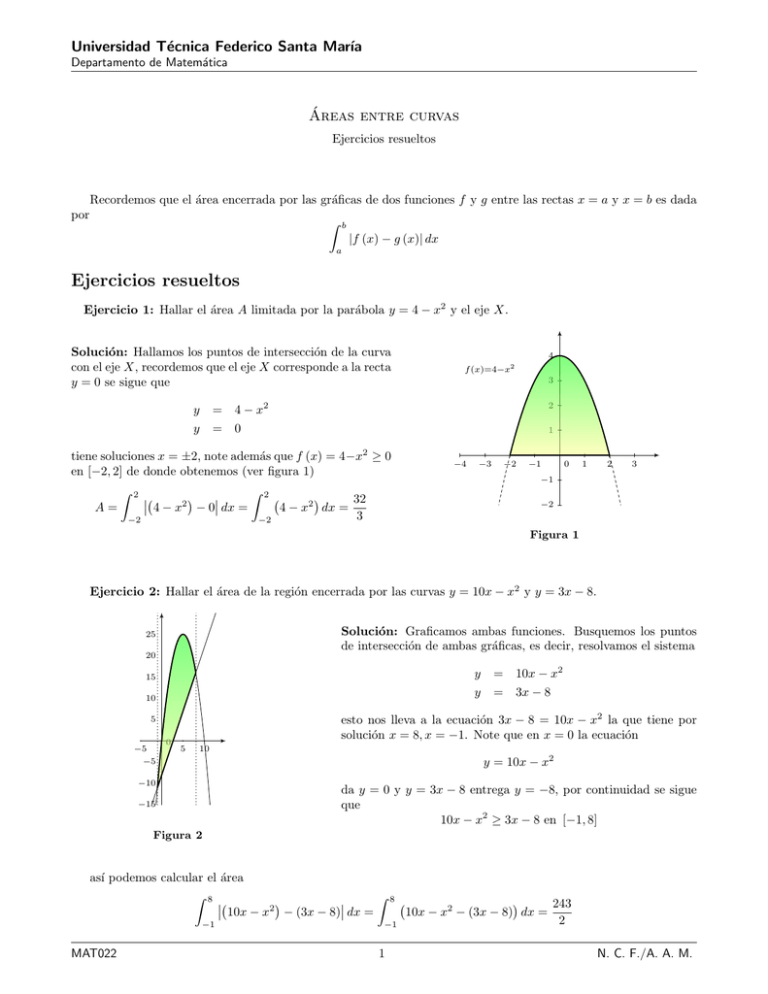
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
Áreas entre curvas
Ejercicios resueltos
Recordemos que el área encerrada por las gráficas de dos funciones f y g entre las rectas x = a y x = b es dada
por
b
Z
|f (x) − g (x)| dx
a
Ejercicios resueltos
Ejercicio 1: Hallar el área A limitada por la parábola y = 4 − x2 y el eje X.
Solución: Hallamos los puntos de intersección de la curva
con el eje X, recordemos que el eje X corresponde a la recta
y = 0 se sigue que
Z
3
y
=
4 − x2
2
y
=
0
1
tiene soluciones x = ±2, note además que f (x) = 4−x2 ≥ 0
en [−2, 2] de donde obtenemos (ver figura 1)
2
4 − x2 − 0 dx =
A=
4
f (x)=4−x2
−2
Z
2
−2
−4
−3
−2
−1
0
1
2
3
−1
32
4 − x2 dx =
3
−2
Figura 1
Ejercicio 2: Hallar el área de la región encerrada por las curvas y = 10x − x2 y y = 3x − 8.
Solución: Graficamos ambas funciones. Busquemos los puntos
de intersección de ambas gráficas, es decir, resolvamos el sistema
25
20
15
y
=
10x − x2
10
y
=
3x − 8
esto nos lleva a la ecuación 3x − 8 = 10x − x2 la que tiene por
solución x = 8, x = −1. Note que en x = 0 la ecuación
5
0
−5
5
10
y = 10x − x2
−5
−10
da y = 0 y y = 3x − 8 entrega y = −8, por continuidad se sigue
que
10x − x2 ≥ 3x − 8 en [−1, 8]
−15
Figura 2
ası́ podemos calcular el área
Z 8
Z
10x − x2 − (3x − 8) dx =
−1
MAT022
8
−1
1
243
10x − x2 − (3x − 8) dx =
2
N. C. F./A. A. M.
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
Ejercicio 3: Hallar el área encerrada por la gráfica de las curva y = x2 − 8x + 10, el eje X, y las rectas x = 2
y x = 5.
Solución: Notemos que x2 − 8x + 10 tiene por gráfica una
parábola, además
√ √ x2 − 8x + 10 = 0 ⇔ x − 4 − 6
x− 4+ 6 =0
0
5
2
x − 8x + 10 − 0 =
2
Z
4
6
−2
se sigue que x2 − 8x + 10 ≤ 0 entre las raı́ces, en particular, en el
intervalo [2, 5] es negativa. El área buscada es entonces
Z
2
−4
−6
5
− x2 − 8x + 10 dx = 15
2
Figura 3
Ejercicio 4: Hallar el área A encerrada por las curvas y = sin x, y = cos x entre las rectas x = 0 y x = π.
1
Solución: Buscamos las intersecciones de las curvas y =
sin x, y = cos x en el intervalo [0, π], esto nos lleva a buscar
las soluciones de sin x = cos x, ası́ x = π/4. En 0, π4
cos x ≥ sin x y en π4 , π se cumple sin x ≥ cos x ası́
0.5
−0.5
0.5
1
1.5
2
2.5
3
Z
π
−0.5
π/4
Z
|sin x − cos x| dx
0
(cos x − sin x) dx
=
0
0
Z
π
(sin x − cos x) dx
+
−1
=
−1.5
√
π/4
√
√
2−1 +
2+1 =2 2
Figura 4
Ejercicio 5: Hallar el área encerrada entre las curvas 8y = x3 y
8y = 2x3 + x2 − 2x
Solución: Buscamos los puntos de intersección de las curvas, es decir, resolvemos el sistema
8y
=
x3
8y
=
2x3 + x2 − 2x
0.5
−2.5
2x3 + x2 − 2x = x3
−2
−1.5
−1
−0.5
0.5
1
0
entonces
−0.5
⇔
x3 + x2 − 2x = 0
−1
⇔ x (x − 1) (x + 2) = 0
−1.5
se sigue que las curvas intersectan en x = 0, x = 1, x = −2,
además de forma analı́tica podemos determinar cual de las
curvas se encuentra arriba y en que intervalo
MAT022
2
Figura 5
N. C. F./A. A. M.
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
En efecto
2x3 + x2 − 2x ≥ x3 ⇔ x (x − 1) (x + 2) ≥ 0
luego utilizando la tabla
x
x−1
x+2
x (x − 1) (x + 2)
−
−
−
−
−
−
−
−
−2
−
−
0
0
−
−
+
+
−
−
+
+
0
0
−
+
0
+
−
+
−
1
+
0
+
0
+
−
+
−
+
+
+
+
+
+
+
+
obtenemos que en el intervalo [−2, 1] se cumple
2x3 + x2 − 2x
x3
≥
8
8
si y solo si x ∈ [−2, 0], ası́
Z 1 3
2
x3 2x + x − 2x
− dx
8
8
−2 Z
0
=
−2
Z
+
0
1
!
2x3 + x2 − 2x
x3
−
dx
8
8
!
2x3 + x2 − 2x
x3
−
dx
8
8
1
5
37
+
=
3 96
96
=
Ejercicio 6: Encontrar el área encerrada por las curvas y 2 = x y y = 3x − 10.
Solución: Buscamos las intersecciones de las curvas, es
decir, resolvemos el sistema
y2
= x
y
=
3x − 10
2
en este caso es más conveniente resolver para y, se sigue de
estas ecuaciones que
1
y + 10
y =
3
2
que tiene soluciones y = 2, y = − 53 , valores que corresponden a x = 4 y x = 25
9 respectivamente. Los gráfico de
estas curvas corresponden a una parábola y una recta pero
la parábola tiene directriz perpendicular al eje X, es más
conveniente mirar el problema como si el eje Y fuera el eje
X, nos queda
Z 2 2
y + 10 A =
y −
dy
3
−5/3
Z 2 y + 10
1331
=
− y 2 dy =
3
162
−5/3
−1
0
1
2
3
4
−1
−2
Figura 6
El problema también puede ser visto desde el eje X, la parábola y 2 = x entrega dos funciones
√
y =
x
√
y = − x
MAT022
3
N. C. F./A. A. M.
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
se sigue que podemos calcular el área como
Z 25/9
Z
√
√ x − − x dx +
0
4
√
x − (3x − 10) dx
25/9
(vea la figura 6) ası́
500 331
1331
+
=
81
162
162
Ejercicio 7: Hallar el área encerrada por el eje X y las curvas y = arcsin x, y = arccos x.
Solución: Notemos que y = arcsin x, y = arccos x están
definidas para x ∈ [−1, 1] además
h π πi
y = arcsin x ⇔ sin y = x con y ∈ − ,
2 2
y = arccos x ⇔ cos y = x con y ∈ [0, π]
1
0.5
estas curvas intersectan en y = π4 , podemos mirar el problema de una manera más conveniente desde el eje Y , en
tal caso el área queda
Z
π/4
(cos y − sin y) dy =
√
−0.5
0.5
1
0
2−1
−0.5
0
Figura 7
mirando el problema desde el eje X el cálculo del área es
Z 1/√2
Z
arcsin x dx +
√
1/ 2
0
=
=
√
1
arccos x dx
√
1√
1
1√
1
π−
2π +
2−1 +− 2
8
2
8
2
2−1
Ejercicio 8: Considere los puntos A = (−2, 4) y B = (1, 1) sobre la parábola y = x2 y los puntos C = (1, s)
y D = (−2, r) tales que el segmento CD es tangente a la parábola y paralelo a AB. Hallar el área encerrada por
los segmentos AD, DC, CB y la parábola.
Solución: Basta encontrar la recta que contiene el segmento CD, la ecuación tendrá la forma
y = mx + n
note que al ser paralela a la recta que contiene AB debe tener pendiente
4−1
= −1
−2 − 1
0
esto nos permite además encontrar el punto de tangencia x2 = 2x se sigue
m=
2x = −1 =⇒ x = −
MAT022
4
1
2
N. C. F./A. A. M.
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
4
al estar sobre
la parábola se tiene que el punto de tangencia
es − 21 , 41 y como el punto esta sobre la recta se sigue:
1
1
1
= −1 −
+ n =⇒ n = −
4
2
4
3
2
se sigue que la recta es
1
y = −x −
1
4
−2
−1
de donde obtenemos finalmente que el área buscada es
Z 1
1
9
x2 − −x −
dx =
4
4
−2
1
0
−1
−2
Figura 8
Ejercicio 9: Hallar el área encerrada por las curvas
√
xy
√
x+ y
=
9
=
4
√
√
Solución: Como consideramos la curva x√+ y = 4,
√
estamos asumiendo x ≥ 0, y ≥ 0. De la curva x + y = 4
obtenemos
√ 2
y = 4− x
10
8
busquemos el punto de intersección de las curvas
6
√
√ 2
y
√
x + y + 2 xy
4
x+
=
16
=
16
de la primera obtenemos
2
x + y + 6 = 16
0
2
4
6
8
se sigue
10
x + y = 10
Figura 9
luego tenemos el sistema
xy
=
9
x+y
=
10
multiplicando la segunda por x se sigue
x2 + xy = 10x y xy = 9
entonces
x2 − 10x + 9 = 0 =⇒ x = 1 ∨ x = 9
MAT022
5
N. C. F./A. A. M.
Universidad Técnica Federico Santa Marı́a
Departamento de Matemática
los puntos de intersección son (1, 9) y (9, 1). Se sigue que el área es
Z 9
√ 2 9
88
4− x −
dx =
− 18 ln 3
x
3
1
Ejercicio 10: Hallar el área encerrada por la astroide
x2/3 + y 2/3 = 1
Solución: Por la alta simetrı́a del problema(simetrı́a respecto al eje Y , al eje X y al origen) basta calcular el área
encerrada en el primer cuadrante, note que
1
0.5
y 2/3 = 1 − x2/3
−1
−0.5
0.5
se sigue
1
3/2
y = 1 − x2/3
0
−0.5
y x ∈ [0, 1] entonces (sustitución trigonométrica x = sin3 t)
−1
Z
A=4
0
Figura 10
1
3/2
3
1 − x2/3
dx = π
8
Ejercicio 11: Encontrar el área encerrada por la curva cerrada y 2 = x2 − x4 .
1
Solución: Note que y 2 ≥ 0 entonces x2 − x4 ≥ 0 ⇔
x2 1 − x2 ≥ 0 esto es x ∈ [−1, 1]. De la ecuación
0.5
y 2 = x2 − x4
−1
−0.5
obtenemos las funciones
p
p
y = ± x2 − x4 = ± |x| 1 − x2
0.5
1
−0.5
−1
Figura 11
se sigue que el área esta dada por
Z
1
p
1 − x2 − − |x| 1 − x2 dx
|x|
p
|x|
p
−1
Z
=
1
2
−1
Z 1
=
x
4
p
1 − x2 dx
1 − x2 =
0
MAT022
6
4
3
N. C. F./A. A. M.