Solución oficial por el alumno Rodolfo F. Gamarra

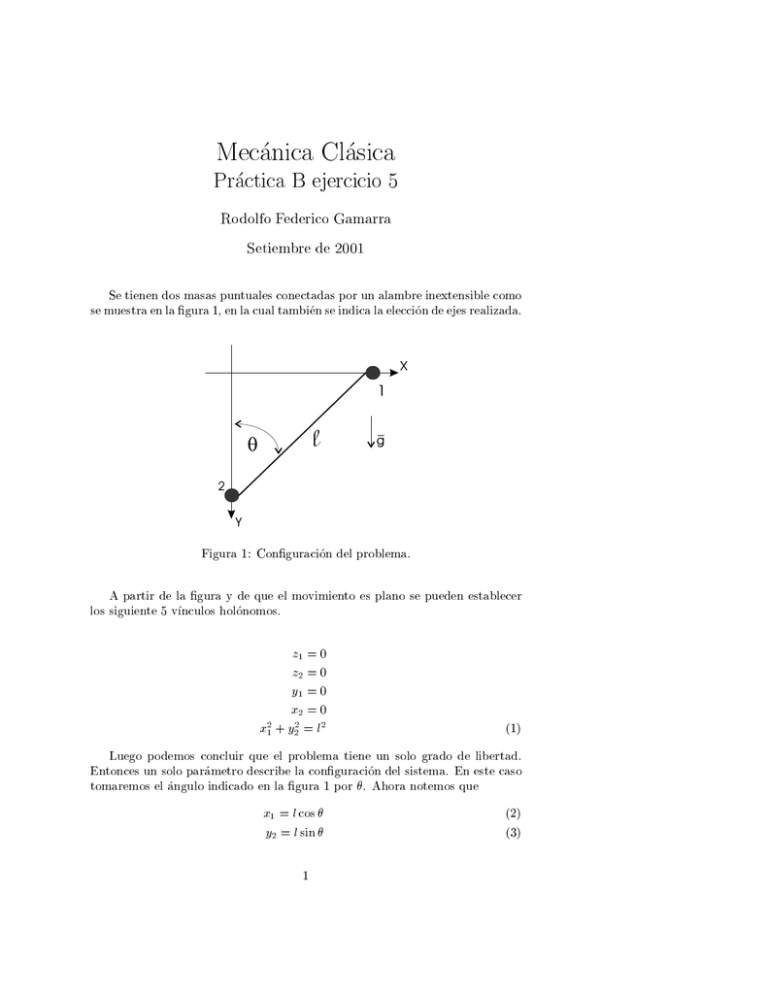
Mecanica Cl
asica
Pr
actica B ejercicio 5
Rodolfo Federico Gamarra
Setiembre de 2001
Se tienen dos masas puntuales conectadas por un alambre inextensible como
se muestra en la gura 1, en la cual tambien se indica la eleccion de ejes realizada.
Figura 1: Conguracion del problema.
A partir de la gura y de que el movimiento es plano se pueden establecer
los siguiente 5 vnculos holonomos.
=0
=0
y1 = 0
x2 = 0
2
x1 + y22 = l2
z1
z2
(1)
Luego podemos concluir que el problema tiene un solo grado de libertad.
Entonces un solo parametro describe la conguracion del sistema. En este caso
tomaremos el angulo indicado en la gura 1 por . Ahora notemos que
= l cos y2 = l sin x1
1
(2)
(3)
Por otro lado, las fuerzas (que no son de vnculo) en este problema son los
pesos respectivos a cada masa. Pero en el caso de la masa 1 los desplazamientos
compatibles con el vnculo impuesto son perpendiculares a la fuerza, por lo que
esta no realiza trabajo alguno. Entonces recordando el principio de D'Alambert
XF
(
i
i
p_ ) Ær
i
i
=0
(4)
y aplicandolo para el caso que nos ocupa
(m2 g
m2 y2 )Æy2
m1 x
1 Æx1
=0
(5)
Ahora bien, nos queda por relacionar x1 y y2 y los desplazamientos virtuales
con la coordenada . Esto lo podemos conseguir a partir de 2 y 3. En primer
lugar podemos escribir
= l sin Æ
Æx1 = l cos lÆ
(6)
(7)
Æy2
y para el caso de las primeras derivadas, analogamente
= l sin _
x_ 1 = l cos _
y_ 2
(8)
(9)
A partir de lo cual podemos calcular las aceleraciones
= l sin x
1 = l cos l_2 cos y2
Æ
(10)
(11)
l_2 sin Entonces reemplazando en 5 la ecuaciones 6, 7, 10 y 11, agrupando y ya que
es arbitrario1 , se tiene
(m2 sin2 + m1 cos2 )+
_2 sin cos (m2 m1 )+
g
m2 sin = 0
l
(12)
Ahora bien, en la ecuacion anterior podemos analizar el caso de peque~nas
oscilaciones (; _ 1).Entonces tomando sin y cos 1 la ecuacion 12
queda.
(m2 2
+ m1 ) + _2 (m2
g
m1 ) + m2 l
=0
(13)
Lo que puede simplicarse descartando los terminos de orden superior (estamos en el caso de peque~nas oscilaciones).
1 Al ser arbitrario se tiene que anular el factor que lo multiplica, por eso Æ no aparece en
la ecuacion 12.
2
 +
m2 g
m1 l
=0
(14)
Vemos que 14 no es otra cosa que la ecuacion de un pendulo plano (para
peque~nas oscilaciones) con una longitud igual a la de la barra (la que serva de
1
vnculo) multiplicada por m1 =m2 (o sea leq = lm
m2 ) . Entonces podemos ver que
el perodo para las oscilaciones ( ) resulta.
=
q
2
m2 g
m1 l
(15)
Para lo cual podemos analizar dos casos lmites.
= 1 mlim = 0
mlim
m21 !0
m21 !1
3
(16)