Document

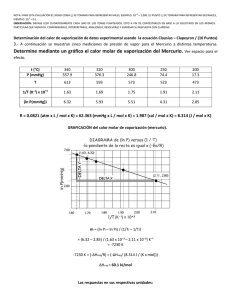
Cinética Química
Problemas
1.1. La pirólisis del dimetil mercurio resultó ser una reacción de primer orden. Varias
muestras del sustrato se mantuvieron a temperatura constante durante un periodo de
tiempo conocido, y después se determinó el grado de descomposición de cada una
de ellas. A partir de los datos que se muestran a continuación, deduzca la constante
de velocidad de la descomposición a cada temperatura y calcule los parámetros de
Arrhenius, Ea y A.
T [°C]
t [min]
331.7
319.8
305.2
% de descomposición [%]
120
32.4
330
35.3
840
33.5
Si se trata de una ecuación de primer orden,
R  k[dimetil mercurio] 
d[dimetil mercurio]
dt
pero [dimetil mercurio] = [dimetil mercurio]0 – x
dx
 k ([dimetil mercurio]0  x)
dt

 dx
 k  dt
[dimetil mercurio]0  x
 ln([dimetil mercurio]0  x)  kt  C
con t = 0, x = 0 => C = – ln([dimetil mercurio]0)
 ln([dimetil mercurio]0  x)  kt  ln([dimetil mercurio]0 )
 [dimetil mercurio]0  x 
   kt
ln
[
dimetil
mercurio
]
0


...(1)
[dimetil mercurio]0  x
es el porcentaje de dimetil mercurio sin descomponer,
[dimetil mercurio]0
por tanto, el porcentaje del dimetil mercurio que se descompone, es
[dimetil mercurio]0  x
1
y la ecuación (1) queda:
[dimetil mercurio]0
pero
 % de descomposición 
ln1 
  kt
100


...(2)
Cinética Química
despejamos k de la ecuación (2):
 % de descomposición 
ln1 

100


k 
t
t [s]
7200
19800
50400
 % de descomposición 
 ln1 

100


-0.391562203
-0.435408984
-0.407968238
–1
k [s ]
5.43836E-05
2.19904E-05
8.09461E-06
Ahora, con la ecuación de Arrhenius:
ln k  ln A 
Ea 1
R T
hacemos la gráfica de ln k Vs 1/T:
Ecuación de Arrhenius
ln k
-9.819447198
-10.72490671
-11.72431241
ln k
–1
1/T [K ]
0.0016533
0.00168648
0.00172906
-9.5
0.00164
-10
0.00166
0.00168
0.0017
0.00172
-10.5
-11
-11.5
y = -25068x + 31.599
R2 = 0.9982
-12
1/T
de donde se desprende que la pendiente
 25068 K  
Ea
R
J 

Ea  (25068 K ) R  (25068 K ) 8.314
 =>
mol K 

y la ordenada al origen
31.599  ln A
A  e 31.599  5.28  1013 s -1
Ea  2.08  10 5
J
mol
0.00174
Cinética Química
1.2. La concentración de radicales bencilo, R∙, disminuye como se muestra a
continuación, a partir del pulso de electrones que origina la formación de estos
radicales. Determine el orden de la descomposición y su constante de velocidad.
5
–3
[R∙] [×10 mol dm ]
7.14
6.53
5.38
4.55
3.82
3.45
2.8
1.97
1.55
1.26
1.15
t [s]
31
43
60
80
101
121
150
220
280
350
400
Para determinar el orden de la reacción, graficamos [R∙], ln [R∙] y 1/ [R∙] Vs t:
t [s]
31
43
60
80
101
121
150
220
280
350
400
t [s]
31
43
60
80
101
121
150
220
280
350
400
5
Reacción de orden cero
–3
[R∙] [×10 mol dm ]
7.14
6.53
5.38
4.55
3.82
3.45
2.8
1.97
1.55
1.26
1.15
8
7
6
5
4
3
2
1
0
[R∙] [×105 mol
dm–3]
0
100
300
400
500
t [s]
Reacción de primer orden
–3
ln ([R∙]) [dm mol]
-9.547212689
-9.636518522
-9.830237091
-9.997798232
-10.17267504
-10.27455123
-10.48330605
-10.83489192
-11.07467053
-11.28181374
-11.37316352
200
-9.5
0
100
200
Lineal (ln ([R∙]))
-10
-10.5
-11
300
ln
([R∙])
y = -0.005x - 9.5769
R2 = 0.9575
-11.5
t [s]
400
Cinética Química
Reacción de segundo orden
t [s]
31
43
60
80
101
121
150
220
280
350
400
3
–1
1/[R∙] [dm mol ]
0.14005602
0.15313936
0.18587361
0.21978022
0.2617801
0.28985507
0.35714286
0.50761421
0.64516129
0.79365079
0.86956522
100000
90000
1/[R∙]
80000
Lineal (1/[R∙])
70000
60000
50000
40000
30000
y = 205.1x + 5981.7
2
R = 0.9981
20000
10000
0
0
100
200
300
400
t [s]
Podemos observar [R∙] es una curva, por lo que la reacción no puede ser de orden
cero. En la gráfica vemos también que el coeficiente de correlación de 1 / [R∙] es
más cercano a 1 que el de ln [R∙], por tanto, la reacción es de segundo orden , con
una constante de rapidez 2k = 205.1 dm3 mol–1 s–1 ≈ 2.05 × 108 dm3 mol–1 s–1 .
1.3. En disolución acuosa acidulada, el CeIV reacciona con H2O2 para dar CeIII y O2. En
un experimento con concentraciones iniciales [CeIV] = 9.25 × 10–5 mol dm–3 y
[H2O2] = 7.5 × 10–6 mol dm–3, se encontró que la concentración inicial de peróxido
de hidrógeno disminuía con el tiempo como se muestra a continuación:
6
t [ms]
2
4
6
8
10
12
14
16
18
20
–3
[H2O2] [×10 mol dm ]
6.23
4.84
3.76
3.2
2.6
2.16
1.85
1.49
1.27
1.01
Demuestre que la reacción sigue una cinética de pseudo-primer orden y calcule la
constante de velocidad.
Si consideramos que [CeIV] >> [H2O2], esto es, que la [CeIV] se mantiene constante
durante la reacción, la ecuación de rapidez queda expresada como:

d[H 2 O 2 ]
 k ps [H 2 O 2 ]
dt
Si [H 2 O 2 ]  [H 2 O 2 ]0  x y hacemos las operaciones algebraicas necesarias,
tenemos:
Cinética Química
 ln [H 2 O 2 ]0  x   ln [H 2 O 2 ]0   k ps t
 ln [H 2 O 2 ]  ln [H 2 O 2 ]0   k ps t
Al graficar el – ln [H 2 O 2 ] contra t, observamos que efectivamente, el coeficiente
de correlación es prácticamente uno. Es decir, la ecuación ajustada a los datos es
prácticamente lineal. La constante de rapidez es
k ps  98.782  k[Ce IV ]
Por lo que
t [s]
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0.02
– ln ([H2O2])
11.800608
11.986134
12.238596
12.491092
12.65236
12.859999
13.045402
13.200325
13.416734
13.576494
13.80556
k ps
IV
[Ce ]

98.782
9.25  10 5
=>
k  1.07  10 6
Ecuación de pseudo-primer orden
14
13.5
ln ([H2O2])
k
13
12.5
y = 98.782x + 11.837
R2 = 0.9973
12
11.5
0
0.005
0.01
0.015
0.02
t [s]
2.2. La reacción del radical 1,1-difenil-2-picrilhidracilo (DFPH) con el ión hierro (II) en
una disolución de agua/etanol se estudio espectrométricamente. En un experimento
a 293 K se encontró que la absorbancia A (debida al DFPH) disminuía con el
tiempo como se describe a continuación:
t [s]
0
17
37
55
76
94
114
138
157
178
204
∞
A
0.54
0.49
0.44
0.4
0.36
0.33
0.3
0.27
0.25
0.23
0.21
0.11
Cinética Química
Sabiendo que a t = 0 las concentraciones de los reactivos eran [DFPH] = 1.14 ×10–5
mol dm–3 y [Fe2+] = 2.75 ×10–4 mol dm–3, calcule la constante de velocidad de
segundo orden de esta reacción.
I) Si suponemos que el radical DFPH absorbe energía de acuerdo con la ley de
Lambert-Beer, y la ecuación para obtener la concentración en función de la
absorbancia es:
[DFPH] 
1
A
l
Con los datos de concentración y absorbancia a t = 0 tenemos que
1 [DFPH] 1.14  10 5


 2.11 10 5
l
A
0.54
Por tanto
[DFPH]  2.11 10 5 A mol dm 3
…(3)
1) Si suponemos que la [Fe2+] >> [DFPH], y que la ecuación de rapidez es de
segundo orden con respecto al DFPH y de orden cero con respecto al Fe2+, ésta
queda expresada como:
dx
 k dt
[DFPH]0  x 2 ps
donde
k ps  k[Fe 2 ]
que integrada queda
1
1

 k ps t
[DFPH]0  x [DFPH]0
O lo que es lo mismo,
1
1

 k ps t
[DFPH] [DFPH]0
Al graficar [DFPH]–1 Vs. t, utilizando la ecuación (3),
Cinética Química
–1
–1
Ecuación de segundo orden con respecto al DFPH
3
([DFPH]) [mol dm ]
87765.49061
96721.15292
107712.193
118483.4123
131648.2359
143616.2574
157977.8831
175530.9812
189573.4597
206058.1084
225682.6901
250000
200000
1/[DFPH]
t [s]
0
17
37
55
76
94
114
138
157
178
204
150000
y = 680.56x + 82961
R2 = 0.9962
100000
50000
0
0
50
100
150
200
250
t [s]
obtenemos
k ps  680.56 mol -1 dm 3 s -1  k[Fe 2 ]
Por lo que
k
k ps
2
[Fe ]

680.56 mol -1dm 3s -1
2.75  10 4 mol dm -3
=>
k  2.47  10 6 mol-2 dm 6 s -1
b) Si la ecuación de rapidez es de primer orden para ambos reactivos, la expresión
matemática es:
dx
 kdt
[DFPH]0  x  [Fe 2 ]0  x


que integrada queda
[DFPH]0

 ln [DFPH]  ln 
[Fe 2 ]0  [DFPH]0   k [Fe 2 ]0  [DFPH]0 t
2
 [Fe ]0


Al graficar –ln([DFPH]) Vs. t, tenemos



Cinética Química
Ecuación de primer orden con respecto a ambos
reactivos
–3
0
17
37
55
76
94
114
138
157
178
204
–Ln([DFPH]) [mol dm ]
11.3824237
11.4795874
11.5872181
11.6825282
11.7878888
11.8749001
11.9702103
12.0755708
12.1525319
12.2359135
12.3268853
12.6
12.4
-Ln([DPFH])
t [s]
12.2
12
11.8
y = 0.0047x + 11.415
R2 = 0.9952
11.6
11.4
11.2
0
50
100
150
200
t [s]
de donde


k [Fe 2 ]0  [DFPH]0  0.0047 mol dm -3 s -1
por tanto,
k
0.0047
0.0047

[Fe ]0  [DFPH]0 2.75 10  4  1.14  10 5
2
II) Si utilizamos la relación
1  A0  At

a  At  A

  k ps t

pero
a  [DFPH]0
Graficamos:
=>
k  17.5 s -1
250
Cinética Química
Segundo orden
t [s]
17
37
55
76
94
114
138
157
178
204
1/[DFPH]0 * [ (A0 - At) / (At - A∞) ]
–1
3
[mol dm ]
11542.01293
26581.60553
42347.24743
63157.89474
83732.05742
110803.3241
148026.3158
181704.2607
226608.1871
289473.6842
350000
300000
250000
200000
y = 1450.5x - 36809
R2 = 0.9657
150000
100000
50000
0
-50000 0
50
100
150
200
t [s]
De donde
k ps  1450.5 mol -1 dm 3 s -1  k[Fe 2 ]
Por lo que
k
k ps
2
[Fe ]

1450.5 mol -1dm 3s -1
2.75  10 4 mol dm -3
=>
k  5.27  10 6 mol -2 dm 6 s -1
2.5. La hidrólisis alcalina del carbonato de etileno,
O
OH
O
+
2OH
+
O
2CO3
OH
se siguió por medidas de conductimetría. En un experimento a 298 K, con
concentraciones iniciales [OH–]0 = 0.00514 mol dm–3 y
[ester]0 = 0.00081 mol dm–3, se encontró que la corriente del oscilador I (una
medida de la conductividad específica de la disolución) variaba con el tiempo como
sigue:
t [s]
0
7.5
15
22.5
30
37.5
45
60
67.5
I
80.6
77.7
75
72.3
70
67.5
65.5
62
60.5
250
Cinética Química
75
59
90 56.5
∞ 37.6
Calcule la constante de velocidad para la reacción del primer ión hidróxido con el
éster, suponiendo que a continuación tiene lugar rápidamente la reacción del
segundo OH–.
Utilizamos la relación
1  I0  It

[OH - ]0  I t  I 
t [s]
7.5
15
22.5
30
37.5
45
60
67.5
75
90
Ln [ (I0 - I∞) / (It - I∞) ]
0.069823781
0.139529411
0.214460429
0.283041693
0.363341635
0.432573427
0.566616983
0.630063205
0.697809194
0.822038194

  k ps t

Primer orden
1
0.8
y = 0.0092x + 0.0086
R2 = 0.999
0.6
0.4
0.2
0
0
20
40
60
t [s]
80
100