TRATAMIENTO DE DATOS CON GSLIB

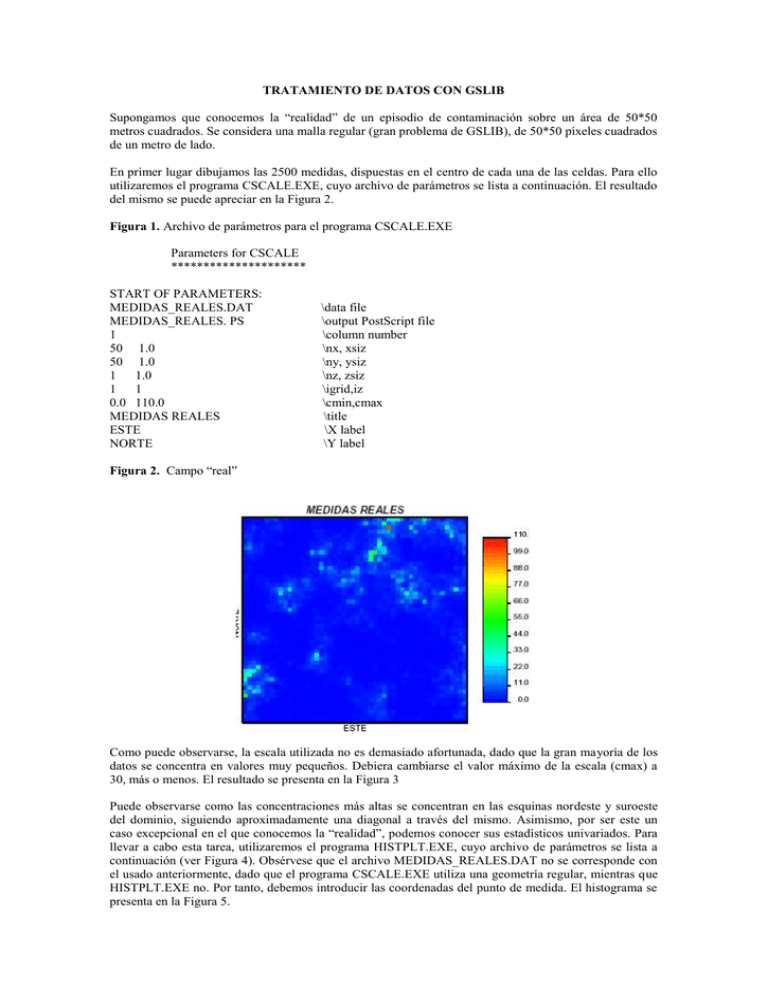
TRATAMIENTO DE DATOS CON GSLIB
Supongamos que conocemos la “realidad” de un episodio de contaminación sobre un área de 50*50
metros cuadrados. Se considera una malla regular (gran problema de GSLIB), de 50*50 píxeles cuadrados
de un metro de lado.
En primer lugar dibujamos las 2500 medidas, dispuestas en el centro de cada una de las celdas. Para ello
utilizaremos el programa CSCALE.EXE, cuyo archivo de parámetros se lista a continuación. El resultado
del mismo se puede apreciar en la Figura 2.
Figura 1. Archivo de parámetros para el programa CSCALE.EXE
Parameters for CSCALE
*********************
START OF PARAMETERS:
MEDIDAS_REALES.DAT
MEDIDAS_REALES. PS
1
50 1.0
50 1.0
1
1.0
1
1
0.0 110.0
MEDIDAS REALES
ESTE
NORTE
\data file
\output PostScript file
\column number
\nx, xsiz
\ny, ysiz
\nz, zsiz
\igrid,iz
\cmin,cmax
\title
\X label
\Y label
Figura 2. Campo “real”
Como puede observarse, la escala utilizada no es demasiado afortunada, dado que la gran mayoría de los
datos se concentra en valores muy pequeños. Debiera cambiarse el valor máximo de la escala (cmax) a
30, más o menos. El resultado se presenta en la Figura 3
Puede observarse como las concentraciones más altas se concentran en las esquinas nordeste y suroeste
del dominio, siguiendo aproximadamente una diagonal a través del mismo. Asimismo, por ser este un
caso excepcional en el que conocemos la “realidad”, podemos conocer sus estadísticos univariados. Para
llevar a cabo esta tarea, utilizaremos el programa HISTPLT.EXE, cuyo archivo de parámetros se lista a
continuación (ver Figura 4). Obsérvese que el archivo MEDIDAS_REALES.DAT no se corresponde con
el usado anteriormente, dado que el programa CSCALE.EXE utiliza una geometría regular, mientras que
HISTPLT.EXE no. Por tanto, debemos introducir las coordenadas del punto de medida. El histograma se
presenta en la Figura 5.
Figura 3. Campo real, sin considerar los valores extremadamente altos.
Figura 4. Archivo de parámetros para el programa HISTPLT.EXE
Parameters for HISTPLT
**********************
START OF PARAMETERS:
MEDIDAS_REALES.DAT
3 0
HISTOGRAMA_REAL.PS
-0.99 999999.
0.0
110.0
55
0
HISTOGRAMA Y ESTAD. REALES
\data file
\column for variable and weight
\output PostScript file
\trimming limits
\histogram minimum and maximum
\number of classes
\1=log scale, 0=arithmetic
\title
Figura 5. Histograma de las medidas del campo “real”
De nuevo hemos cometido el mismo error, dado que el límite superior del histograma se corresponde con
el máximo en los datos. Si lo dibujamos cambiando ese límite superior a 20 (la frecuencia de muestras es
inapreciable a partir de este valor), se obtiene el histograma de la Figura 6.
Figura 6. Histograma de las medidas del campo “real”, reduciendo su límite máximo
Obsérvese que en la figura anterior aparecen los estadísticos univariados de la variable. Estos no
dependen del máximo escogido para el dibujo del histograma, ni del número de clases utilizadas. En este
caso, se confirma lo antes dicho. Los datos “reales” se acomodan entorno a valores muy bajos, con una
desviación bastante baja. Esto quiere decir que el campo es bastante uniforme, como se observó en los
dibujos del campo (de hecho, en el 75% de los puntos - cuartil superior -, la concentración es menor que
2.56. No obstante, hay una serie de valores extremos que, al estudiar un episodio de contaminación, por
ejemplo, son los de mayor interés, con valores mayores que 100.
Una vez obtenida una visión global del campo “real”, pongamos a prueba nuestros conocimientos.
Imaginemos que ahora no conocemos el campo real, sino que disponemos de 97 puntos muestreados. De
esos 97, se seleccionan los de mayor concentración y se obtienen 43 muestras adicionales entorno a ellos.
Finalmente se cuenta con un total de 140 medidas. Para dibujar su posición y su valor, utilizaremos el
programa SCATPLT.EXE, cuyo archivo de parámetros se muestra en la Figura 7.
Figura 7. Archivo de parámetros para el programa SCATPLT.EXE
Parameters for SCATPLT
**********************
START OF PARAMETERS:
MEDIDAS.DAT
1 2 3
MEDIDAS.PS
-1.0 1.0e21
-1.0 1.0e21
0.0 50.0
0.0 50.0
Medidas de dos campañas
\data file
\column for X, Y, and weight
\output Postscript file
\min and max variable X
\min and max variable Y
\xmin and xmax
\ymin and ymax
\title
El resultado de este programa se presenta en la Figura 8. Obsérvese la agrupación entorno a ciertos puntos
(como cruces). No obstante, este gráfico no ofrece ninguna información sobre los valores de las medidas.
Ciertamente, resulta más cómodo el uso de otros programas, tipo Grapher o Surfer. El resultado del uso
de Surfer se presenta en la Figura 9..
Figura 8. Disposición y estadísticos de las medidas de las dos campañas
Figura 9. Marcados con círculo los datos del primer muestreo y con cruz los del segundo. Tamaños de
símbolo proporcionales al valor de la concentración medida. Realizada con la herramienta POSTMAP de
SURFER.
45
40
35
30
25
20
15
10
5
5
10
15
20
25
30
35
40
45
No obstante, no se observan los valores de las medidas. En cambio, utilizando la herramienta CLASSED
POST MAP de Surfer se obtiene el siguiente resultado (ver Figura 10). En el se observan los símbolos,
con tamaño proporcional al valor de la medida, así como el valor de la misma.
Figura 10. Detalle de las medidas con sus valores asociados. Realizada con la herramienta CLASSED
POST MAP de Surfer.
0.34
1.96
0.4
0.81
0.83
45
15.77
5.54
7.53
10.2
5.05 5.38
0.51
2.33
40
0.67
1.78
1.1
2.84
1.82
0.65
3.56
9.01
8.03
2.52
9.27
0.11
4.89
3.04
0.79
0.84
1.38
2.34
0.33
0.17
1.01
20
2.74
10.27
3.61
15 5.54
8.71
2.55
15.77
7.56
6.26
7.92
10
6.49
20.35
8.9
12.74
0.45
1.27
0.09
1.34
0.34
0.99
0.28
5
0.09
10
15
0.94
0.93
0.62
1.66
0.96
0.92
0.19
0.19 0.1
3.33 0.06
1.21
0.06
0.22
1.7
5
0.11 0.1
2.17
2.97
19.44
9.08
4.92
2.96
2.99
0.280.26
3.81
2.13
1.38
0.16
1.11
0.71
0.24
0.57
1.02
3.35
3.51
9.08
3.64
5.31
2.22
3.59
2.82
9.42
18.76
5.26 2.28
1.988.48 18.64
8.34
2.51
7.94
1.21
0.46
2.75
0.18 1.37
3.21
4.29
6.41
7.71
2.33
1.71
30
0.16
25
1.36
4.6
2.7621.08
58.32
17.19
22.75
11.08
0.99
0.34
0.32
35
5.15
2.47
0.19
0.08
1.81
1.89
0.89
20
25
0.06
0.45
1.37
2.96
7.56
to
to
to
to
to
0.31
30
35
40
45
0.45
1.37
2.96
7.56
58.33
EL hecho de usar un sistema de información geográfica nos permita asimismo, dibujar mapas en color de
nuestros datos, que ayudan sobremanera a la comprensión de los mismos (ver Figura 11)
Figura 11. Mapeado a color de las medidas. Realizada con la herramienta CONTOUR PLOT de Surfer.
Pese a que en ningún caso vamos a conocer la realidad del campo (si en éste), pueden compararse los dos
mapas presentados en las Figuras 11 y 3. Así, puede verse que las medidas reproducen aproximadamente
la forma de la “pluma” de contaminación.
Conozcamos ahora los estadísticos univariados de nuestras medidas. Para ello, volvemos a aplicar el
programa HISTPLT, con el que obtenemos el histograma de nuestros datos. El archivo de datos se
muestra en la Figura 12. Naturalmente, ahora se fijado el límite superior del histograma a 20, por lo que
se comentó anteriormente. El resultado (histograma y estadísticos) se muestra en la Figura 12.
Figura 12. Archivo de parámetros para el programa HISTPLT.EXE
Parameters for HISTPLT
**********************
START OF PARAMETERS:
MEDIDAS.DAT
3 0
HISTOGRAMA_MEDIDAS.PS
-0.99 999999.
0.0 20.0
40
0
HISTOGRAMA DE MEDIDAS
\data file
\column for variable and weight
\output PostScript file
\trimming limits
\histogram minimum and maximum
\number of classes
\1=log scale, 0=arithmetic
\title
Figura 13. Histograma y estadísticos de las medidas
Como se puede observar, el hecho de considerar medidas adicionales alrededor de las de mayor
concentración, añade “ruido” a nuestros resultados. Comparemos los estadísticos (ver Tabla 1). Así, la
media es 4.35, cuando la “real” era de 2.58. Lo mismo ocurre con la desviación estándar, que es 6.7,
cuando la real era 5.15. El mínimo prácticamente no varía (hay tantos puntos con baja concentración que
es muy fácil muestrear uno de ellos). En general, ningún cuartil varía ostensiblemente, salvo el máximo,
que cae “en picado”, debido a que, dada la poca densidad de puntos con muy alta concentración, resulta
difícil muestrear en uno de ellos.
Tabla 1. Comparación de los estadísticos “reales” y los de las medidas
Reales
Medidas
n
2500
140
Media
2.58
4.35
Desv. St.
5.15
6.7
Mínimo
0.01
0.06
Q. 25
0.34
0.69
Q. 50
0.96
2.12
Q. 75
2.56
5.35
Máximo
102.7
58.32
Así, resulta conveniente realizar una desagrupación de los datos. Para ello puede procederse de dos
formas distintas: 1) Rápidamente (pero muy poco elegante), considerando únicamente las 97 muestras de
la primera campaña.
2) Usando el algoritmo de desagrupación (“declustering”) de GSLIB. Este algoritmo
calculará un peso asociado a cada medida, en función de su proximidad a las demás. Así no se
desaprovechan datos que, ciertamente, aportan información pero no demasiada. En zonas donde los datos
estén muy agrupados (las de la segunda campaña) recibirán menor peso que zonas con poca densidad de
datos.
-
Posibilidad 1. Considerar únicamente los datos de la primera campaña
Procedemos de igual modo, calculando el histograma y los estadísticos. Los resultados se presentan en la
Figura 14 y en la Tabla 2.
Figura 14. Histograma y estadísticos de los datos de la primera campaña
Tabla 2. Comparación de los estadísticos “reales” y los de las medidas totales y sólo las de la primera
campaña.
Reales
Medidas
M. 1C
n
2500
140
97
Media
2.58
4.35
2.21
Desv. St.
5.15
6.7
3.17
Mínimo
0.01
0.06
0.06
Q. 25
0.34
0.69
0.33
Q. 50
0.96
2.12
1.02
Q. 75
2.56
5.35
2.54
Máximo
102.7
58.32
18.78
Como se puede observar, el hecho de haber eliminado valores extremos ha hecho que los estadísticos de
primer y segundo orden se parezcan más a los reales. Sin embargo, obsérvese el máximo. Éste es ahora de
18.78, aún menor. Esto sugiere que las muestras de la segunda campaña deben ser consideradas. Por
tanto, consideraremos la opción 2, de desagrupamiento.
-
Posibilidad 2. “Desagrupamiento” de los datos
Para ello utilizaremos el programa DECLUS.EXE. Este programa asocia un peso a cada posición de
medida. Si el peso es <1, quiere decir que ese punto está agrupado con otros, y por tanto, no ofrece
demasiada información. Un peso >1 implica que el punto tiene una especial relevancia. El archivo de
parámetros para este programa se muestra en la Figura 15.
Figura 15. Archivo de parámetros para el programa DECLUS.EXE
Parameters for DECLUS
*********************
START OF PARAMETERS:
MEDIDAS.DAT
1 2 0 3
0.0 1.0e21
OUTPUT.SUM
OUTPUT.OUT
1.0 1.0
0
24 1.0 25.0
5
\Archivo de datos
\Columnas de x,y,z y variable
\Valores minimo y maximo a considerar
\Output con resumen
\Output con datos y pesos
\Anisotropia: y,z. Si sizex=10, entonces sizey=1.0*sizex
\0=look for min, 1 max
\num, min and max size
\num of origin offsets
Los parámetros de anisotropía marcan el tamaño de las celdas. Si las celdas son cúbicas (cuadradas en
este caso), deben fijarse a 1.0. Las dos últimas filas marcan donde (o mejor, hasta donde) deben buscarse
agrupamientos. Tal y como está fijado, se buscan a lo largo de todo el dominio.
El resultado del programa es un archivo, de formato análogo al de medidas, cuya última columna contiene
los pesos asociados a cada medida. Si ahora dibujamos el histograma de los datos “desagrupados”,
obtenemos el resultado de la Figura 16 y la Tabla 3.
Figura 16. Histograma y estadísticos de los datos “desagrupados”
Tabla 3. Comparación de los estadísticos “reales”, los de las medidas totales, las de la primera campaña y
las de ambas con los datos “desagrupados”.
Reales
Medidas
M. 1C
M-DES
n
2500
140
97
140
Media
2.58
4.35
2.21
2.52
Desv. St.
5.15
6.7
3.17
4.56
Mínimo
0.01
0.06
0.06
0.06
Q. 25
0.34
0.69
0.33
0.34
Q. 50
0.96
2.12
1.02
1.19
Q. 75
2.56
5.35
2.54
2.75
Máximo
102.7
58.32
18.78
58.32
Obsérvese que la media en éste caso es prácticamente la real, la desviación se parece mucho y hemos
recuperado el máximo de los datos. Así, queda demostrado que ésta es mucho mejor opción que la
primera.
Por el momento, sólo se ha hablado de estadísticos de la variable considerada. No obstante, siempre
conviene obtener el modelo de distribución estadístico (función de probabilidad) que mejor ajusta los
datos disponibles. De esta forma, siempre podremos conocer la probabilidad del suceso en los puntos no
muestreados.
Dado que, en este caso, conocemos la realidad, comenzaremos obteniendo la distribución de los valores
“reales” de la variable. Es conveniente siempre comenzar suponiendo que se trata de una variable con
función de densidad de probabilidad normal (Gaussiana) o log-normal. En casos en los que el ajuste de un
modelo Gaussiano no sea apto, deben probarse otras distribuciones (beta, geométrica, triangular, etc.).
Para verificar que la “realidad” obedece a un proceso Gaussiano, dibujaremos los valores en un papel de
probabilidad lognormal, mediante el programa PROBPLT.EXE, cuyo archivo de parámetros se presenta
en la Figura 17.
Figura 17. Archivo de parámetros para el programa PROBPLT.EXE
Parameters for PROBPLT
**********************
START OF PARAMETERS:
MEDIDAS_REALES.DAT
4 5
0.0 1.0e21
PROBREAL.PS
1
0.0 25.0 5.0
0.01 4
Prob Gauss REAL
\Archivo de datos
\Columna de variable y peso
\Limites de datos a considerar
\output PostScript file
\0=aritmetico, 1=log
\minimo,maximo,incremento en eje x: si aritmetico
\valor inicial,numero de ciclos : log
\Titulo
Figura 18. Representación en papel de probabilidad lognormal de las probabilidades del suceso “real”
Como se observa en la Figura anterior, la variable real obedece perfectamente a un proceso Gaussiano,
dado que los puntos se agrupan sobre una linea a 45º. Veamos si las medidas “desagrupadas” siguen el
mismo proceso. Para ello repetimos el procedimiento. El resultado se observa en la Figura 19.
Como se observa, también lo sigue, pero de forma más aproximada. De esta forma, podemos concluir que
lo mejor que se puede hacer con estos datos es desagruparlos. Resumiendo, parar representar la realidad,
contamos con 140 datos y sus respectivos pesos, siguiendo una función de densidad de probabilidad
Gaussiana, con los estadísticos que se muestran en la Tabla 4.
Tabla 4. Estadísticos y datos disponibles.
M-DES
n
140
Media
2.52
Desv. St.
4.56
Mínimo
0.06
Q. 25
0.34
Q. 50
1.19
Q. 75
2.75
Máximo
58.32
Figura 19. Representación en papel de probabilidad lognormal de las probabilidades del suceso
“muestreado”, una vez desagrupados los datos.
EL VARIOGRAMA EN GSLIB
El variograma es una medida muy general de la variabilidad espacial, y mide las diferencias entre un
punto no muestreado y un con medida que le sea cercano. De una forma más matemática, mide la
variabilidad de una variable aleatoria en dos posiciones distintas (de la varianza del cambio a una
distancia h). Para el ajuste del variograma, en primer lugar debe calcularse (y dibujarse) el variograma
muestral, analizarlo concienzudamente. Acto seguido, se propone un modelo de variograma, el cual
deberá validarse (este último punto queda fuera del alcance del presente tutorial).
En este primer paso, vamos a realizar el análisis del variograma muestral de la “realidad”, para conocer
cual debe ser la solución. Para ello, utilizaremos el programa GAM2M.EXE (cálculo) y VARGPLT.EXE
(dibujo). El archivo de parámetro de GAM2M.EXE se presenta en la Figuras 20. En la Figura 21 se
presenta parte del archivo de resultados. El programa GAM2M.EXE opera sobre mallas regulares, como
es el caso real. El programa VARGPLT.EXE no precisa de archivo de parámetros. En este caso, estamos
pidiendo a GAM2M.EXE que dibuje el semivariograma muestral en las direcciones norte-sur y esteoeste. El resultado de la aplicación sucesiva de dichos programas se presenta en la Figura 21, mientras
que en la Figura 22 se muestra parte del archivo de salida de GAM2M.EXE.
Figura 20. Archivo de parámetros para el programa GAM2M.EXE
Parameters for GAM2M
********************
START OF PARAMETERS:
MEDIDAS_REALES.DAT
1 1 0 0
-1.0e21 1.0e21
VAREXP_REAL.VAR
50 50 1
1.0 1.0
2 20
1 0
0 1
1
1 1 1
\ARCHIVO DE DATOS
\NUM. DE VAR Y COLUMNAS DONDE SE ENCUENTRAN
\LIMITES DE CORTE
\ARCHIVO DE SALIDA
\nx, ny, igrid
\xsiz, ysiz
\NUMERO DE DIRECCIONES Y NUMERO DE LAGS
\DIRECCION 1 (X)
\DIRECCION 2 (Y)
\NUMERO DE REPRESENTACIONES
\VAR DE COLA Y CABEZA. TIPO DE REPR.
Figura 21. Semivariogramas muestrales en las direcciones X Y. Medida de la variabilidad espacial de la
variable “real”.
Figura 22. Extracto del archivo de salida del programa GAM2M.EXE
NLAG
1
2
3
4
5
SEPA
1.000
2.000
3.000
4.000
5.000
SEMIV PARES
13.03226 2450
16.64981 2400
20.16062 2350
21.73316 2300
22.07451 2250
De la Figura 21 se infiere que el variograma modelo de la “realidad” puede ser un esférico, con pepita
9.0, meseta 25.0 y alcance 8.0, bastante isótropo. Para corroborar esta primera hipótesis, hecha “a mano”,
se podría superponer el variograma modelo sugerido en la figura anterior. Para dibujar el variograma
modelo, utilizaremos el programa VMODEL.EXE, cuyo archivo de parámetros se presenta en la Figura
23.
Figura 23. Archivo de parámetros del programa VMODEL.EXE
Parameters for VMODEL
*********************
START OF PARAMETERS:
vmodel.var
\output file of variograms
1 20
\ndir, nlag
1.0 0.0 0.0
\xoff(id),yoff(id),zoff(id)
1 9.00
\nst, nugget effect
1 8.0 16.0 n
\it,aa,cc:
0.0 0.0 0.0 1.0 1.0
\ang1,ang2,ang3,anis1,anis2:
Con este archivo de parámetros estamos pidiendo la representación de un variograma esférico (it=1) con
una única estructura, con pepita 9, alcance 8 y meseta (16+9=25), completamente isótropo.
La Figura 24 muestra la superposición de este variograma modelo con los experimentales obtenidos
anteriormente. Como se ve, el ajuste es muy bueno.
Figura 24. Ajuste entre variograma modelo y variograma experimental
Debería hacerse ahora lo mismo pero con el juego de medidas “desagrupado”. Como se va a observar, el
agrupamiento o “clustering” no solo afecta a la estadística univariada, sino también a la bivariada. Para
ello, vamos a intentar ajustar un modelo de variograma a los 140 datos de las dos campañas (140 en total).
Dado que ahora las medidas se encuentran dispersas y no sobre una malla regular, no podemos utilizar el
programa GAM2M.EXE, sino que utilizaremos el GAMV2M.exe, cuyo archivo de parámetros se muestra
en la Figura 25. Lo único que los diferencia es la irregularidad en la distribución de los datos.
Figura 25. Archivo de parámetros para el programa GAMV2M.EXE.
Parameters for GAMV2M
*********************
START OF PARAMETERS:
MEDIDAS.DAT
1 2
1 4
-1.0e21 1.0e21
VAREXP_140.VAR
10
4.0
2.0
2
0.0 90.0 50.0
90.0 22.5 10.0
1
1 1 1
\data file
\columns for x and y coordinates
\nvar; column numbers...
\tmin, tmax (trimming limits)
\output file for variograms
\nlag - the number of lags
\xlag - unit separation distance
\xltol- lag tolerance
\ndir - number of directions
\azm(i),atol(i),bandw(i)i=1,ndir
\number of variograms
\tail, head, variogram type
El resultado es el variograma experimental de los 140 datos, que se muestra en la Figura 26.
Figura 26. Variograma experimental de los datos de las dos primeras campañas.
Como se puede observar, la falta de datos distorsiona terriblemente el variograma experimental (con
respecto al experimental “real” obtenido anteriormente). Una comparación entre los valores de ambos se
muestra en la Tabla 5.
Tabla 5. Comparación de los parámetros “de visu” de los variogramas experimentales obtenidos con
2500 datos y con los 140 correspondientes a las dos primeras campañas.
Datos
2500
140
Modelo
Esférico
Esférico
Pepita
9
0.3
Alcance
8
10
Meseta
25
20
Como se puede observar, el variograma modelo se conserva (no tiene porque pasar). La pepita se reduce
sobremanera. Esto es bastante normal si se tiene en cuenta cual es el significado de la pepita del
variograma. Mide la variabilidad a pequeña escala. Dado que no se puede cuantificar al eliminar una
ingente cantidad de medidas, esa pepita tiende a desaparecer. El alcance se mantiene, dado que nuestro
juego de medidas esta bastante bien situado. La meseta (análoga, más o menos, a la varianza muestral es
también parecida).
En la Figura 27 se muestra el variograma experimental obtenido, superpuesto con el variograma modelo
sugerido y con el obtenido anteriormente para las 2500 medidas.
Figura 27. Superposición de variogramas experimentales y modelos.
Una vez se tiene una función (el variograma en este caso) que describe la variabilidad espacial del
problema, pueden utilizarse las herramientas que ofrecen información sobre el campo: estimación
condicionada (kriging), simulación condicionada/ no condicionada.
ESTIMACIÓN CONDICIONADA (KRIGING)
Una vez se tiene la descripción del variograma (modelo, alcance, anisotropía, meseta y pepita), puede
llevarse a cabo una “interpolación” en los puntos no muestreados, en base a ese/esos variograma/s y a las
medidas disponibles. Como se comentó en la clase anterior, el gran problema que tiene GSLIB es el
trabajo en base a una malla regular. Portanto, no vamos a realizar en los puntos que nosotros queramos,
sino en el centro de gravedad de las celdas. El programa que se va a utilizar es KTB3D.EXE para realizar
krigeados de variable única. Si se desea cokrigear, deberá usarse el programa COKB3D.EXE, de
funcionamiento muy similar (simplemente hay que definirle las medidas de las variables secundarias y los
variogramas de estas, además de los cruzados con la primaria). El resultado de estos programas es doble.
Por un lado, genera el valor de la estimación en los centros de gravedad de los pixeles, además de la
varianza de estimación. Por el otro, genera un archivo de “debugging”, en el que se lista los puntos de
medida y los pesos asociados utilizados en la interpolación de un punto determinado.
Para visualizar los resultados pueden usarse los programas CSCALE.EXE (explicado en la clase anterior)
o GSCALE (para mapas de grises,d e funcionamiento análogo). Veamos el archivo de parámetros del
programa KT3D, mostrado en la Figura 28.
Figura 28. Archivo de parámetros del programa KTB3D.EXE
Parameters for KTB3D
********************
START OF PARAMETERS:
DATOS.DAT
1 2 0 3
-1.0e21 1.0e21
ESTIM.OUT
1
CHECK.DBG
50 0.5 1.0
50 0.5 1.0
1 0.5 1.0
1 1 1
4 16
0
20.0
0.0 0.0 0.0 1.0 1.0
0 4.35
000000000
0
0
5
NADA.DAT
4
1 0.3
1 10.0 20.0
0.0 0.0 0.0 1.0 1.0
\ARCHIVO CON LAS MEDIDAS
\COLUMNAS CON X,Y,Z Y VARIABLE
\LIMITES DE CORTE
\ARCHIVO DE RESULTADOS
\NIVEL DE DEBUGGING: 0,1,2,3
\ARCHIVO DE DEBUGGING
\NX,XMN,XSIZ
\NY,YMN,YSIZ
\NZ,ZMN,ZSIZ
\PUNTOS DE DISCRETIZACIÓN DE UN BLOQUE
\MIN Y MAX DE DATOS PARA EL SISTEMA DE KRIGING
\A RETENER POR OCTANTE (0:NO SE USA)
\SEMIEJE MAYOR DE BUSQUEDA
\ANGULOS Y ANISOTROPIAS DEL ELIPSOIDE DE BUSQUEDA
\0=KRIGING ORDINARIO; 1=KRIG. SIMPLE + MEDIA
\TENDENCIA POLINOMICA (0:INACTIVA); x,y,z,xx,yy,zz,xy,xz,zy
\0, ESTIMAR LA VARIABLE; 1, ESTIMAR LA TENDENCIA
\1: CONSIDERAR DERIVA EXTERNA
\COL DE LA DERIVA EN DATOS.DAT (SI 1 EN LA ANTERIOR)
\ARCHIVO CON LA DERIVA CELDAS DE LA MALLA
\NUMERO DE COLUMNA EN ESE ARCHIVO
\NUMERO DE ESTRUCTURAS, PEPITA
\TIPO, ALCANCE MAYOR,(MESETA-PEPITA)
\ANG1,ANG2,ANG3,ANIS1,ANIS2
El resultado de la ejecución de KTB3D.EXE es doble; por un lado, se muestra en la Figura 29 los valores
de la estimación y de la varianza de estimación que ofrece el programa.
Figura 29. Estimación y varianza de estimación para el archivo de parámetros anterior
KTB3D ESTIMATES WITH: Clustered 140 primary and secondary data
2
Estimate
EstimationVariance
4.693 0.791
4.041 0.642
2.885 0.539
2.255 0.538
1.622 0.537
1.066 0.533
1.200 0.621
1.394 0.738
......
Nótese que, al trabajar sobre una malla regular, debe seguirse la ordenación de pixeles descrita en la clase
anterior. Por otro lado, la Figura 30 muestra parte del archivo de ‘debugging’, correspondiente a la
estimación del primero de los pixeles
Figura 30. Extracto del archivo de debugging
BLOCK:
1
1
1 at 0.5000000
0.5000000
0.5000000
Lagrange : -0.170163970157926
BLOCK EST: x,y,z,vr,wt
2.500
1.500
0.500
3.330
0.634
5.500
1.500
0.500
0.060
0.118
0.500
7.500
0.500
12.740
0.095
0.500
8.500
0.500
6.490
0.031
1.500
8.500
0.500
20.350
-0.010
2.500
8.500
0.500
8.900
-0.015
0.500
9.500
0.500
15.770
0.049
1.500
9.500
0.500
7.560
0.016
2.500
9.500
0.500
6.260
0.021
3.500
9.500
0.500
7.920
0.062
estimate, variance 4.692778
0.7912890
El resultado gráfico de la aplicación del programa, tras ejecutar CSCALE.EXE se muestra en la Figura
31. Uno de los resultados más importantes a remarcar es el bajo valor de los valores esperados
(recuérdese que el kriging no es más que un sistema de interpolación y que el máximo de los datos
utilizados es 58). Otro resultado importante es la suavidad inherente al campo, debido al uso de éste (o
cualquier otro sistema de interpolación). Si lo que se pretende es obtener un mapa que represente la
variabilidad espacial de manera menos suave, debe utilizarse un algoritmo de simulación. Obsérvese
además que hay puntos “en blanco”. Los valores interpolados en dichos puntos son negativos.
La Figura 32 muestra el campo de la varianza de estimación. Lógicamente los valores menores de
varianza de estimación son los asociados a los pixeles próximos (o que contienen) a los puntos de medida.
Figura 31. Resultado gráfico del krigeado ordinario
Figura 32. Varianza de estimación del campo krigeado