puntos óptimos (singulares, estacionarios…)
Anuncio

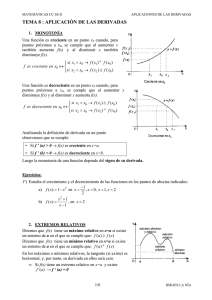
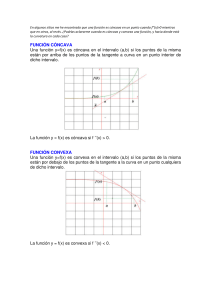
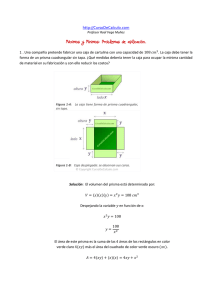
PUNTOS ÓPTIMOS (SINGULARES, ESTACIONARIOS…). MÁXIMOS Y MÍNIMOS. Máximo y mínimo global o absoluto. Extremos absolutos. Tenemos una función f(x) € D ( dominio) Un punto c € D se dice máximo ( global o absoluto) si el valor de la función en dicho punto no es superado por ningún otro valor de la función en cualquier otro punto. F ( c) ≥ f( x) Un punto c € D se dice mínimo ( global o absoluto) f ( c) ≤ f( x) Los valores máximos y mínimos absolutos o globales de una función se hallan sobre todo su dominio Máximos y mínimos locales. Extremos relativos. “Ahora nos interesa calcular máximos y mínimos no de la función en todo su dominio sino de un entorno de la función” 1 La función f tiene un máximo local en c si existe un intervalo ( a, b) centrado en c tal que f(c ) ≥ f( x) para todo x € D ( a, b) La función f tiene un mínimo local en c si existe un intervalo ( a, b) centrado en c tal que f(c ) ≤ f( x) para todo x € D ( a, b) ¿CÓMO DETERMINAR ESOS VALORES? 1. CONDICIÓN NECESARIA DE EXISTENCIA DE MAX Y MIN→Existencia de puntos estacionarios. Observando la gráfica vemos que a, b, c y d son puntos máximos y mínimos. ¿Qué tienen en común? Que su tangente en esos puntos de la gráfica es paralela al eje X. Por lo tanto su pendiente es 0. O, dicho de otra forma, la derivada de la gráfica en dichos puntos es igual a 0. F’ (x0) = 0 2 FORMA DE CALCULAR MÁXIMOS Y MÍNIMOS: TEST DE LA PRIMERA DERIVADA TEST DE LA SEGUNDA DERIVADA TEST DE LAS DERIVADAS SUCESIVAS TEST DE LA PRIMERA DERIVADA. (Estudio del crecimiento y decrecimiento de una función) (Estudio de la inversión del sentido de crecimiento) Si c es un punto máximo: A la izda la función crece → f’ (x0) ≥ 0 A la dcha la función decrece → f’ (x0) ≤ 0 Si c es un punto mínimo : A la izda la función decrece → f’ (x0) ≤ 0 A la dcha la función crece → f’ (x0 )≥ 0 3 TEST DE LA SEGUNDA DERIVADA: Si f’’ ( x0 ) < 0 ; x0 es un máximo local Si f’’ ( x0 ) > 0 ; x0 es un mínimo local Si f’’ (x0 ) = 0 ¿¿?? ( Test de las derivadas sucesivas) Este criterio tiene la ventaja de su fácil y rápida aplicación, por ello, es más utilizado que el anterior. 4 TEST DE LAS DERIVADAS SUCESIVAS Supongamos que f’ (x0) = f’’(x0) = f’’’ (x0) =…..= fn-1’ (x0) = 0 y fn’ (x0) ≠ 0 , entonces se cumple: Si n es par y fn’ (x0) < 0 ; x0 es un máximo local de f Si n es par y fn’ (x0) >0 ; x0 es un mínimo local de f Si n es impar x0 es un punto de inflexión ( la curva pasa de ser cóncava a convexa , o al revés) Además podemos obtener información sobre el comportamiento de la curva en un entorno del punto ( CONCAVIDAD Y CONVEXIDAD): Si n es par y fn’ (x0) < 0 ; f es cóncava en un entorno de f Si n es par y fn’ (x0) >0 ; f es convexa en un entorno de f. Si n es impar x0 es un punto de inflexión ( la curva pasa de ser cóncava a convexa , o al revés) 5