UNIDAD 9: UTILICEMOS LAS FUNCIONES ALGEBRAICAS

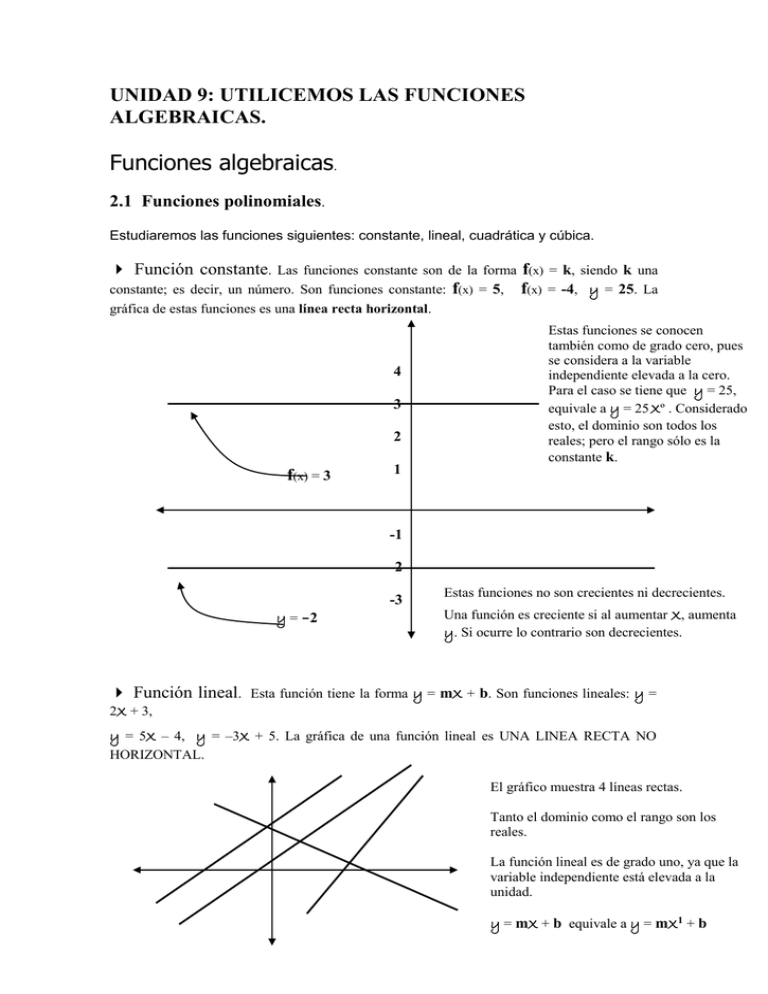
UNIDAD 9: UTILICEMOS LAS FUNCIONES
ALGEBRAICAS.
Funciones algebraicas.
2.1 Funciones polinomiales.
Estudiaremos las funciones siguientes: constante, lineal, cuadrática y cúbica.
 Función constante.
Las funciones constante son de la forma f(x) = k, siendo k una
constante; es decir, un número. Son funciones constante: f(x) = 5, f(x) = -4, y = 25. La
gráfica de estas funciones es una línea recta horizontal.
4
3
2
f(x) = 3
1
Estas funciones se conocen
también como de grado cero, pues
se considera a la variable
independiente elevada a la cero.
Para el caso se tiene que y = 25,
equivale a y = 25 Xº . Considerado
esto, el dominio son todos los
reales; pero el rango sólo es la
constante k.
-1
-2
-3
y = -2
 Función lineal.
Estas funciones no son crecientes ni decrecientes.
Una función es creciente si al aumentar X, aumenta
y. Si ocurre lo contrario son decrecientes.
Esta función tiene la forma y = mX + b. Son funciones lineales: y =
2X + 3,
y = 5X – 4, y = –3X + 5. La gráfica de una función lineal es UNA LINEA RECTA NO
HORIZONTAL.
El gráfico muestra 4 líneas rectas.
Tanto el dominio como el rango son los
reales.
La función lineal es de grado uno, ya que la
variable independiente está elevada a la
unidad.
y = mX + b equivale a y = mX1 + b
 Significado de b en la función lineal.
Observa cada una de las rectas siguientes:
y=X+2
y=X
2
y=X–1
1
–1
y=X+1
y=X–2
–2
Las funciones de las rectas anteriores son:
y=X+2
y=X+1
y=X
y=X–1
y=X–2
Podemos observar que el valor de b coincide con el
punto en el que la recta corta al eje y.
Precisamente b es donde la recta intercepta al eje y.
A b se le conoce también como intercepto. En el
intercepto, X = 0.
 Significado de m en la función lineal.
y = 3X + 1
y = 2X +
Las ecuaciones de las rectas de la
1 derecha son:
y=X+1
y = 2X + 1
y = 3X + 1
y = -3X + 1
y = -2X + 1
y = -X + 1
y = -3X + 1
y = -2X + 1
y = -X + 1
y=X+1
Podemos observar que todas las rectas tienen el mismo intercepto, pero el valor de m es
distinto. Efectivamente, m es la pendiente de la recta. Observa que la pendiente puede ser
negativa. Cuando m es positiva, el ángulo de inclinación es menor de 90º. Cuando es negativa,
está entre 90º y 180º.
 Gráfica de una función lineal.
Para graficar una línea recta bastan 2 puntos. Si se desea, uno de ellos puede ser el intercepto.
Para calcular el otro, se le da cualquier valor a X.
Ejemplo. Graficar las rectas y = 2X + 3
y y = -3X – 2. Determinar si son crecientes o no
lo son.
Para y = 2X + 3 el intercepto es (0, 3) Encontremos otro punto dándole a X el valor de 1.
Obtenemos el punto (1, 5)
Para y = -3X – 2 el intercepto es (0, –2) Encontremos otro punto dándole a X el valor de 1.
Obtenemos el punto (1, –5)
5
y = 2X + 3
4
3
2
1
1
2
-1
-2
-3
y = -3X – 2
-4
-5
La recta y = 2X + 3 es creciente: al aumentar X aumenta y. En cambio la recta y = -3X – 2 es decreciente:
al aumentar X, disminuye y. Veamos dos puntos:
para X = 1, y = -5; para X = 2, y = -8.
En general, si la pendiente es positiva, la recta es creciente; si la pendiente es negativa, la recta es
decreciente.
 La pendiente de una recta en grados.
El ángulo que una recta forma con el eje X se puede calcular mediante la función tangente
inversa. Esto es así debido a que la pendiente de una recta es la tangente del ángulo que forma
con el eje X.
Para el caso de y = 2X + 4, la pendiente 2 es la tangente del ángulo que forma esta recta con el
eje X. Veamos esto gráficamente.
Se tiene que: Tan β = opuesto / adyacente = 4/2 = 2
y = 2X + 4
(Hemos tomado 2 y no –2)
En la recta y = 2X + 4, 2 es la pendiente.
4
Se tiene que: β = Tan-1(2) = 63.4º, este es el ángulo que forma la recta
con el eje X.
β
-2
 Actividad 2. Utilizando papel milimetrado, trazar las rectas siguientes:
2. y = 2X + 5
-X – 2
3. y = 2X + 8
4. y = 2X + 2
5. y = 3X + 2
1. y = 2X + 3
6. y = 4X + 2
7. y =
8. y = -2X – 2 9. y = -3X – 2
 discusión 2
. 1. Utilizando papel milimetrado, grafiquen en un mismo plano las
rectas
y = 1.5X + 2 y y = -2.5X + 10 y encuentren el punto en el cual chocan.
2. Se sabe que las rectas y = 2X + 3 y y = 2X + 5 nunca se cortan. Discutan y traten de
encontrar la explicación de tal fenómeno.
 Funciones cuadráticas.
Estas funciones son de segundo grado: la variable independiente está al cuadrado. La
gráfica de estas funciones se conocen como parábolas. Estas pueden abrirse hacia
arriba o hacia abajo.
El lanzamiento de un objeto
describe una parábola. Cuando el
portero lanza el balón, éste
describe una parábola.
Vértice
Abierta hacia arriba
Abierta hacia abajo
Una parábola está abierta hacia arriba si el coeficiente de X2 es positivo; de lo contrario se abre
hacia abajo.
El dominio de una parábola son los reales; pero el rango tiene siempre una restricción. Esto se
debe a que una parábola parte de un punto hacia el + ∞ o el – ∞. Esto significa que el rango
será
[k, +∞[ o ] -∞, k] Aquí k es la componente en y del vértice.
El vértice de una parábola puede estar sobre el eje y o en cualquier otro punto en el plano. Las
parábolas de la forma y = aX2 + k, tienen el vértice en y = k. Si k = 0, la parábola está en el
origen.
Las funciones de la forma y = aX2 + bX + c, tienen el vértice en cualquier punto del plano. Si se
trata de un trinomio cuadrado perfecto, el vértice está sobre el eje X.
 Gráfica de una parábola.
Para graficar una parábola, debemos calcular su vértice, los puntos donde corta al eje X (si lo
corta) y el punto donde corta al eje y.
Recuerda que... si hacemos X = 0, encontramos el punto o puntos donde la curva corta a y; y si
hacemos y = 0, encontramos el punto o puntos donde la curva corta a X.
Ejemplos. Encontrar el rango y la gráfica de:
3. y = -X2 + 8X – 12
1. y = 4 – X2
2. y = X2 + 2
4. y = X2 – 4X + 4
 Solución.
 y = 4 – X2
La parábola se abre hacia abajo, y tiene su vértice en y = 4. Se concluye que
corta al eje X. ¿Dónde? Donde y = 0,
y = 4 – X2  4 – X2 = 0  – X2 = – 4  X2 = 4  X = ± 4  X = ± 2
 Observa que aquí tomamos las 2 raíces: 2 y –2.
La parábola corta a X en 2 y –2. El gráfico es el siguiente:
Del gráfico se concluye que el rango es ]-∞, 4]
4
Como el rango son los valores que puede tomar la y, puede
calcularse despejando X. Al despejarla de
y = 4 – X2, obtenemos: X = 4 – y . Se aprecia que y
tiene que ser menor o igual a 4.
Además, de -∞ a cero, la función es creciente; de cero en
adelante es decreciente. Observemos que pasa de creciente
a decreciente en el vértice.
-2
2
 y = X2 + 2
Esta parábola se abre hacia arriba, y tiene su vértice en y = 2. Se concluye que
NO corta al eje X. El gráfico es:
Del gráfico se concluye que el rango es [2, +∞ [
Esto se aprecia al despejar X de y = X2 + 2:
X = √y – 2 Aquí y debe de ser 2 o mayor que 2.
Además, de -∞ a cero, la función es decreciente; de cero en
adelante es creciente. Observemos que el vértice marca el
cambio. En general, si una recta tangente a la curva tiene
pendiente positiva, la función es creciente; de lo contrario es
decreciente.
2
Recta tangente
 y
= -X2 + 8X – 12
Esta parábola se abre hacia abajo. Al aplicar la fórmula general
obtenemos que sus raíces son: 2 y 6. Estos son los valores que hacen cero la ecuación; es decir,
son los valores donde la curva corta al eje X.
La parábola, abriéndose hacia abajo, corta al eje X en 2
y 6. Significa que el vértice tiene como coordenada en
X el punto medio de 2 y 6, que es 4. Al sustituir 4 en la
función, se obtiene:
2
6
y = -X2 + 8X – 12 = -(4)2 + 8(4) – 12 = 4
El vértice está en (4, 4)
El gráfico es el siguiente:
Aquí puede apreciarse que el rango es: ]∞, 4]
4
En este caso NO puede despejarse X de y
= -X2 + 8X – 12. Es decir que por ese
método no se puede calcular el rango.
Determina tú dónde es creciente o
decreciente.
2
4
6
Esta parábola corta al eje y en y = –12. A esto se llega al hacer X = 0 en y = -X2 + 8X – 12.
El punto (0, -12) no aparece en la gráfica por falta de espacio.

y = X2 – 4X + 4
Esta función es un
trinomio cuadrado perfecto. La raíz es 3.
Significa que sólo en X = 3 corta al eje X. Allí
mismo tiene su vértice. Además, al hacer X = 0,
obtenemos y = 4. La curva pasa por (0, 4)
El gráfico es una parábola que se abre hacia
arriba.
4
En el gráfico puede apreciarse que el rango es:
[0, +∞ [
Es decreciente antes de 3. Después de 3 es
creciente.
3
 Actividad 3.
Para cada función
determinar el rango, gráfico, intervalos donde es creciente o decreciente. 1. y = X2 – 1 2. y
= 1 – X2
3. y = X2– 9
4. y = 9 – X2
5. y = X2 + 3
6. y = –X2 – 3
7. y = X2 – 2X – 8
8. y = –X2 + 2X + 8
9. y = X2 – 4X – 5
10. y = –X2 + 4X + 5
 discusión 3
al eje X la función y =
. Determinar el rango y el gráfico, destacando los puntos donde corta
X2–
3.
 Funciones cúbicas.
Estas funciones son de tercer grado: la variable independiente está al cubo. En estas
funciones, el rango y el dominio son los reales.
No ahondaremos en este tipo de funciones. Sin embargo, sus gráficos pueden tener
las formas siguientes:





El gráfico  puede ser y = X3; en tal caso, el gráfico  sería y = –X3. El gráfico  no pasa
por el origen. Corresponde a una cúbica de la forma y = X3 – k. El gráfico  corta al eje X en
2 puntos. El gráfico  corta al eje X en 3 puntos. Estos 2 últimos gráficos corresponden a
funciones que incluyen X o X2.
 discusión 4
. Utilizando papel milimetrado trazar las gráficas siguientes:
1. y = X3 – 5X2 + 7X – 3. Utiliza la siguiente tabla de valores:
X
–1
0
1
2
3
4
y = X3 – 5X2 + 7X – 3
2. y = X3 – 6X2 + 11X – 6. Utiliza la siguiente tabla de valores:
X
–0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
y = X3 – 6X2 + 11X
–6
2.2 Función raíz cuadrada.
La función raíz cuadrada ya se estudió en Funciones reales y de variable real,
en la página 76. Allí se estudió Dos clases de funciones con dominio
restringido.
2.3 Función de proporcionalidad inversa.
La función de proporcionalidad inversa también se estudió en Funciones reales y de
variable real. Esta es una función con dominio restringido. Es cuando la variable
independiente aparece en el denominador. Como el denominador no puede tomar el valor de
cero, aparecen las asíntotas.
Las funciones de proporcionalidad inversa tienen la forma y = k/X. Siendo k una constante. Son
funciones de proporcionalidad inversa:
y = 5/X
y = 4/(X – 2)
 discusión 5
y = k/( X + 3 )
y = k/(2 – X)
. Graficar la función 1/ X.
Soluciones.
Actividad 1.
1. D = [0, +∞[ R = [3, +∞[ 2. D = [0, +∞[ R = [5, +∞[ 3. D = [0, +∞[ R =
[-2, +∞[
4 D = [0, +∞[ R = [-4, +∞[ 5. D = [0, +∞[ R = [-5, +∞[ 6. D = ]-∞, 0] R =
[3, +∞[
7. D = [3, +∞[ R = [0, +∞[ 8. [2, +∞[ R = [0, +∞[ 9. D = ]-∞, 4] R = [0,
+∞[
10. D = ]-∞, - 4] R = [0, +∞[ 11. D = [0, +∞[ R = ]-∞, 2] 12. D = [0, +∞[
R = ]-∞, -2] 13. D = ]-∞, - 3]+[2, +∞[ R = [0, +∞[ 14. D = ]-∞, - 4]+[2,
+∞[
R = [0, +∞[
15. D = ℜ excepto 3 y –3 R = ℜ excepto ] -1, 0] (ver gráfico) 16. D = ℜ
excepto 3 y –3 R = ℜ excepto [0, 1[ La gráfica es la anterior invertida 17. D = ℜ excepto
-3 y 2 R = ℜ excepto [ 0, 0.96[ Las raíces de la cuadrática son –3 y 2. Entre ellos el punto
medio es –0.5: aquí tiene su vértice la parábola; es decir que aquí arranca. Para este valor, y
vale 0.96. La parábola corta al eje y en 1. (ver gráfico) 18. D = ℜ excepto -3 y 2 R = ℜ
excepto ] -0.96, 0] Las raíces de la cuadrática son –3 y 2. Entre ellos el punto medio es –0.5:
aquí tiene su vértice la parábola; es decir que aquí arranca. Para este valor, y vale -0.96. La
parábola corta al eje y en -1. El gráfico es el anterior invertido. 19. D = ℜ excepto -5 y 3 R =
ℜ excepto ] -0.9375, 0] Las raíces de la cuadrática son –5 y 3. Entre ellos el punto medio es –
1: aquí tiene su vértice la parábola y se abre hacia abajo. Para este valor, y vale -0.9375. La
parábola corta al eje y en -1. 20. D = ℜ excepto -5 y 3 R = ℜ excepto ] 0 , 0.9375] La
parábola y se abre hacia arriba. Para este valor, X = -1, y vale 0.9375. La parábola corta al eje y
en 1. El gráfico es el anterior invertido.
Gráfico 15
Gráfico 17
El eje y es cortado en -1
X = -3
X = -3
X=3
X=2
discusión 1.
Dominio = ℜ excepto –2, 0, 2 y 3
discusión 2.
1. Chocan en el punto (2, 5)
2. Nunca se cortan porque tienen igual pendiente (2). Es decir que son paralelas.
Actividad 3.
1. Rango = [-1, +∞[ Decreciente hasta 0, luego es creciente. La parábola tiene el vértice en
y = -1. Corta al eje X en –1 y 1. 2. R = ]-∞, 1] Creciente hasta 0, luego es decreciente. La
parábola tiene el vértice en y = 1. Corta al eje X en –1 y 1. 3. R = [-9, +∞[ Decreciente
hasta 0, luego es creciente. La parábola tiene el vértice en y = -9. Corta al eje X en –3 y 3. 4.
R=
]-∞, 9]
Creciente hasta 0, luego es decreciente. La parábola tiene el vértice en y = 9.
Corta al eje X en –3 y 3. 5. R = [3, +∞[ Decreciente hasta 0, luego es creciente. La
parábola tiene el vértice en y = 3. No corta al eje X 6. R = ]-∞, -3] Creciente hasta 0,
luego es decreciente. La parábola tiene el vértice en y = -3. No corta al eje X. 7. R = [-9,
+∞[ Decreciente hasta X = 1, luego es creciente. La parábola tiene el vértice en el punto (1, 9) Corta al eje X en –2 y 4. Al eje y lo corta en -8
8. R = ]-∞, 9] Creciente hasta X = 1, luego es decreciente. La parábola tiene el vértice en el
punto (1, 9) Corta al eje X en –2 y 4. Al eje y lo corta en 8. 9. R = [-9, +∞[ Decreciente
hasta X = 2, luego es creciente. La parábola tiene el vértice en el punto (2, -9) Corta al eje X en
–1 y 5. Al eje y lo corta en –5. 10. R = ]-∞, 9] Creciente hasta X = 2, luego es
decreciente. La parábola tiene el vértice en el punto (2, 9) Corta al eje X en –1 y 5. Al eje y lo
corta en 5.
discusión 3.
R=
[-3, +∞[
Decreciente hasta X = 0, luego es creciente. La parábola tiene el vértice en el
punto (0, -3) Corta al eje X en –√3 y
√3.
discusión 4.
1. Resulta una gráfica que corta a y en –3 y al eje X en 1 y 3.
2. Resulta una gráfica que corta a y en –6 y al eje X en 1, 2 y 3.
1
2
1
-3
2
3
discusión 5.