La función es una parábola, como se muestra en la figura 1

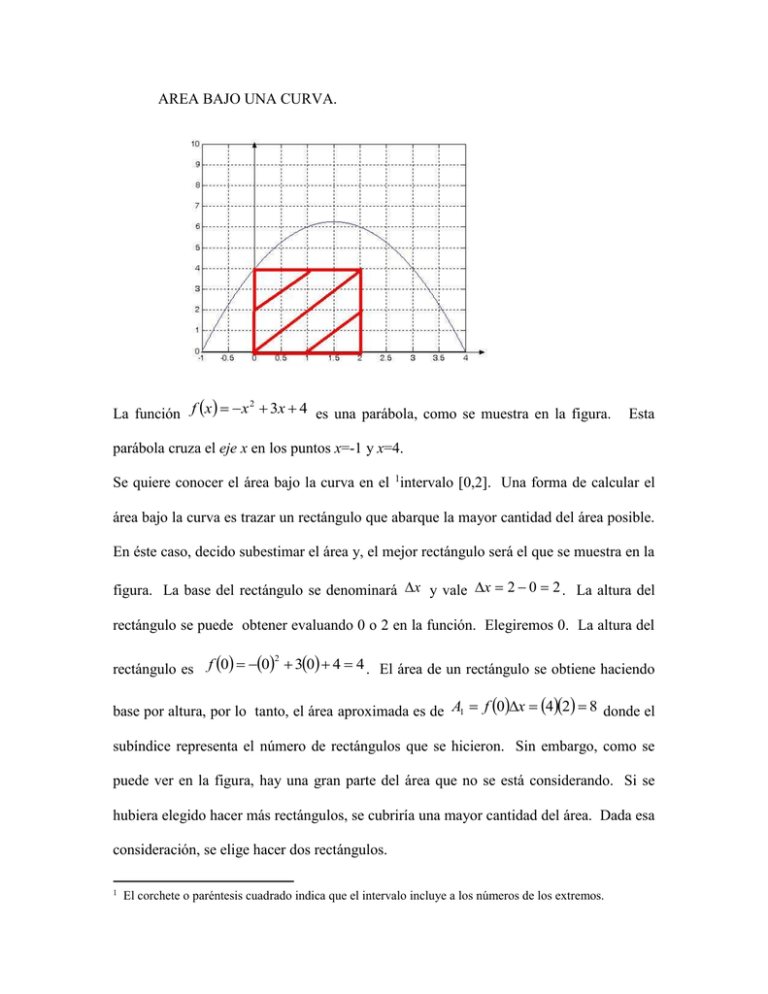
AREA BAJO UNA CURVA.
2
La función f x   x  3x  4 es una parábola, como se muestra en la figura.
Esta
parábola cruza el eje x en los puntos x=-1 y x=4.
Se quiere conocer el área bajo la curva en el 1intervalo [0,2]. Una forma de calcular el
área bajo la curva es trazar un rectángulo que abarque la mayor cantidad del área posible.
En éste caso, decido subestimar el área y, el mejor rectángulo será el que se muestra en la
figura. La base del rectángulo se denominará x y vale x  2  0  2 . La altura del
rectángulo se puede obtener evaluando 0 o 2 en la función. Elegiremos 0. La altura del
rectángulo es f 0  0  30  4  4 . El área de un rectángulo se obtiene haciendo
2
base por altura, por lo tanto, el área aproximada es de A1  f 0x  42  8 donde el
subíndice representa el número de rectángulos que se hicieron. Sin embargo, como se
puede ver en la figura, hay una gran parte del área que no se está considerando. Si se
hubiera elegido hacer más rectángulos, se cubriría una mayor cantidad del área. Dada esa
consideración, se elige hacer dos rectángulos.
1
El corchete o paréntesis cuadrado indica que el intervalo incluye a los números de los extremos.
Si se tiene un intervalo de 2 unidades y se quieren hacer 2 rectángulos, la base de cada
x 
rectángulo estará dada por
int ervalo
2
x   1
num erode rec tan gulos que en este caso es
2
y, por lo tanto, la base de cada rectángulo es 1. Ahora, ¿cómo calcular la altura?
Analizando la gráfica se puede observar que la altura está dada por el valor de la función
en x=0 y en x=1. Esto es, en x  0x y en x  1x . Así, el primer rectángulo tiene
f 0  0  30  4  4
2
una altura de
y el segundo tiene una altura de
f 1  1  31  4  6 . El área va a ser la suma del área de ambos rectángulos, por lo
2
tanto, A2  f 0x  f 1x  41  61  10 .
Aunque el resultado todavía no es
exacto, hemos cometido un error menor en el cálculo del área.
Es obvio, entonces, que mientras más rectángulos se hagan, mejor va a ser el área.
x 
Generalizando, la base la obtenemos haciendo
int ervalo
num erode rec tan gulos y si vamos a
hacer ‘n’ rectángulos en el intervalo [0,2], entonces
x 
20 2

n
n . La altura de cada
rectángulo la obtendremos evaluando la función en kx donde k tomará valores desde
cero hasta n-1. Por ejemplo, sea n=10 rectángulos,
La última columna representa el área de cada uno de los 10 rectángulos. El área total será
su suma A10  11.12 . Este valor da una mejor aproximación al área bajo la curva. Sin
embargo, sigue habiendo error. Si se lograra hacer un número infinito de rectángulos,
entonces, el error sería prácticamente cero, por lo tanto, la base de cada rectángulo será
x 
20 2

n
n
y la altura es la función evaluada en cada kx para k=0 hasta n-1. Sin embargo, es más
conveniente pensar en que sea cada k 1x para k=1 hasta n. Así, la altura es
f k  1x   k  1x   3k  1x  4
2
f k  1x   k  1 x 2  3k  1x  4
2
Esto quiere decir que la altura del cuarto rectángulo suponiendo que se hacen 10
rectángulos (comparar con la tabla anterior) sería para k=4 y n=10:
f 3x   3 x 2  33x  4
2
f 3x   9x 2  9x  4
  2 
2
2
f  3    9   9   4
 10 
 10 
  10  
2
6
 4  2
f    9
  9   4  5.44
 10 
 100  10 
Retomemos, ahora, para n rectángulos. El área por debajo de la función será la suma del
área de los n rectángulos, por lo tanto,
n
An   xf k  1x 
k 1
lo cual significa la suma de los productos de base por altura. x no depende del índice
x 
de la sumatoria ya que
2
n , por lo tanto,
n
An  x f k  1x 
k 1
2
y sabemos que f k  1x  k  1 x  3k  1x  4 , entonces, se sustituye
2
n


An  x  k  1 x 2  3k  1x  4
k 1
2
Se resuelven los productos
n


An  x  k 2 x 2  2kx 2  x 2  3kx  3x  4
k 1
Agrupamos a los términos que no tienen k (índice de la sumatoria)
n

 
An  x  k 2 x 2  2kx 2  3kx   x 2  3x  4

k 1
y se separan las sumatorias
n


n


An  x  k 2 x 2  2kx 2  3kx  x  x 2  3x  4
k 1
k 1
En la segunda sumatoria, el argumento está conformado únicamente por constantes y
n
dado que
 c  nc
j 1
  x
n
, entonces
k 1
2
 

 3x  4   x 2  3x  4 n
.
Esto se sustituye en An


n

An  x  x 2  3x  4 n  x  k 2 x 2  2kx 2  3kx

k 1
x 
Con anterioridad se había dicho que
2
n , por lo tanto,
2
2
2
 2   2 
 2    2  n  2 2 
2
 2 
An        3   4 n     k    2k    3k  
 n    n 
 n    n  k 1 
n
n
 n 
Resolviendo las multiplicaciones del primer término y factorizando en el segundo
 2  4 6
 2
An    2   4 n   
n
 n  n
 n
 4 6
 4
An  2  2   4   2
n
 n
 n
An  
y se sabe que
2 n

  k
k 1

 2k 2  4

  2

n
k 1  n 
n
8 12
8
 8 3
2
n
n
n
n
k 2 
k 1
2

2
2
   2k    3k 
n
n

 4k  4
  2

n
k 1  n 
n
16 n
12 n
k

k
 n2 
n 3 k 1
k 1
n
 3k 
k 1
n
 k 1  2  3  ...  n 
k 1
n
k
2
nn  1
2
1  4  9  ...  n 2 
k 1
nn  12n  1
6
 nn  1
k 3 1  8  27  ...  n 3  


 2 
k 1
n
2
por lo tanto,
An  
8 12
8  nn  12n  1 16  nn  1 12  nn  1
 8 3 
2
  n 3  2   n 2  2 
n
6
n
n 
An  
8 12
8n  12n  1 16n  1 12n  1
 8


2
n
2n
n
6n 2
2n 2
An  
8 12
4n  12n  1 8n  1 6n  1
 8


2
n
n
n
3n 2
n2
Acabamos de obtener una fórmula para que, dado el número de rectángulos, se calcule el
área bajo la parábola en el intervalo de [0,2]. Por ejemplo, si suponemos 10 rectángulos,
como en el último caso, se obtiene
A10  
8 12
41121 811 611
 8


 11.12
100 10
300
100
10
que es el mismo resultado. Sin embargo, todo esto se hizo para buscar cual es el área
cuando el número de rectángulos es infinito:
4n  12n  1 8n  1 6n  1
 8 12
A  Limn  2   8 


n
n 
3n 2
n2
 n
resolviendo los límites inmediatos
 4n  12n  1 8n  1 6n  1
A  8  Limn 


n 
3n 2
n2

Después de resolver los productos
 8n 2  12n  4 8n  8 6n  6 
A  8  Limn 



n 
3n 2
n2

se obtienen los límites
A 8
Esta es él área exacta bajo la curva.
8
34
6
3
3