MÓDULO II “RAZONES Y FUNCIONES TRIGONOMÉTRICAS”

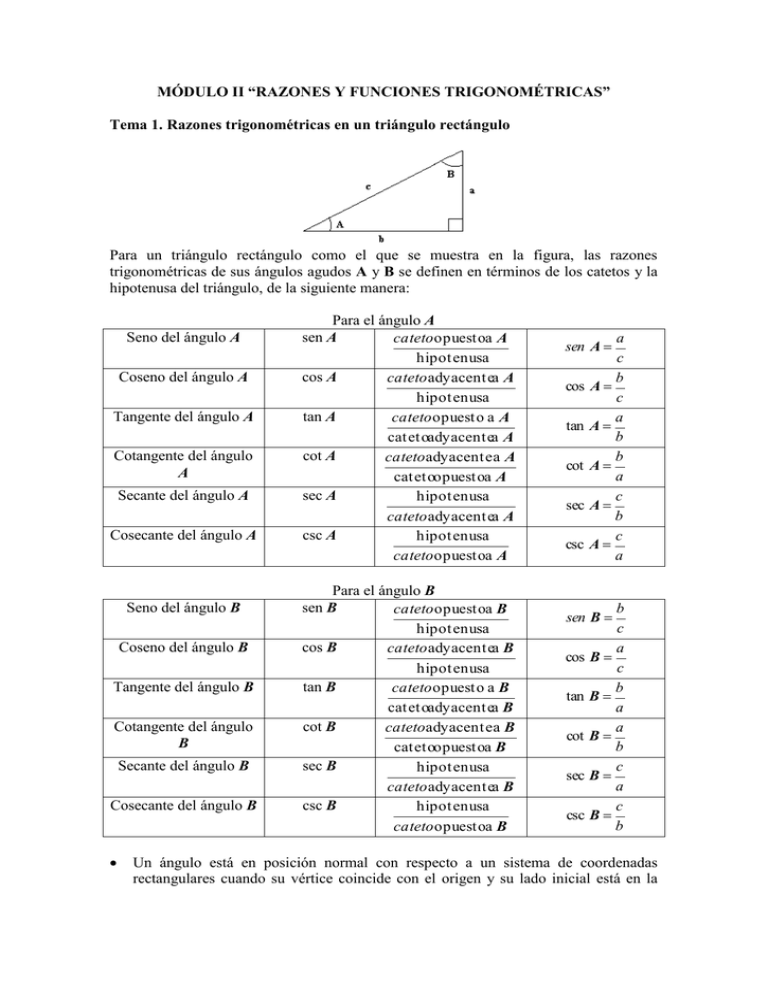
MÓDULO II “RAZONES Y FUNCIONES TRIGONOMÉTRICAS”
Tema 1. Razones trigonométricas en un triángulo rectángulo
Para un triángulo rectángulo como el que se muestra en la figura, las razones
trigonométricas de sus ángulos agudos A y B se definen en términos de los catetos y la
hipotenusa del triángulo, de la siguiente manera:
Seno del ángulo A
Coseno del ángulo A
Tangente del ángulo A
Cotangente del ángulo
A
Secante del ángulo A
Cosecante del ángulo A
Seno del ángulo B
Coseno del ángulo B
Tangente del ángulo B
Cotangente del ángulo
B
Secante del ángulo B
Cosecante del ángulo B

Para el ángulo A
sen A
cateto opuestoa A
hipotenusa
cos A
cateto adyacentea A
hipotenusa
tan A
cateto opuesto a A
catetoadyacentea A
cot A
cateto adyacente a A
catetoopuestoa A
sec A
hipotenusa
cateto adyacentea A
csc A
hipotenusa
cateto opuestoa A
Para el ángulo B
sen B
cateto opuestoa B
hipotenusa
cos B
cateto adyacentea B
hipotenusa
tan B
cateto opuesto a B
catetoadyacentea B
cot B
cateto adyacente a B
catetoopuestoa B
sec B
hipotenusa
cateto adyacentea B
csc B
hipotenusa
cateto opuestoa B
a
c
b
A
c
a
A
b
b
A
a
c
A
b
c
A
a
sen A 
cos
tan
cot
sec
csc
b
c
a
cos B 
c
b
tan B 
a
a
cot B 
b
c
sec B 
a
c
csc B 
b
sen B 
Un ángulo está en posición normal con respecto a un sistema de coordenadas
rectangulares cuando su vértice coincide con el origen y su lado inicial está en la
parte positiva del eje x; el lado final del ángulo puede estar en cualquier cuadrante
del sistema coordenado.

Razones trigonométricas de un ángulo en posición normal.
Si P(x, y) es un punto localizado en cualquier cuadrante de un sistema coordenado
bidimensional, las razones trigonométricas de un ángulo en posición normal cuyo lado
final pasa por el punto P(x, y), se definen en términos de la abscisa de P (x), de la
ordenada de P (y) y del radio vector P (r) de la siguiente manera:
seno del ángulo A
sen A
coseno del ángulo A
cos A
tangente del ángulo A
tan A
cotangente del ángulo
A
cot A
secante del ángulo A
sec A
cosecante del ángulo A
csc A
Ordenada de P
radio vector de P
Abscisa de P
radio vector de P
Ordenada de P
Abscisa de P
Abscisa de P
Ordenada de P
Radio vector de P
Abscisa de P
Radio vector de P
Ordenada de P
y
r
x
cos A 
r
y
tan A 
x
x
cot A 
y
r
sec A 
x
r
csc A 
y
sen A 

Si el lado terminal de un ángulo A en posición normal esta en el primer cuadrante
CI, entonces se dice que A es un ángulo de primer cuadrante (CI)

Si el lado terminal de un ángulo A en posición normal esta en el segundo cuadrante
CII, entonces se dice que A es un ángulo de segundo cuadrante (CII)

Si el lado terminal de un ángulo A en posición normal esta en el tercer cuadrante
CIII, entonces se dice que A es un ángulo de tercer cuadrante (CIII)

Si el lado terminal de un ángulo A en posición normal esta en el cuarto cuadrante
CIV, entonces se dice que A es un ángulo de cuarto cuadrante (CIV)

Si el lado terminal de un ángulo A en posición normal coincide con uno de los ejes
coordenados, entones se dice que A es un ángulo de cuadrante.

Ángulo reducido: El ángulo reducido Ar de un ángulo A, es el ángulo agudo,
positivo, que forma el lado terminal del ángulo A con el eje x. Para ángulos que son
múltiplos pares de 90° su ángulo reducido es 0°; para ángulos que son múltiplos
impares de 90° su ángulo reducido es 90°.

El ángulo reducido Ar de un ángulo A de primer cuadrante es igual a sí mismo, es
decir: Ar = A

El ángulo reducido Ar de un ángulo A de segundo cuadrante es igual a 180° - A, es
decir: Ar = 180° - A

El ángulo reducido Ar de un ángulo A de tercer cuadrante es igual a A – 180°, es
decir: Ar = A – 180°

El ángulo reducido Ar de un ángulo A de cuarto cuadrante es igual a 360° – A, es
decir: Ar = 360° - A
 Problemas.
7. Determina el ángulo reducido de un ángulo de 172° 31’57”
Solución:
El ángulo A = 172° 31’57” se encuentra en el segundo cuadrante, como se muestra en
la siguiente figura:
Por lo tanto el ángulo reducido Ar, del ángulo A = 172° 31’57” es:
Ar = 180° - 172° 31’57”
Ar = 7° 28’ 3’’
8. Obtén el ángulo reducido de un ángulo de 245°
Solución:
El ángulo A = 245° se encuentra en el tercer cuadrante, como se muestra en la siguiente
figura:
Por lo tanto el ángulo reducido Ar, del ángulo A = 245° es:
Ar = 245° - 180°
Ar = 65°
9. Obtén el ángulo reducido de un ángulo de 333° 27’ 54’’
Solución:
El ángulo A = 333° 27’ 54’’ se encuentra en el cuarto cuadrante, como se muestra en la
siguiente figura:
Por lo tanto el ángulo reducido Ar, del ángulo A = 333° 27’ 54’’es:
Ar = 360° - 333° 27’ 54’’°
Ar = 26° 32’ 6’’

Signos de las razones trigonométricas.
SenA  y r
Cos A  x r
Tan A  y x
Cot A  x y
SecA  r x
Csc A  r y
CI
CII
CIII
CIV
+
+
+
+
+
+
+
+
+
+
-
+
+
-
 Problemas.
10. Determina las razones trigonométricas de un ángulo en posición normal cuyo lado
terminal pasa por el punto P(  5, 5 )
Solución:
El ángulo A cuyo lado terminal pasa por el punto P(  5,
segundo cuadrante, como se muestra en la siguiente figura:
5 ) se encuentra en el
La abscisa de P es x   5 ; la ordenada de P es y  5 , y el valor de r se obtiene

  5
2
utilizando el teorema de Pitágoras: r 2   5 
2
 5  5  10
 r  10
Aplicando las definiciones de las razones trigonométricas se tiene que:
sen A =
Ordenada de P
radio vector de P
cos A =
Abscisa de P
radio vector de P
tan A =
Ordenada de P
Abscisa de P
cot A =
Abscisa de P
Ordenada de P
sec A =
csc A =
Radio vector de P
Abscisa de P
Radio vector de P
Ordenada de P
sen A 
5
y
= 
r
10
cos A 
tan A 
cot A 
x  5

r
10
5
y

 1
x  5
 5
x
 1
 
y
5
sec A 
10
r

x  5
csc A 
10
r

y
5
Observa que como el ángulo A se encuentra en el segundo cuadrante, de acuerdo con
los signos de las razones trigonométricas, solamente las razones sen A y csc A son
positivas y todas las demás son negativas.

Determinación de las razones trigonométricas conocida una de ellas.
11. Determina las demás razones trigonométricas del ángulo  si se sabe que
5
sec  
(dos soluciones)
4
Solución:
Como no se especifica el cuadrante en el que se encuentra el ángulo  y sec  tiene
signo negativo, las soluciones estarán en los cuadrantes II y III porque es en estos
cuadrantes donde sec  tiene signo negativo.
Para CII
r 5

, deducimos
x
4
que x = -4 & r = 5 (r es positivo en todos los cuadrantes). Para obtener el valor de y
aplicamos el teorema de Pitágoras:
De acuerdo con la figura anterior y teniendo en cuenta que sec  
 42   y 2  52 ;
y  52  (4)2  25  16  9  3  y  3
Aplicando las definiciones de las razones trigonométricas se tiene que:
y
3
4
x
sen   =
cot   
r
5
3
y
cos  
x 4

r
5
tan  
y
3

x 4
sec  
r
5
5


x 4
4
csc  
r 5

y 3
Observa que como el ángulo  se encuentra en el segundo cuadrante, de acuerdo con
los signos de las razones trigonométricas, solamente las razones sen  y csc  son
positivas y las demás son negativas.
Para CIII
En este caso x = -4; y = -3 & r = 5
Aplicando las definiciones de las razones trigonométricas se tiene que:
y
3
4 4
x
sen   =

cot   
r
5
3 3
y
cos  
x 4

r
5
sec  
r
5
5


x 4
4
5
5
y 3 3
r



csc   
x 4 4
3
y 3
Observa que como el ángulo  se encuentra en el tercer cuadrante, de acuerdo con los
signos de las razones trigonométricas, solamente las razones tan  y cot  son positivas
y las demás son negativas.
tan  
12. Obtén todas las razones trigonométricas si Tan B = –12 / 5 ( Dos soluciones)
y.
y = 12
13
x=5
x = –5
y = –12
13
Como en este problema no se especifica en
que cuadrante se encuentra el ángulo B,
entonces deberemos de considerar los dos
cuadrantes donde la función Tangente es
negativa, siendo estos los cuadrantes II y IV.
Obteniendo en este caso el valor del radio
vector mediante el teorema de Pitágoras
tenemos que
r = (5) 2 122  25  144 169= 13
Por lo tanto r = 13 y las razones
trigonométricas en estos cuadrante son:
II C.
IV C.
Sen B = –12 / 13
Cos B = 5 / 13
Tan B = – 12 / 5
Cot B = – 5 / 12
Sec B = 13 / 5
Csc B = – 13 / 12
Sen B = 12 / 13
Cos B = – 5 / 13
Tan B = – 12 / 5
Cot B = – 5 / 12
Sec B = – 13 / 5
Csc B = 13 / 12

Valores de las razones trigonométricas de cualquier ángulo.
 Problemas.
13. Obtén los valores de las razones trigonométricas de un ángulo de 334° 24’ 42”
utilizando tu calculadora:
Solución:
Cerciórate que tu calculadora este en el modo de grados (deben aparecer en la pantalla
las indicaciones deg o d) Como podrás darte cuenta, en tu calculadora no es posible
obtener directamente los valores de las razones cotangente, secante y cosecante (tu
calculadora no cuenta con estas teclas).Para solucionar este problema, deberás hacer uso
de las siguientes identidades trigonométricas:
cot A 
1
;
tan A
sec A 
1
;
cos A
csc A 
1
senA
Te sugerimos que obtengas los valores de las razones trigonométricas por parejas, es
decir sen A y csc A; cosA y secA & tanA y cot A. Por ejemplo, obtienes el sen A y para
obtener la csc A oprimes la tecla 1/x o bien x-1. Procedes de la misma manera con cosA
y secA & tanA y cot A.
sen 334° 24’ 42” = -0.4319
cos 334° 24’ 42” = 0.9019
tan 334° 24’ 42” = -0.4789
cot 334° 24’ 42” = -2.0882
sec 334° 24’ 42” = 1.1087
csc 334° 24’ 42” = -2.3153
Observa que el ángulo de 334° 24’ 42” está en el cuarto cuadrante y que en este
cuadrante solamente las razones cosA y secA son positivas.
14. Obtén los valores de las razones trigonométricas de un ángulo de - 214°19’39”
Solución:
sen - 214°19’39” = 0.5640
cos - 214°19’39” = -0.8260
tan - 214°19’39” = -0.6829
cot - 214°19’39”= -1.4644
sec - 214°19’39” = -1.2110
csc - 214°19’39” = 1.7733
Observa que el ángulo de - 214°19’39” está en el segundo cuadrante y que en este
cuadrante solamente las razones sen A y csc |A son positivas.

Obtención de un ángulo a partir de una razón trigonométrica
 Problemas.
1. Si csc A = 3.5142, Determine el valor del ángulo A, si 0°  A  360° (dos
soluciones)
Solución:
Para obtener un ángulo cuando se conoce el valor de una de sus razones trigonométricas
es necesario “deshacer” dicha razón trigonométrica. Para tal efecto, debes aplicar la
función trigonométrica inversa correspondiente.
La función inversa de la función senA es sen-1A o bien angsen A.
La función inversa de la función cosA es cos-1A o bien angcos A.
La función inversa de la función tanA es tan-1A o bien angtan A.
Si cotA = x entonces cot-1A o bien angcot A = tan-1(1/x)
Si secA = x entonces sec-1A o bien angsec A = cos-1(1/x)
Si cscA = x entonces csc-1A o bien angcsc A = sen-1(1/x)
Como csc A = 3.5142 es un valor positivo, los ángulos que satisfacen la igualdad
anterior estarán en los cuadrantes CI y CII porque en estos cuadrantes la csc A tiene
signo positivo.
Para “deshacer” la función cosecante en csc A = 3.5142 es necesario aplicar la función
cosecante inversa en ambos miembros de la igualdad anterior, esto es:
csc-1 (csc A) = csc-1 (3.5142)
A = csc-1 (3.5142)
Pero, csc-1 (3.5142) = sen-1(1/3.5142) = 16°31’57.13’’
Por lo tanto, la solución de CI es A = 16°31’57.13’’
Para obtener la solución de CII se considera que 16°31’57.13’’ es el ángulo reducido
del ángulo requerido en CII. Recuerda que en CII, Ar = 180° - A.
En este caso, 16°31’57.13’’ = 180° - A; despejando A de la ecuación anterior:
A = 180° - 16°31’57.13’’ = 163° 28’ 2.87’’
Por lo tanto, la solución de CII es A = 163° 28’ 2.87’’
2. Si cot A = 5.1423, Determine el valor del ángulo A, si 0°  A  360° (dos
soluciones)
Solución:
Como cot A = 5.1423 es un valor positivo, los ángulos que satisfacen la igualdad
anterior estarán en los cuadrantes CI y CIII porque en estos cuadrantes la cot A tiene
signo positivo.
Para “deshacer” la función cotangente en cot A = 5.1423 es necesario aplicar la función
cotangente inversa en ambos miembros de la igualdad anterior, esto es:
cot-1 (cot A) = cot-1 (5.1423)
A = cot-1 (5.1423)
Pero, cot-1 (5.1423) = tan-1(1/5.1423) = 11° 00’ 16.93’’
Por lo tanto, la solución de CI es A = 11° 00’ 16.93’’
Para obtener la solución de CIII se considera que 11° 00’ 16.93’’ es el ángulo reducido
del ángulo requerido en CIII. Recuerda que en CIII, Ar = A – 180°
En este caso, 11° 00’ 16.93’’ = A -180°; despejando A de la ecuación anterior:
A = 180° + 11° 00’ 16.93’’ = 191° 00’ 16.93’’
Por lo tanto, la solución de CIII es A = 191° 00’ 16.93”
Tema 2. Resolución de triángulos

Triángulo rectángulo
Investiga en la bibliografía presentada y contesta las siguientes preguntas:
1. Resuelve el
rectángulo
siguiente
A = 36°20’
triángulo
Solución: Resolver un triángulo significa
encontrar las medidas de sus tres lados y
de sus tres ángulos.
En la figura de la derecha nos falta por
conocer las medidas de los lados b y c y las
magnitudes de los ángulos B y C.
b
c
C
a = 25.72
B
tan A = 25.72/b
Como el triángulo es rectángulo, C = 90°
B = 90° - 36°20’ = 53°40’
36°20’, b= 34.9709
Como conocemos los tres lados y los tres
ángulos, el triángulo está resuelto.
sen A = 25.72/c ; sen 36°20’ = 25.72/c
Despejando c: c= 25.72/sen 36°20’
c= 43.4106
Utilizando el ángulo A
obtenemos los lados b y c.
=
Despejando b: b= 25.72/tan 36°20’
2. Resuelve el
rectángulo.
siguiente
triángulo
C
Solución:
a = 42.42
b = 58.48
En la figura de la derecha nos falta por
conocer la medida del lado c y las
magnitudes de los ángulos A, B y C.
B
Como el triángulo es rectángulo, C = 90°
Para obtener el ángulo A, utilizamos una
razón trigonométrica que relacione su
cateto opuesto con su cateto adyacente, de
esta manera:
tan A = 42.42/58.48; de modo
que:
A = tan-1(42.42/58.48); A = 35°57’22.46’’
c
A
Para obtener el lado c, podemos utilizar al
ángulo A y una razón trigonométrica que
relacione su cateto opuesto con la
hipotenusa, de esta manera:
sen A = 42.42/c; de modo que:
c = 42.42/sen 35°57’22.46’’; c = 72.2452
Como conocemos los tres lados y los tres
ángulos, el triángulo está resuelto.
B = 90° - 35°57’22.46’’ = 54°2’37.54’’

Aplicaciones con triángulos rectángulos.
 Problemas.
1. Calcula el área y perímetro de un triángulo equilátero que mide 5.6 m por lado.
Perímetro: P = 5.6 + 5.6 + 5.6 = 16.8 m
(b)( h)
2
Como el triángulo es equilátero sus tres lados son iguales y sus tres ángulos también,
por lo que cada uno de ellos mide 60°
El área del triángulo está dada por A 
Calculamos la altura del triángulo utilizando una razón trigonométrica de uno de los
ángulos de 60°. Utilizamos razón que relaciona cateto opuesto con hipotenusa:
sen 60° = h/5.6; de modo que:
h = 5.6 sen 60°’; h = 4.8450 m
A
(5.6)(4.84 50)
 13.5660m 2
2
2. Los ángulos interiores de un triángulo isósceles miden 47° 68° y 47°. Sí su área es
30 cm2 determina las longitudes de sus lados
Solución:
De acuerdo con la figura,
(a )( h)
 30 cm 2 , despejando a h: h= 2(30)/a;
2
h= 60/a …….
Por otra parte, tan 47°= h//a/2), despejando a h,
h= (a/2) tan 47° ……
Igualando los segundos miembros de
y
,
60/a = (a/2) tan 47°; 120/ tan 47° = a2
a
120
 10.5784, sustituyendo el valor de a en
tan 47
, h= 60/10.5784, h= 5.6719
Utilizando la razón trigonométrica de uno de los ángulos de 47° que relaciona cateto
opuesto con la hipotenusa, tenemos que:
sen 47°= 5.6719/b, despejando a b de la
(5.6719 )
 7.7553 cm  los lados iguales miden
ecuación anterior tenemos que: b=
sen 47
7.7553cm y el lado diferente 10.5784 cm

Triángulo oblicuángulo.

Al resolver problemas que se modelan a través de triángulos oblicuángulos
podemos identificar cuatro casos diferentes a través de los cuales es posible
abordar dichos problemas. Estos casos son:
I. Cuando se conocen dos ángulos y un lado del triángulo
II. Cuando se conocen dos lados del triángulo y el ángulo opuesto a uno de
ellos
III. Cuando se conocen dos lados del triángulo y el ángulo comprendido entre
ellos
IV. Cuando se conocen los tres lados del triángulo

Los casos I y II del triángulo oblicuángulo se resuelven por medio de la ley
senos, que se expresa simbólicamente de la siguiente manera:
a
b
c


senA senB senC
ó
senA senB senC


a
b
c
Donde a, b y c representan los lados y A, B y C representan los ángulos del triángulo.

Los casos III y IV del triángulo oblicuángulo se resuelven por medio de la ley
cosenos, que se expresa simbólicamente de la siguiente manera:
a 2  b 2  c 2  2bc cos A
b 2  a 2  c 2  2ac cos B
c 2  a 2  b 2  2abcosC
Donde a, b y c representan los lados y A, B y C representan los ángulos del triángulo.

Aplicaciones con triángulos oblicuángulos.
 Problemas.
1. Resuelve el
oblicuángulo.
Solución:
siguiente
triángulo
C
b
a
En la figura de la derecha nos dan como
datos la medida del lado c y las magnitudes
de los ángulos A y B (Caso I: se conocen
A = 35°
c = 25
B = 68°
dos ángulos y un lado del triángulo), razón Para obtener el lado b:
por la cual se utilizara la ley senos.
Obteniendo el ángulo C por diferencia:
b
c
csenB

; despejando b: b 
C = 180° - 35° - 68°= 77°; Ahora:
senB senC
senC
a
c
csenA

; despejando a: a 
senA senC
senC Sustituyendo
25sen68 
b

 23.7893
datos:
Sustituyendo
sen77 
25sen35 
Como conocemos los tres lados y los tres
 14.7166
datos: a 
sen77 
ángulos, el triángulo está resuelto.
2. Resuelve el
oblicuángulo.
Solución:
siguiente
triángulo
C
En la figura de la derecha nos dan como
a = 40.4
datos las medidas de los lados a, b y c
(Caso IV: se conocen los tres lados del
triángulo), razón por la cual se utilizara la
B
c = 62.6
ley cosenos.
Obteniendo el ángulo A:
Obteniendo el ángulo C:
2
2
2
a  b  c  2bc cos A ;
c 2  a 2  b 2  2ab cosC ;
2bc cos A  b 2  c 2  a 2 ;
2ab cosC  a 2  b 2  c 2 ;
b2  c2  a2
cos A 
2bc
 b2  c2  a2
A  cos1 
2bc

Sustituyendo datos:



 a2  b2  c2
C  cos1 
2ab

Sustituyendo datos:



Obteniendo el ángulo B:
b 2  a 2  c 2  2ac cos B ;
2ac cos B  a 2  c 2  b 2 ;
 40.42  30.32  62.62
C  cos1 
2(40.4)(30
.3)

 12359'6.3''



C = 180° - A – B; sustituyendo:
C = 180° - 32°21’9.28’’ -23°39’44.42’’
C = 123°59’6.3”



 40.42  62.62  30.32
B  cos 
2(40.4)(62
.6)

 2339'44.42''
1



Una vez que se han obtenido dos de los
ángulos, es posible obtener el tercero por
diferencia:
Como ejemplo obtendremos nuevamente el
ángulo C de esta manera:
a2  c2  b2
2ac
 a2  c2  b2
B  cos1 
2ac

Sustituyendo datos:
A
a2  b2  c2
cosC 
2ab
 30.32  62.62  40.42
A  cos1 
2(30.3)(62
.6)

 3221'9.28''
cos B 
b = 30.3
Como conocemos los tres lados y los tres
ángulos, el triángulo está resuelto.



3. Para encontrar la distancia entre dos puntos A y B que se encuentran en los
extremos de un lago, un topógrafo elige un punto C que está a 295.m de A y a 480
m de B. Si el ángulo A mide 52° 35’ determine la distancia AB.
Solución:
En la figura de arriba se presenta el esquema que representa al problema. Nos dan como
datos las medidas de los lados a y b, y la magnitudes del ángulo A (Caso II: se conocen
dos lados y el ángulo opuesto a uno de ellos), razón por la cual se utilizara la ley senos.
Obteniendo el ángulo B:
senB senA
 bsenA

, despejando el ángulo B: B  sen1 

b
a
 a 
 295sen5235' 
Sustituyendo datos: B  sen 1 
 ; B= 29°13’2.79’’
480


Obteniendo el ángulo C por diferencia:
C = 180° - A – B; sustituyendo:
C = 180° - 52°35’ -29°13’2.79’’
C = 98°11’57.21”
Ahora, obtenemos el lado c, que es la distancia AB requerida.
c
a
asenC

; despejando el lado c: c 
senC senA
senA
Sustituyendo datos: c 
480sen98 11'57.21' '
;
sen52 35'
c = 598.1753m
4. Un ingeniero civil situado en B observa dos puntos A y C en los extremos de una
laguna. Si BA = 331.7 m, BC = 242.2 m y ABC = 120°41’. Calcula la distancia
AC.
Solución:
En la figura de arriba se presenta el esquema que representa al problema. Nos dan como
datos las medidas de los lados a y c, y la magnitud del ángulo B (Caso III: se conocen
dos lados y el ángulo comprendido entre ellos), razón por la cual se utilizara la ley
cosenos.
Obteniendo el valor del lado b mediante:
b 2  a 2  c 2  2ac cos B , sustituyendo valores:
b  (242.2) 2  (331.7) 2  2(242.2)(331.7) cos12041' ,
b=500.6768 m