Examen de Sistemas Autom´ aticos EPSIG 14 de diciembre de 2005

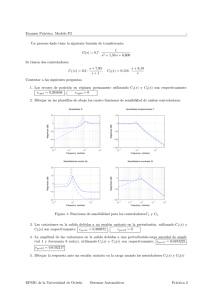
Examen de Sistemas Automáticos
EPSIG
14 de diciembre de 2005
Cuestión. Considérese un sistema de control realimentado unitariamente en el
que
125
(s + 1)
,
G(s) =
C(s) = K
s
(s + 5)3
donde C(s) y G(s) son las funciones de transferencia del controlador y del proceso,
respectivamente. Se pide:
1. Calcular en función de K los errores en régimen permanente de posición, erpp ,
y de velocidad, erpv .
2. Calcular en función de K la variación en la magnitud de salida producida por
una perturbación de carga di (t) de tipo escalón unitario
3. Calcular para K = 1 la amplitud del rizado producido en la variable de salida
cuando la perturbación de carga es
di (t) = cos(2t)
Examen de Sistemas Automáticos
EPSIG
14 de diciembre de 2005
1. El Bell-Boeing V-22 Osprey Tiltrotor es a la vez un helicóptero y un avión. Su principal virtud es la capacidad de girar 90o sus motores hasta una posición vertical para los despegues
y los aterrizajes, y retornarlos a la posición horizontal para navegar como un aeroplano
[1,2]. La relación entre la altitud que toma el aparato, y la fuerza de empuje de los motores
1
puede representarse por G(s) = Fh(s)
= (20s+1)(10s+1)(0,5s+1)
.
m (s)
Figura 1: Bell-Boeing V-22 Osprey Tiltrotor
Se pide:
(a) Analizar el seguimiento de referencias y la capacidad de rechazo de perturbaciones de
entrada de un sistema de control en lazo cerrado de la altitud, que utilice un controlador
2
de la forma C(s) = 280(s +1,5s+0,5)
.
s
(b) Repetir el punto anterior si se añade al sistema un prefiltro entre la referencia y el
0,5
nudo de realimentación con función de transferencia F (s) = s2 +1,5s+0,5
.
Para los dos primeros apartados pueden utilizarse, si se desea, las gráficas de las figuras 2, 3 y
4. En caso de usarlas puede entregarse esta hoja de enunciado para justificar las respuestas.
(c) Un regulador proporciona el ángulo de inclinación de los motores (θtilt ), controlando
v(s)
con ello el avance horizontal del aparato (v), a través de la relación G(s) = θtilt
(s) =
10
= s2 +4,5s+9 .
Diseñar este regulador, de tal forma que ante un cambio de consigna de la velocidad
de la aeronave en forma de escalón, el error de posición sea nulo, la sobreoscilación no
supere un 10 % y el tiempo de establecimiento esté en torno a 10 segundos.
(d) Determinar la ecuación en diferencias del regulador, necesaria para implementar el
sistema de control de manera digital con un microprocesador.
Referencias
[1] A.J. Calise y R.T. Rysdyk, “Nonlinear Adaptive Flight Control Using Neural Networks”,
IEEE Control Systems, Diciembre 1998, pp. 14-23
[2] R.C. Dorf y R.H. Bishop, “Modern Control Systems (tenth edition)”, Pearson Prentice Hall,
2005.
El examen continúa en el reverso de la página.
Página 1 de 2
Examen de Sistemas Automáticos
EPSIG
14 de diciembre de 2005
Diagrama de Bode de C⋅G/(1 + C⋅G) y de F⋅C⋅G/(1 + C⋅G)
100
Magnitude (dB)
50
0
CG/(1+CG)
-50
FCG/(1+CG)
-100
-150
-200
-2
10
-1
0
10
1
10
2
10
10
Frequency (rad/sec)
Respuesta ante escalón unitario de C⋅G/(1 + C⋅G) y de F⋅C⋅G/(1 + C⋅G)
2
CG/(1+CG)
Amplitude
1.5
1
0.5
0
FCG/(1+CG)
10
0
20
30
40
50
60
70
Time (sec)
Figura 2: Diagrama de Bode y respuesta a escalón de
CG
1+CG
y de
F CG
1+CG
Diagrama de Bode de G/(1 + C⋅G) y de G
0
G
Magnitude (dB)
-50
-100
G/(1+CG)
-150
-200
-3
10
-2
-1
10
0
10
1
10
2
10
10
Frequency (rad/sec)
-3
4
x 10
Respuesta ante escalón unitario de G/(1 + C⋅G)
3
Amplitude
2
1
0
-1
-2
0
10
20
30
40
50
60
70
Time (sec)
Figura 3: Diagrama de Bode de
G
1+CG
y de G, y respuesta a escalón de
G
1+CG
Diagrama de Bode de 1/(1 + C⋅G)
50
Magnitude (dB)
0
-50
-100
-150
-3
10
-2
-1
10
0
10
1
10
10
Frequency (rad/sec)
Diagrama de Bode de C/(1+ C⋅G)
100
Magnitude (dB)
80
60
40
20
0
-3
10
-2
10
-1
10
0
10
1
2
10
10
Frequency (rad/sec)
Figura 4: Diagrama de Bode de
1
1+CG
y de
C
1+CG
Fin del examen. No olvidar escribir el nombre y apellidos antes de entregar.
Página 2 de 2