Mapas de Karnaugh

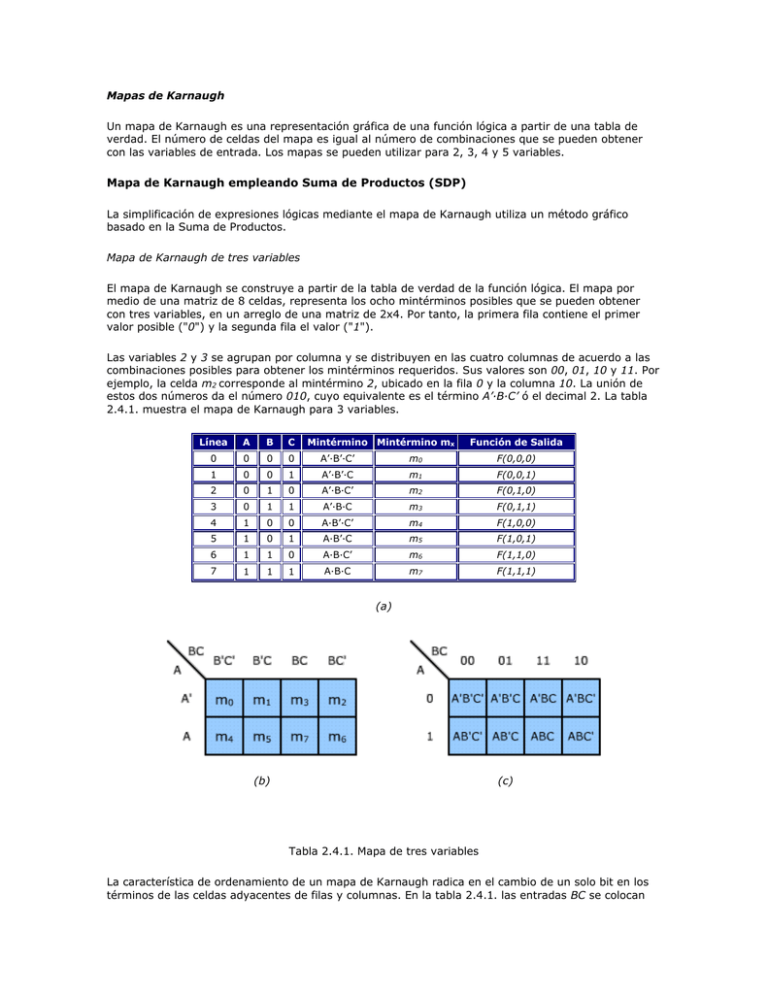
Mapas de Karnaugh
Un mapa de Karnaugh es una representación gráfica de una función lógica a partir de una tabla de
verdad. El número de celdas del mapa es igual al número de combinaciones que se pueden obtener
con las variables de entrada. Los mapas se pueden utilizar para 2, 3, 4 y 5 variables.
Mapa de Karnaugh empleando Suma de Productos (SDP)
La simplificación de expresiones lógicas mediante el mapa de Karnaugh utiliza un método gráfico
basado en la Suma de Productos.
Mapa de Karnaugh de tres variables
El mapa de Karnaugh se construye a partir de la tabla de verdad de la función lógica. El mapa por
medio de una matriz de 8 celdas, representa los ocho mintérminos posibles que se pueden obtener
con tres variables, en un arreglo de una matriz de 2x4. Por tanto, la primera fila contiene el primer
valor posible ("0") y la segunda fila el valor ("1").
Las variables 2 y 3 se agrupan por columna y se distribuyen en las cuatro columnas de acuerdo a las
combinaciones posibles para obtener los mintérminos requeridos. Sus valores son 00, 01, 10 y 11. Por
ejemplo, la celda m2 corresponde al mintérmino 2, ubicado en la fila 0 y la columna 10. La unión de
estos dos números da el número 010, cuyo equivalente es el término A’·B·C’ ó el decimal 2. La tabla
2.4.1. muestra el mapa de Karnaugh para 3 variables.
Línea
A
B
C
Mintérmino Mintérmino mx
Función de Salida
0
0
0
0
A’·B’·C’
m0
F(0,0,0)
1
0
0
1
A’·B’·C
m1
F(0,0,1)
2
0
1
0
A’·B·C’
m2
F(0,1,0)
3
0
1
1
A’·B·C
m3
F(0,1,1)
4
1
0
0
A·B’·C’
m4
F(1,0,0)
5
1
0
1
A·B’·C
m5
F(1,0,1)
6
1
1
0
A·B·C’
m6
F(1,1,0)
7
1
1
1
A·B·C
m7
F(1,1,1)
(a)
(b)
(c)
Tabla 2.4.1. Mapa de tres variables
La característica de ordenamiento de un mapa de Karnaugh radica en el cambio de un solo bit en los
términos de las celdas adyacentes de filas y columnas. En la tabla 2.4.1. las entradas BC se colocan
secuencialmente, cambiando cada vez una sola variable, por eso resulta el orden: 00, 01, 11 y 10. En
la interactividad 2.4.1., la pulsación de cada cuadro activa el mintérmino correspondiente.
Interactividad 2.4.1. Mapa de tres variables
Por ejemplo, la variable C está negada en m4 y m5 no lo está, mientras que A y B no cambia. Las
celdas de los bordes superior e inferior e izquierdo y derecho también cumplen esta condición al
agruparlas unas a otras. En el teorema 12 de la lección 1, se demuestra que la suma de los términos
mínimos en celdas adyacentes pueden ser simplificadas en un término AND de dos literales. Por
consiguiente, aplicando el teorema para los términos m4 y m5 del mapa se tiene:
m4 + m5 = A·B’·C’ + A·B’·C = A·B’·(C’+C) = A·B
Los términos m4 y m6 se pueden asociar de la misma forma:
m4 + m6 = A·B’·C’ + A·B·C’ = A·C’·(B’+B) = A·C’
Ejemplo
Simplificar la función F1= (m3, m4, m5, m6, m7).
F1 = (m3, m4, m5, m6, m7) = A’·B·C + A·B’·C’+ A·B’·C + A·B·C’+ A·B·C
Aplicando el teorema 6 de la lección 1 para el término A·B·C.
F1 = (m3, m4, m5, m6, m7) = (m4, m5, m6, m7) +(m3, m7) = [A·B’·C’+ A·B’·C + A·B·C’+ A·B·C] +
[A’·B·C + A·B·C].
El primer término en la sumatoria es el grupo 1 y el segundo término corrresponde al grupo 2. En un
mapa de karnaugh, los mintérminos de cada grupo se relacionarían a través de lazos independientes.
Desarrollando la expresión,
F1 = [A·B’·(C’+C) + A·B·(C’+ C)] + [B·C·(A’+A)]= A·B’·(1) + A·B·(1) + B·C·(1) = A·(B’+B) + B·C = A
+ B·C.
El mapa se construye colocando un 1 en las celdas correspondientes a los mintérminos presentes en la
función de salida. Por ejemplo, para el término F(1,1,0)= A·B·C’ = 1 se situaría un 1 en la celda 110.
Para los mintérminos no presentes en la función se pone un 0. Por ejemplo el término F(0,0,1)=
A’·B'·C = 0, será una celda con valor 0 en la celda 001.
Después de situar los unos en el mapa, se procede con la agrupación de 1s, la determinación del
término producto correspondiente a cada grupo y la suma de los términos producto obtenidos. La
determinación del término producto se realiza de acuerdo los siguientes criterios:
1.Una celda representa un mintérmino, dando como resultado un término de cuatro literales.
2. Dos celdas agrupadas pueden representar la asociación de dos mintérminos, dando como resultado
un término de dos literales.
3.Cuatro celdas agrupadas pueden representar la asociación de cuatro mintérminos, dando como
resultado un término de un literal.
4. Ocho celdas agrupadas representan un valor de función igual a 1.
Ejemplo
Sea la función del ejemplo anterior, simplificarla por medio del método del mapa.
La tabla de verdad del ejemplo anterior es la siguiente,
Línea
A
B
C
Salida F
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
1
4
1
0
0
1
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
Tabla 2.4.2. Tabla de verdad de la función F1.
El mapa de Karnaugh se configura de acuerdo a los mintérminos iguales a 1 y las celdas se agrupan
tal como en la figura 2.4.1.
Figura 2.4.1. Mapa de Karnaugh de la función F1.
El primer grupo se forma con los mintérminos m4, m5, m6 y m7 y el segundo grupo con los
mintérminos m3 y m7.
Del primer grupo resulta el término A ya que para las cuatro columnas de la tabla existen transiciones
entre las variables B y C. El segundo grupo da como resultado el término BC por el cambio existente
en la variable A.
En total, la función queda reducida a la expresión:
F1 = A + B·C
Mapa de Karnaugh de cuatro variables
La construcción de un mapa de Karnaugh de 4 variables es similar al de 3 variables. La diferencia
radica en el número de variables de entrada. El mapa por medio de una matriz de 16 celdas,
representa los 16 mintérminos posibles (24) que se pueden obtener con cuatro variables de entrada,
en un arreglo de 4 x 4. La disposición de celdas en el mapa se muestra en la tabla 2.4.3.
Línea
A
B
C
D
Mintérmino
Mintérmino mx
Función de Salida
0
0
0
0
0
A’·B’·C’·D’
m0
F(0,0,0,0)
1
0
0
0
1
A’·B’·C’·D
m1
F(0,0,0,1)
2
0
0
1
0
A’·B’·C·D’
m2
F(0,0,1,0)
3
0
0
1
1
A’·B’·C·D
m3
F(0,0,1,1)
4
0
1
0
0
A’·B·C’·D’
m4
F(0,1,0,0)
5
0
1
0
1
A’·B·C’·D
m5
F(0,1,0,1)
6
0
1
1
0
A’·B·C·D’
m6
F(0,1,1,0)
7
0
1
1
1
A’·B·C·D
m7
F(0,1,1,1)
8
1
0
0
0
A·B’·C’·D’
m8
F(1,0,0,0)
9
1
0
0
1
A·B’·C’·D
m9
F(1,0,0,1)
10
1
0
1
0
A·B’·C·D’
m10
F(1,0,1,0)
11
1
0
1
1
A·B’·C·D
m11
F(1,0,1,1)
12
1
1
0
0
A·B·C’·D’
m12
F(1,1,0,0)
13
1
1
0
1
A·B·C’·D
m13
F(1,1,0,1)
14
1
1
1
0
A·B·C·D’
m14
F(1,1,1,0)
15
1
1
1
1
A·B·C·D
m15
F(1,1,1,1)
(a)
(b)
(c)
Tabla 2.4.3. Mapa de cuatro variables
Por ejemplo, la celda m9 corresponde al mintérmino 9, ubicado en la fila 10 y la columna 01. La unión
de estos dos números da el número 1001, cuyo equivalente es el término A·B’·C’·D -ó el decimal 9.
La minimización por medio de un mapa de 4 variables se puede efectuar con las celdas adyacentes
entre sí y las celdas de los bordes que se pueden concatenar para reducir la expresión. Por ejemplo,
m13 y m15 son celdas adyacentes así como m0, m8, m2 y m10.
El mapa se construye colocando un 1 en las celdas correspondientes a los mintérminos presentes en la
función de salida. Por ejemplo, para el término F(1,1,0,0)= A·B·C’·D’ = 1 se situaría un 1 en la celda
1100. Para los mintérminos no presentes en la función se pone un 0. Por ejemplo el término
F(1,1,1,1)= A·B·C·D = 0, será una celda con valor 0 en la celda 1111.
Igual que en el mapa de 3 variables, se procede con la agrupación de 1s, la determinación del término
producto correspondiente a cada grupo y la suma de los términos producto obtenidos.
Las reglas para reducir términos en un mapa de Karnaugh de 4 variables son las siguientes:
1.Una celda representa un mintérmino, dando como resultado un término de cuatro literales.
2. Dos celdas agrupadas pueden representar la asociación de dos mintérminos, dando como resultado
un término de tres literales.
3.Cuatro celdas agrupadas pueden representar la asociación de cuatro mintérminos, dando como
resultado un término de dos literales.
4.Ocho celdas agrupadas pueden representar la asociación de ocho mintérminos, dando como
resultado un término de un literal.
5. Dieciséis celdas agrupadas pueden representan un valor de función igual a 1.
Ejemplo
Simplíquese la función de Boole F2= (m1, m3, m8, m10, m12, m14)
Figura 2.4.2. Mapa de Karnaugh de la función F2.
El primer grupo se forma con los mintérminos m1 y m3 y el segundo grupo se forma con los
mintérminos m8, m10 y m12, m14.
Del primer grupo resulta el término A’·B’·D ya que en la columna 1 no se presentan cambios para las
variables A y B y se presenta transición en la variable C en las columnas 2 y 3. El segundo grupo da
como resultado el término A·D’. La razón radica en la simplificación de la variable B en la tercera y
cuarta fila y en la variable C en la primera y cuarta columna.
Sumando los mintérminos obtenidos se tiene la ecuación simplificada:
F2 = A’·B’·D + A·D’
Mapas de Karnaugh empleando Producto de Sumas (PDS)
La simplificación de expresiones lógicas mediante el mapa de Karnaugh también es posible mediante
el método de producto de sumas. En este método, cada celda representa un maxtérmino.
La construcción del mapa es similar a la suma de productos. La diferencia radica en que cada celda
representa un maxtérmino. Por ejemplo, la celda m2 corresponde al maxtérmino 2, ubicado en la fila 0
y la columna 10. La unión de estos dos números da el número 010, cuyo equivalente es el término
A+B’+C. La figura 2.4.3. muestra el mapa de Karnaugh para 3 variables.
Figura 2.4.3. Mapa de tres variables.
La representación de la función lógica se hace simplemente copiando los ceros de la tabla de verdad
en las celdas del mapa. Este método es más apropiado cuando en la columna de resultados de la tabla
de verdad predominan los ceros.
Ejemplo
Utilizar el mapa de Karnaugh para minimizar el producto de sumas,
F3 = (A+B+C)·(A’+B+C)·(A+B’+C)·(A’+B’+C)
Los maxtérminos se trasladan a cada una de las celdas del mapa de Karnaugh y las celdas se agrupan
tal como en la figura 2.4.4.
Figura 2.4.4. Mapa de Karnaugh de la función F3
El término suma para cada grupo se muestra en la figura y la suma de productos resultante es:
F3 = C
Ejemplo
Utilizar el mapa de Karnaugh para minimizar el producto de sumas,
F4 =
(A+B+C+D)·(A+B’+C)·(A+B’+C’+D’)·(A’+B’+C+D’)·(A’+’B+C’+D’)·(A’+B+C+D’)·(A’+B+C’+D’)·(A’+B'
+C+D’)
El segundo término tiene que ampliarse a (A+B’+C+D)·(A+B’+C+D’). La función completa se pasa al
mapa de karnaugh mostrado en la figura 2.4.5.
Figura 2.4.5. Mapa de Karnaugh de la función F4
El término suma para cada grupo se muestra en la figura 2.4.5. y el producto de sumas resultante es:
F4 = (A+C+D)·(B'+D')·(A'+D')
Condiciones de No Importa
Hasta el momento se ha asumido que la función es igual a 0 en los casos donde la función no es igual
a 1. En algunas aplicaciones esta suposición no es siempre verdadera ya que existen combinaciones
de entrada que no presentan. En un mapa de Karnaugh estas combinaciones de entrada sirven de
herramienta para simplificar la función y su representación se hace por medio de una X en la celda del
mapa. Según la agrupación que convenga se asume un valor de 1 ó 0 para la X con el fin de obtener
la expresión más simple.
Ejemplo
Simplificar la función de Boole F5 =(m0, m4, m7, m9) con condiciones de importa, NI = (m1, m5,
m11, m14).
Los mintérminos se marcan con un 1, las condiciones de no importa con una X y las celdas restantes
con 0.
El mapa de Karnaugh de la función F5 se muestra en la figura 2.4.6.
Figura 2.4.6. Mapa de Karnaugh de la función F5
En suma de productos obtenemos,
F5 = A’·C’·D’ + A'·B’·C’ + A’·B·C·D + A·B'·D
Mapas de Karnaugh.
se
Otra manera de simplificar funciones es representándolas en
mapas de Karnaugh. Esto es equivalente a resolver las
simplificaciones por teoremas. Sin embargo, mucha gente
considera que resulta más fácil visualizar las simplificaciones si
presentan
gráficamente.
Los mapas de Karnaugh pueden aplicarse a dos, tres, cuatro y cinco variables.
Para más variables, la simplificación resulta tan complicada que conviene en ese
caso utilizar teoremas mejor. Para efectos de clase, veremos las simplificaciones
de
dos,
tres
y
cuatro
variables.
Ejemplo 1: Simplifica la función de dos variables f = a'b + ab' + ab
Lo primero que debo de hacer es representarlo en un mapa de dos variables. Se
representa
como
una
tabla.
Para llenar la tabla, pongo un uno donde se intersecte el valor de la función. Por
ejemplo, para el primer término de la función f = a'b + ab' + ab, se ha marcado en
rojo
donde
se
puso
el
1
en
la
tabla.
Una vez hecho el mapa, debemos marcar las regiones contiguas que manejen 1s.
Aquí en el dibujo vemos cómo se marcan dos regiones. Estas regiones son las
simplificaciones. Como la región azul involucra solamente a la b, eso representa.
La región verde, por su parte, involucra solamente a la a. Para cada región,
debemos checar qué variables involucra. En el caso de la región azul, cubre a la b,
pero
con
respecto
a
la
variable a
maneja tanto a
como a', y por eso se descarta la a.
Una vez definidas las regiones, se escribe
la
función
simplificada
f=
b
+
a.
Ejemplo 2: Simplifica la función de tres variables f = a'b + ab'c + c'
Lo primero que debo de hacer es representarlo en un mapa de tres variables. Se
representa
como
se
muestra
en
la
tabla.
Para llenar la tabla, pongo un uno donde se intersecte el valor de la función. Por
ejemplo, para los términos de la función f = a'b +ab'c + c', se ha marcado donde se
puso
el
1
en
la
tabla.
Ahora debemos buscar las regiones que nos indiquen la función simplificada. Lo
primero que debemos observar es que las regiones pueden agruparse de los
extremos del mapa, como la región azul. Esta región representa a c'.
Ahora, vemos que queda un bit en a'bc, pero siempre conviene agruparlo lo más
posible, en regiones cuyas celdas sean múltiplos de 2 (1, 2, 4, 8...) En este caso,
la agrupamos con el 1 contiguo, para que la región quede como a'b.
La región verde se agrupa para formar ab'. Así, la función resultante sería f = a'b +
ab'
+
c.
Ejemplo 3: Simplifica la función de cuatro variables f = ac'd' + a'bd + abcd + ab'cd
+
a'bc'd'
+
a'b'c'd'
Nuevamente, lo primero que hacemos es vaciar la función al mapa. Nótese la
forma
que
toma
el
mapa.
Ahora, lo siguiente es agrupar las variables en regiones. La primer a región, la
roja, está agrupada de las esquinas. Esta agrupación representa a c'. La siguiente
región, la verde la agrupo con el 1 que tiene abajo. Pude haberla agrupado con el
1 a la derecha, pero hubiera significado agrupar un 1 ya agrupado, y dejar otro 1
aún no agrupado sin agrupar. Así que se agrupa de esta forma, y la región verde
representa a a'bd. Los 1s que quedan hasta este momento libre pueden agruparse
juntos,
en
la
región
azul.
Esto
representa
a
acd.
Es importante notar la región naranja. Representa a bcd. Esta región es una
simplificación adicional válida, que pudo haberse manejado. En ocasiones, habrá
varias formas de agrupar a los 1s. Todas son válidas, y representan solcuiones
equivalentes. Sin embargo, hay que cuidar de siempre agrupar las regiones lo más
grandes posibles, y cuidando de agrupar a los 1s de manera que se repitan lo
menos posible.
Ejemplo 3: Simplifica la función de cuatro variables f = ac'd' + a'bd + abcd + ab'cd +
a'bc'd' + a'b'c'd'
Nuevamente, lo primero que hacemos es vaciar la función al mapa. Nótese la forma
que toma el mapa.
Ahora, lo siguiente es agrupar las variables en regiones. La primer a región, la roja,
está agrupada de las esquinas. Esta agrupación representa a c'. La siguiente región,
la verde la agrupo con el 1 que tiene abajo. Pude haberla agrupado con el 1 a la
derecha, pero hubiera significado agrupar un 1 ya agrupado, y dejar otro 1 aún no
agrupado sin agrupar. Así que se agrupa de esta forma, y la región verde representa
a a'bd. Los 1s que quedan hasta este momento libre pueden agruparse juntos, en la
región azul. Esto representa a acd.
Es importante notar la región naranja. Representa a bcd. Esta región es una
simplificación adicional válida, que pudo haberse manejado. En ocasiones, habrá
varias formas de agrupar a los 1s. Todas son válidas, y representan soluciones
equivalentes. Sin embargo, hay que cuidar de siempre agrupar las regiones lo más
grandes posibles, y cuidando de agrupar a los 1s de manera que se repitan lo menos
posible.
Simplificación de funciones con mapas de Karnaugh
Obtener la función de un Mapa de Karnaugh es el procedimiento inverso a la de la realización
del mapa. Un termino de la función coloca uno o mas "unos" en el mapa de Karnaugh.
Tomar esos unos, agrupándolos de la forma adecuada, nos permite obtener los términos de la
función
Utilizaremos los Mapas de Karnaugh para obtener una función mínima de dos niveles Suma de
Productos.
Una expresión de dos niveles sdp se considerará la expresión mínima si:
1. No existe otra expresión equivalente que incluya menos productos.
2. No hay otra expresión equivalente que conste con el mismo numero de productos, pero con
un menor numero de literales.
Observe que hablamos de UNA expresión mínima y lo LA expresión mínima. Esto porque
pueden existir varias expresiones distintas, pero equivalentes, que satisfagan esta definición y
tengan el mismo numero de productos y literales.
La minimización de funciones sobre el mapa de Karnaugh se aprovecha del hecho de que las
casillas del mapa están arregladas de tal forma que entre una casilla y otra, en forma horizontal
o vertical existe ADYACENCIA LOGICA. Esto quiere decir que entre una casilla y otra solo
cambia una variable.
Definimos los mintérminos adyacentes desde el punto de vista lógico como dos mintérminos
que difieren solo en una variable. Agrupando casillas adyacentes obtenemos términos
productos que eliminan las variables que se complementan, resultando esto en una versión
simplificada de la expresión.
El procedimiento es el de agrupar "unos" adyacentes en el mapa; cada grupo corresponderá a
un termino producto, y la expresión final dará un OR (suma) de todos los términos producto. Se
busca obtener el menor numero de términos productos posible, lo que implica que cada termino
producto debe contener el mayor numero de mintérminos posibles.
Antes de comenzar formalmente con la discusión sobre minimización veamos por un momento
el siguiente mapa de Karnaugh, resultado de la función:
_
___ _ _ _ _
_ _ __ _ _ _
_
__
_
__ _ _
_
_
_
AB
f=ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+ABCD+C
D
Como podemos notar, la función está expresada en forma
canónica, por lo que cada mintérmino "colocará" un 1 en su casilla
correspondiente como se muestra en el mapa de Karnaugh
correspondiente.
Supongamos por un momento que agrupemos los "unos" del
mapa de Karnaugh como se muestra en la figura.
Según esto tenemos cuatro términos que son:
termino
I
A
(agrupa 8 unos y es de 1 variable)
_
termino
II
BC
(agrupa 4 unos y es de 2
variables)
_ _
termino
III
AC D
__ _ _
(agrupa 2 unos y es de 3
variables)
(agrupa 1 uno y es de 4
termino IV AB CD
variables)
Puede verse que a medida que agrupamos mayor cantidad de "unos", el termino tiene menos
literales. El agrupamiento se hace con una cantidad de "unos" que son potencias de 2. Así
agrupamos 2 mintérminos, 4 mintérminos y 8 mintérminos. Cada vez que aumentamos, el
termino va eliminando una variable. En una función de 4 variables, un termino que tenga un solo
"uno" tendrá las cuatro variables. De hecho es un termino canónico. Al agrupar dos mintérminos
eliminaremos una variable y el termino quedará de tres variables. Si agrupamos cuatro "unos"
eliminaremos dos variable quedando un termino de dos variables y finalmente si agrupamos
ocho "unos" se eliminaran tres variable para quedar un termino de una variable.
Todo esto se debe a la adyacencia entre casillas y cada vez que agrupamos, se eliminan las
variables que se complementan.
En el ejemplo anterior la función obtenida es:
___ _ _ _ _
f=ABCD+ACD+BC+A
Pero, ¿será esta la función mínima?
Si vemos la figura a la derecha, la forma de agrupar nos da
como resultado:
_ _
f=D+BC+A
que sí es expresión mínima.
Es importante que al "tomar" un uno, se agrupe con todos los
unos adyacentes, aunque estos uno sean parte de otros grupos.
Fíjese que el mintérmino 13 (11002) es común a los tres
términos.
Para simplificar funciones utilizando mapas de Karnaugh hay que tener en cuenta que:




Cada casilla (mintérmino) en un mapa de Karnaugh de n variable tiene n casillas
adyacentes lógicamente, de modo que cada par de casillas defiere en una variable
Al combinar las casillas en un mapa de Karnaugh, agruparemos un número de
mintérminos que sea potencia de dos. Así agrupar dos casillas eliminamos una variable,
al agrupar cuatro casillas eliminamos dos variables, y así sucesivamente. En general, al
agrupar 2n casillas eliminamos n variables.
Debemos agrupar tantas casillas como sea posible; cuanto mayor sea el grupo, el
termino producto resultante tendrá menos literales. Es importante incluir todos los "unos"
adyacentes a un mintérmino que sea igual a uno.
Para que hayan menos términos en la función simplificada, debemos formar el menor
numero de grupos posibles que cubran todas las casillas(mintérminos) que sean iguales
a uno. Un "uno" puede ser utilizado por varios grupos, no importa si los grupos se
solapan. Lo importante es que si un grupo está incluido completamente en otro grupo, o
sus "unos" están cubiertos por otros grupos, no hace falta incluirlo como termino.
Terminología para la simplificación: Implicante, Implicante Primo, Implicante Primo
Esencial.
A continuación definiremos algunos términos comúnmente utilizados en los procesos de
simplificación de funciones lógicas.
Implicante:
Conjunto de unos en un mapa de Karnaugh que representa un termino producto de variables.
Se denomina implicante porque cuando este termino toma el valor 1, implica que también la
función toma el valor 1. Un mintérmino solo es un implicante.
Implicante Primo:
Implicante que no está incluido completamente dentro de otro implicante. No puede combinarse
con otro implicante para eliminar un literal.
Implicante Primo Esencial:
Implicante primo que contiene uno o mas mintérminos que no están incluidos en cualquier otro
implicante primo.
En el siguiente mapa de Karnaugh:
Los términos I II y III son implicantes primos
El termino IV no es implicante primo
Los términos I y III son implicantes primos esenciales
El termino II no es un implicante primo esenciales
La función se obtiene con los términos I y III
Algoritmo de minimización mediante mapas de Karnaugh
1. Identificar los implicantes primos. Para esto se busca obtener los grupos con mayor cantidad
de unos adyacentes. Los grupos deben contener un numero de unos que son potencias de 2.
2.Identificar todos los implicantes primos esenciales
3.La expresión mínima se obtiene seleccionando todos los implicantes primos esenciales y el
menor numero de implicantes primos para cubrir los mintérminos no incluidos en los implicantes
primos esenciales.
Ejemplo: Simplificar la función:
__
_ _
_
_ _
___ _ _
__
_
_
f = A BCD + A B CD+ A BCD+ A BCD + A BCD+ABCD+ABCD+ABCD+ABCD
En los mapas siguientes se muestra el proceso de
simplificación utilizando el algoritmo.
Implicantes primos
Implicantes primos esenciales
_
_ _
_
F(A,B,C,D)=BCD+AD+ACD+BCD
Para practicar puede bajar esta programa freeware muy intuitivo y fácil de usar.
Llenas la tabla de verdad y a medida que vas colocando los unos, se va llenando el
mapa de Karnaugh y se van agrupando los términos. También se pueden marcar los
unos directamente en el mapa de Karnaugh. No se requiere instalación. Ocupa 283
Kb. Haz click en el icono para bajarlo.
Los ejemplos anteriores se realizaron con funciones de 4 variables. Para mapas de Karnaugh
de 5 y 6 variables el procedimiento es esencialmente el mismo solo hay que recordar que un
mintermino es adyacente a otro mintermino que ocupe la misma posición en forma horizontal o
vertical en los cuadrados a los lados del mapa.
Minimización en mapas de Karnaugh de 5 variables
Simplificar la función =
m(0,2,8,11,15,18,20,21,27,28,29,31)
Se coloca un 1 en los minterminos
____
__ _
_
La función quedará f=ACDE+BDE+BCDE+ACD
Minimización en mapas de Karnaugh de 6 variables
Obtenga una función mínima para el siguiente mapa de Karnaugh
pinche aquí para ver la solución
No olvide que después de obtener la función mínima hay que implantar el circuito.
Para los dos ejemplos anteriores obtenga los circuitos respectivos, primero con un
OR de ANDs, y luego utilizando SOLO COMPUERTAS NAND.