Ejercicio nº 1.
Anuncio
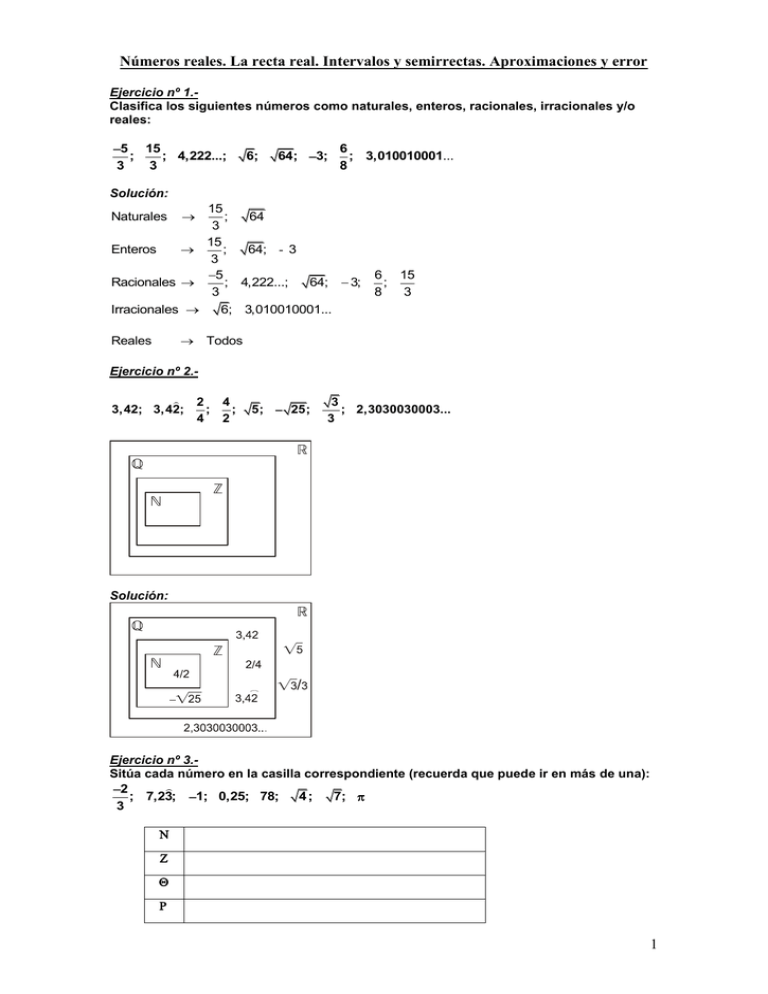
Números reales. La recta real. Intervalos y semirrectas. Aproximaciones y error Ejercicio nº 1.Clasifica los siguientes números como naturales, enteros, racionales, irracionales y/o reales: 5 15 ; ; 4,222...; 3 3 6; 64; 3; 6 ; 3,010010001... 8 Solución: 15 ; 64 3 15 Enteros ; 64; - 3 3 5 Racionales ; 4,222...; 64; 3; 3 Irracionales 6; 3,010010001... Naturales Reales 6 15 ; 8 3 Todos Ejercicio nº 2.3,42; 3,42; 2 4 ; ; 4 2 5; 25; 3 ; 2,3030030003... 3 Solución: Ejercicio nº 3.Sitúa cada número en la casilla correspondiente (recuerda que puede ir en más de una): 2 ; 7,23; 1; 0,25; 78; 4; 7; 3 1 Solución: 78; - 1; 78; 4 2 ; 3 2 ; 3 4 7,23; 1; 0,25; 78; 4 7,23; 1; 0,25; 78; 4; 7; Ejercicio nº 4.Clasifica los siguientes números como naturales, enteros, racionales, irracionales y/o reales: 6 3 16 ; ; ; 25; 5 4 4 Solución: Naturales 25; 7; 20; 36; 5,131131113... 36 16 ; 25; 36; 4 6 3 16 Racionales ; ; : 25; 36; 5 4 4 Irracionales 7; 20; 5,131131113... Enteros Reales Todos Ejercicio nº 5.Escribe en forma de intervalo y representa en cada caso: a) Números comprendidos entre 1 y 4, ambos incluidos. b) Números mayores que 0. c) Números menores que 2 y el propio 2. d) Números comprendidos entre 3 y 4, incluido el 4, pero no el 3. Solución: a) 1, 4 b) 0, c) , 2 d) 3, 4 Ejercicio nº 6.a) Escribe en forma de intervalo y representa: 2 I) , 3 1 II) , 2 3 b) Escribe en forma de intervalo y representa: I) x / 1 x II) x / 3 x 2 Solución: a) I) x / x 3 1 II) x / x 3 2 b) I) 1, II) 3, 2 Ejercicio nº 7.a) Escribe en forma de desigualdad y representa: I) II) 2, 7 4 b) Escribe en forma de intervalo y representa: I) II) x / x / x 3 2 x 0 Solución: a) I) x / 2 x 7 II) x / x 4 3 b) I) - , 3 II) 2, 0 Ejercicio nº 8.a) Escribe en forma de intervalo y representa en cada caso: I) x / 5 x 7 II) x / 2 x b) Escribe en forma de desigualdad y representa: 1 I) , 2 II) 4, 1 Solución: a) I) 5, 7 II) 2, + b) I) x / x 1 2 II) x / 4 x 1 Ejercicio nº 9.Nos dicen que la medida de un campo de forma rectangular es de 45,236 m de largo por 38,54 m de ancho. Sin embargo, no estamos seguros de que las cifras decimales dadas sean correctas. a) Da una aproximación (con un número entero de metros) para las medidas del largo y del ancho del campo. b) Da una cota para el error absoluto y otra para el error relativo cometidos al aproximar de esta forma. Solución: 4 a) Largo 45 m. Ancho 39 m. b) El error absoluto es menor que media unidad del orden de la última cifra significativa: Error absoluto Una cota para el error relativo es: ½ Error relativo½ Valor real Valor aproximado Por tanto: Largo: Error absoluto 0,5 m 0,5 ½ Error relativo½ 0,011 45 Ancho: Error absoluto 0,5 m 0,5 ½ Error relativo½ 0,013 39 Ejercicio nº 10.a) Da una aproximación, con tres cifras significativas, para cada una de las siguientes cantidades: I) 854 238 personas II) 3,1694 m III) 928 412 mg b) ¿Cuáles son los errores absoluto y relativo cometidos en cada caso? Solución: I) 854 238 personas 854 miles de personas Error absoluto Valor real Valor aproximado 854 238 854 000 238 personas Error absoluto 238 Error relativo 0,0003 Valor real 854 238 II) 3,1694 m 3,17 m Error absoluto 3,1694 3,17 0,0006 m 0,0006 Error relativo 0,0002 3,1694 III) 928 412 mg 928 miles de mg Error absoluto 412 mg 412 Error relativo 0,0004 928 412 Ejercicio nº 11.- 5 En una librería se han vendido 5 271 ejemplares de un determinado libro, a 32,45 € cada uno. a) ¿Cuánto dinero se ha recaudado en la venta? Aproxima la cantidad obtenida dando dos cifras significativas. b) Di cuál es el error absoluto y cuál el error relativo cometidos al hacer la aproximación. Solución: a) 5 271 32,45 171 043,95 € 17 decenas de miles de € b) Error absoluto Valor real Valor aproximado 171 043,95 170 000 1 043,95 € Error absoluto 1043,95 Error relativo 0,006 Valor real 171043,95 Ejercicio nº 12.a) Expresa con un número razonable de cifras significativas cada una de las siguientes cantidades: I) Asistentes a un concierto: 25 342 personas. II) Premio que dan en un concurso: 328 053 €. III) Número de libros de cierta biblioteca: 52 243. b) Calcula el error absoluto y el error relativo que se cometen con esas aproximaciones. Solución: I) 25 342 personas 25 miles de personas Error absoluto Valor real - Valor aproximado 25 342 - 25 000 342 personas Error absoluto 342 Error relativo 0,013 Valor real 25342 II) 328 053 € 328 miles de € . Error absoluto 328 053 - 328 000 53 € 53 Error relativo 0,00016 328053 III) 52 243 libros 52 miles de libros Error absoluto 52 243 52 000 243 libros 243 Error relativo 0,0047 52243 6