metodos de ordenamiento java(teoria)

1).Ordenamiento de burbuja
El Ordenamiento de burbuja (Bubble Sort en inglés) es un sencillo algoritmo
de ordenamiento. Funciona revisando cada elemento de la lista que va a ser
ordenada con el siguiente, intercambiándolos de posición si están en el orden
equivocado. Es necesario revisar varias veces toda la lista hasta que no se
necesiten más intercambios, lo cual significa que la lista está ordenada.
Este algoritmo obtiene su nombre de la forma con la que suben por la lista los
elementos durante los intercambios, como si fueran pequeñas "burbujas".
También es conocido como el método del intercambio directo. Dado que solo
usa comparaciones para operar elementos, se lo considera un algoritmo de
comparación, siendo el más sencillo de implementar.
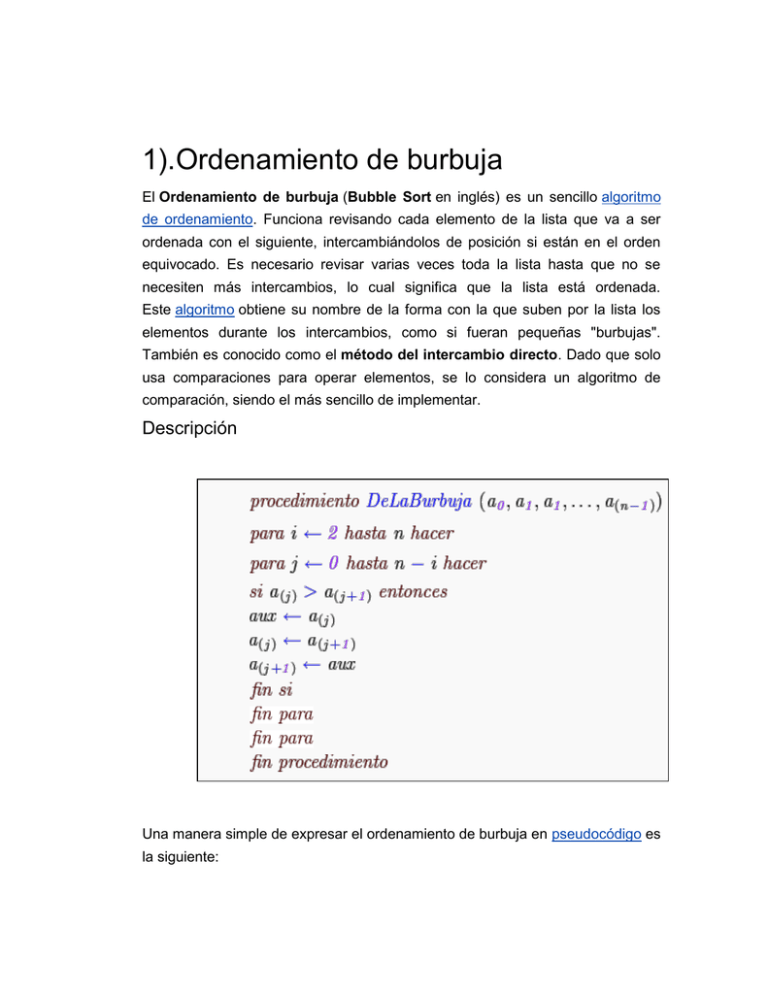
Descripción
Una manera simple de expresar el ordenamiento de burbuja en pseudocódigo es
la siguiente:
Este algoritmo realiza el ordenamiento de una lista a den valores, en este caso
de n términos numerados del 0al n-1, consta de dos bucles anidados uno con el
índicei, que da un tamaño menor al recorrido de la burbuja en sentido inverso
de 2 a n, y un segundo loop con el índice j, con un recorrido desde 0 hasta n-i,
para cada iteración del primer bucle, que indica el lugar de la burbuja.
La burbuja son dos términos de la lista seguidos, j yj+1, que se comparan, si el
primero es menor que el segundo sus valores se intercambian.
Esta comparación se repite en el centro de los dos bucles, dando lugar a la
postre a una lista ordenada, puede verse que el número de repeticiones sola
depende de n, y no del orden de los términos, esto es si pasamos al algoritmo
una lista ya ordenada, realizara todas las comparaciones exactamente igual que
para una lista no ordenada, esta es una característica de este algoritmo, luego
verano una variante que evita este inconveniente.
Para comprender el funcionamiento, veamos un ejemplo sencillo:
Tenemos una lista de números que hay que ordenar:
Podemos ver que la lista que tiene cinco términos,
luego:
El índice i hará un recorrido de 2 hasta n:
Que en este caso será de 2 a 5. Para cada
uno de los valores de i, j tomara sucesivamente los valores
de 0 hasta n-i:
Para cada valor de j, obtenido en ese orden, se compara el
valor del índice j con el siguiente:
Si el termino j es menor, en su caso podría se mayor,
q
u
e
e
l
t
e
r
mino j+1, los valores se permutan, en caso contrario se
continúa con la iteración.
Para el caso del ejemplo, tenemos que:
Para la primera iteración del primer bucle:
y j tomara los valores de 0 hasta 3:
Cuando j vale 0, se comparan
, el 55 y el 86, dado que 55 < 86 no se
permutan el orden.
Ahora j vale 1 y se comparan
el 86 y el 48 Como 86 > 48, se permutan,
dando lugar a una nueva lista.
Se repite el proceso hasta que j valga 3, dando lugar a una re lista super
ordenada, podemos ver que el termino de mayor valor esta en el lugar más alto.
Ahora i vale 3, y j hará un recorrido de 0 a 2.
Primero j vale 0, se comparan
, el 55 y el 48, como 55 > 48 se permutan
dando lugar a la nueva lista.
Para j = 1 se compara el 55 con el 16 y se cambian de orden.
Para j = 2 se compara el 55 y el 82 y se dejan como están, finalizando el bucle
con una lista mejor ordenada, puede verse que los dos valores más altos ya
ocupan su lugar. No se ha realizado ninguna comparación con el termino cuarto,
dado que ya se sabe que después del primer ciclo es el mayor de la lista.
El
algoritmo
consiste
en
comparaciones
sucesivas
de
dos
términos
consecutivos, ascendiendo de abajo a arriba en cada iteración, como la
ascensión de las burbujas de aire en el agua, de ahí el nombre del
procedimiento, en la primera iteración el recorrido ha sido completo, en el
segundo se ha dejado él último termino, al tener ya el mayor de los valores, en
los sucesivos sé ira dejando re realizar las ultimas comparaciones, como se
puede ver.
Ahora
ya i vale
4
y j recor
rerá los
valores
de 0 a
1.
Cuando j vale 0, se comparan
esto es el 48 y el 16 dado que 48 es mayor
que 16 se permutan los valores, dando lugar a una lista algo más ordenada que
la anterior, desde esta nueva ordenación, j pasa a valer 1, con lo que se
comparan los términos
el 48 y el 55 que quedan en el mismo orden.
En este caso la burbuja ha ascendido menos que en los casos anteriores, y la
lista esta ya ordenada, pero el algoritmo tendrá que completarse, realizando una
ultima iteración.
Hay que tener en cuenta que el bucle para realiza un número fijo de repeticiones
y para finalizar tendrán que completarse, aun en el caso extremo, de que la lista
estaría previamente ordenada.
Por último i vale
5 y j solo puede
vale 0, con lo que
solo se realizara
una comparación
de
el 16 y
el 48, que ya
están ordenados
y se dejan igual.
Los
bucles
finalizan y también el procedimiento, dejando la lista ordenada.
Una variante que finaliza en caso de que la lista este ordenada, puede ser la
siguiente, empleando un centinela ordenado, que detecta que no se ha
modificado la lista en un recorrido de la burbuja, y que por tanto la lista ya esta
ordenada, finalizando.
2). Ordenamiento por inserción
El ordenamiento por inserción (insertion sort en inglés) es una manera muy natural de
ordenar para un ser humano, y puede usarse fácilmente para ordenar un mazo de cartas
numeradas en forma arbitraria. Requiere O(n²) operaciones para ordenar una lista de n
elementos.
Inicialmente se tiene un solo elemento, que obviamente es un conjunto ordenado. Después,
cuando hay k elementos ordenados de menor a mayor, se toma el elemento k+1 y se
compara con todos los elementos ya ordenados, deteniéndose cuando se encuentra un
elemento menor (todos los elementos mayores han sido desplazados una posición a la
derecha). En este punto se inserta el elemento k+1 debiendo desplazarse los demás
elementos.
Ejemplo de funcionamiento
En el siguiente ejemplo, 32 debe ser insertado entre 26 y 47, y por lo tanto 47, 59 y 96 deben
ser desplazados.
k+1
11 26 47 59 96 32
11 26
47 59 96
11 26 32 47 59 96
En la implementación computacional, el elemento k+1 va comparándose de atrás para
adelante, deteniéndose con el primer elemento menor. Simultáneamente se van haciendo
los desplazamientos.
11
11
11
11
11
26
26
26
26
26
47 59 96
47 59
47
59
47 59
32 47 59
32
96
96
96
96
El algoritmo en pseudocódigo (con listas que empiezan por 0) debería ser como el siguiente:
algoritmo insertSort( A : lista de elementos ordenables )
para i=1 hasta longitud(A) hacer
index=A[i]
j=i-1
mientras j>=0 y A[j]>index hacer
A[j+1] = A[j]
j = j - 1
fin mientras
A[j+1] = index
fin para
fin algoritmo
Aunque este algoritmo tiene un mejor orden de complejidad que el de burbuja, es muy
ineficiente al compararlo con otros algoritmos comoquicksort. Sin embargo, para listas
relativamente pequeñas el orden por inserción es una buena elección, no sólo porque puede
ser más rápido para cantidades pequeñas de elementos sino particularmente debido a su
facilidad de programación.
Java
public static void insertSort (int[] v) {
for (int i=1; i<v.length; i++) {
int aux = v[i];
int j;
for (j=i-1; j>=0 && v[j]>aux; j--)
v[j+1] = v[j];
v[j+1] = aux;
}
}
3).Ordenamiento Shell
El ordenamiento Shell (Shell sort en inglés) es un algoritmo de ordenamiento. El método
se denomina Shell en honor de su inventorDonald Shell. Su implementación original,
requiere O(n2) comparaciones e intercambios en el peor caso. Un cambio menor presentado
en el libro de V. Pratt produce una implementación con un rendimiento de O(nlog2 n) en el
peor caso. Esto es mejor que las O(n2) comparaciones requeridas por algoritmos simples
pero peor que el óptimo O(n log n). Aunque es fácil desarrollar un sentido intuitivo de cómo
funciona este algoritmo, es muy difícil analizar su tiempo de ejecución.
El Shell sort es una generalización del ordenamiento por inserción, teniendo en cuenta dos
observaciones:
1. El ordenamiento por inserción es eficiente si la entrada está "casi ordenada".
2. El ordenamiento por inserción es ineficiente, en general, porque mueve los valores
sólo una posición cada vez.
El algoritmo Shell sort mejora el ordenamiento por inserción comparando elementos
separados por un espacio de varias posiciones. Esto permite que un elemento haga "pasos
más grandes" hacia su posición esperada. Los pasos múltiples sobre los datos se hacen con
tamaños de espacio cada vez más pequeños. El último paso del Shell sort es un simple
ordenamiento por inserción, pero para entonces, ya está garantizado que los datos del
vector están casi ordenados.
Ejemplo
Considere un pequeño valor que está inicialmente almacenado en el final del vector. Usando
un ordenamiento O(n2) como el ordenamiento de burbuja o el ordenamiento por inserción,
tomará aproximadamente n comparaciones e intercambios para mover este valor hacia el
otro extremo del vector. El Shell sort primero mueve los valores usando tamaños de espacio
gigantes, de manera que un valor pequeño se moverá bastantes posiciones hacia su
posición final, con sólo unas pocas comparaciones e intercambios.
Uno puede visualizar el algoritmo Shell sort de la siguiente manera: coloque la lista en una
tabla y ordene las columnas (usando unordenamiento por inserción). Repita este proceso,
cada vez con un número menor de columnas más largas. Al final, la tabla tiene sólo una
columna. Mientras que transformar la lista en una tabla hace más fácil visualizarlo, el
algoritmo propiamente hace su ordenamiento en contexto (incrementando el índice por el
tamaño de paso, esto es usando i += tamaño_de_paso en vez de i++).
Por ejemplo, considere una lista de números como [ 13 14 94 33 82 25 59 94 65
23 45 27 73 25 39 10 ]. Si comenzamos con un tamaño de paso de 5, podríamos
visualizar esto dividiendo la lista de números en una tabla con 5 columnas. Esto quedaría
así:
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10
Entonces ordenamos cada columna, lo que nos da
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45
Cuando lo leemos de nuevo como una única lista de números, obtenemos [ 10 14 73 25
23 13 27 94 33 39 25 59 94 65 82 45 ]. Aquí, el 10 que estaba en el extremo
final, se ha movido hasta el extremo inicial. Esta lista es entonces de nuevo ordenada
usando un ordenamiento con un espacio de 3 posiciones, y después un ordenamiento con
un espacio de 1 posición (ordenamiento por inserción simple).
El Shell sort lleva este nombre en honor a su inventor, Donald Shell, que lo publicó en 1959.
Algunos libros de texto y referencias antiguas le llaman ordenación "Shell-Metzner" por
Marlene Metzner Norton, pero según Metzner, "No tengo nada que ver con el algoritmo de
ordenamiento, y mi nombre nunca debe adjuntarse a éste." [1]
[editar]Secuencia
de espacios
La secuencia de espacios es una parte integral del algoritmo Shell sort. Cualquier secuencia
incremental funcionaría siempre que el último elemento sea 1. El algoritmo comienza
realizando un ordenamiento por inserción con espacio, siendo el espacio el primer número
en la secuencia de espacios. Continua para realizar un ordenamiento por inserción con
espacio para cada número en la secuencia, hasta que termina con un espacio de 1. Cuando
el espacio es 1, el ordenamiento por inserción con espacio es simplemente un ordenamiento
por inserción ordinario, garantizando que la lista final estará ordenada.
La secuencia de espacios que fue originalmente sugerida por Donald Shell debía comenzar
con N /
2 y dividir por la mitad el número hasta alcanzar 1. Aunque esta secuencia
proporciona mejoras de rendimiento significativas sobre los algoritmos cuadráticos como
el ordenamiento por inserción, se puede cambiar ligeramente para disminuir más el tiempo
necesario medio y el del peor caso. El libro de texto de Weiss demuestra que esta secuencia
permite un ordenamiento O(n2) del peor caso, si los datos están inicialmente en el vector
como (pequeño_1, grande_1, pequeño_2, grande_2, ...) - es decir, la mitad alta de los
números están situados, de forma ordenada, en las posiciones con índice par y la mitad baja
de los números están situados de la misma manera en las posiciones con índice impar.
Quizás la propiedad más crucial del Shell sort es que los elementos permanecen kordenados incluso mientras el espacio disminuye. Se dice que un vector dividido en k
subvectores esta k-ordenado si cada uno de esos subvectores esta ordenado en caso de
considerarlo aislado. Por ejemplo, si una lista fue 5-ordenada y después 3-ordenada, la lista
está ahora no sólo 3-ordenada, sino tanto 5-ordenada como 3-ordenada. Si esto no fuera
cierto, el algoritmo desharía el trabajo que había hecho en iteraciones previas, y no
conseguiría un tiempo de ejecución tan bajo.
Dependiendo de la elección de la secuencia de espacios, Shell sort tiene un tiempo de
ejecución en el peor caso de O(n2) (usando los incrementos de Shell que comienzan con 1/2
O(n3 / 2) (usando los incrementos de
Hibbard de 2k − 1), O(n4 / 3) (usando los incrementos de Sedgewick de 9(4i) − 9(2i) + 1,
o 4i + 1 + 3(2i) + 1), o O(nlog2n), y posiblemente mejores tiempos de ejecución no
del tamaño del vector y se dividen por 2 cada vez),
comprobados. La existencia de una implementación
O(nlogn) en el peor caso del Shell sort
permanece como una pregunta por resolver.
[editar]Implementaciones
El Shell sort se usa comúnmente en lenguajes de programación; esto es una implementación
del algoritmo en C/C++ para ordenar un vectorde enteros. La secuencia de incrementos
usada en este ejemplo de código da un tiempo de ejecución O(n2) en el peor caso.
Java
public static void shellSort(int[] a) {
for ( int increment = a.length / 2;
increment > 0;
increment = (increment == 2 ? 1 : (int)
Math.round(increment / 2.2))) {
for (int i = increment; i < a.length; i++) {
for (int j = i; j >= increment && a[j - increment] >
a[j]; j -= increment) {
int temp = a[j];
a[j] = a[j - increment];
a[j - increment] = temp;
}
}
}
}
4). Quicksort
El ordenamiento rápido (quicksort en inglés) es un algoritmo basado en la técnica
de divide y vencerás, que permite, en promedio, ordenar n elementos en un tiempo
proporcional a n log n.
Descripción del algoritmo
El algoritmo consta de los siguientes pasos:

Elegir un elemento de la lista de elementos a ordenar, al que llamaremos pivote.

Resituar los demás elementos de la lista a cada lado del pivote, de manera que a un
lado queden todos los menores que él, y al otro los mayores. Los elementos iguales al
pivote pueden ser colocados tanto a su derecha como a su izquierda, dependiendo de la
implementación deseada. En este momento, el pivote ocupa exactamente el lugar que le
corresponderá en la lista ordenada.

La lista queda separada en dos sublistas, una formada por los elementos a la
izquierda del pivote, y otra por los elementos a su derecha.

Repetir este proceso de forma recursiva para cada sublista mientras éstas
contengan más de un elemento. Una vez terminado este proceso todos los elementos
estarán ordenados.
Como se puede suponer, la eficiencia del algoritmo depende de la posición en la que termine
el pivote elegido.

En el mejor caso, el pivote termina en el centro de la lista, dividiéndola en dos
sublistas de igual tamaño. En este caso, el orden de complejidad del algoritmo
es O(n·log n).

En el peor caso, el pivote termina en un extremo de la lista. El orden de complejidad
del algoritmo es entonces de O(n²). El peor caso dependerá de la implementación del
algoritmo, aunque habitualmente ocurre en listas que se encuentran ordenadas, o casi
ordenadas. Pero principalmente depende del pivote, si por ejemplo el algoritmo
implementado toma como pivote siempre el primer elemento del array, y el array que le
pasamos está ordenado, siempre va a generar a su izquierda un array vacío, lo que es
ineficiente.

En el caso promedio, el orden es O(n·log n).
No es extraño, pues, que la mayoría de optimizaciones que se aplican al algoritmo se
centren en la elección del pivote.
[editar]Demostración
Podríamos probar el orden de ejecución en el mejor caso de la siguiente manera:
Vamos a suponer que el número total de elementos a ordenar es potencia de dos, es
decir, n = 2k. de aquí podemos ver que k = log2(n), donde k es el número de divisiones que
realizará el algoritmo.
En la primera fase del algoritmo habrán n comparaciones, en la segunda fase el algoritmo
creará dos sublistas aproximadamente de tamaño n/2. El número total de comparaciones de
estas dos sublistas es: 2(n/2) = n. En la tercera fase el algoritmo procesará 4 sublistas más,
por tanto el número total de comparaciones en esta fase es 4(n/4) = n.
En conclusión, el número total de comparaciones que hace el algoritmo es:
n + n + n + ..... + n = kn, donde k = log2(n), por tanto el tiempo de ejecución del algoritmo en el
mejor caso es O(n.log2n)
[editar]Optimización
del algoritmo
Cabe destacar que de usarse en su versión recursiva las siguientes optimizaciones y sus
desventajas no se ven vistas en el tiempo de ejecución del mismo manteniéndose, así el
tiempo de ejecución planteado en un principio.
[editar]Técnicas
de elección del pivote
El algoritmo básico del metodo Quicksort consiste en tomar cualquier elemento de la lista al
cual denominaremos como pivote, dependiendo de la partición en que se elija, el algoritmo
será más o menos eficiente.

Tomar un elemento cualquiera como pivote tiene la ventaja de no requerir ningún
cálculo adicional, lo cual lo hace bastante rápido. Sin embargo, esta elección «a ciegas»
siempre provoca que el algoritmo tenga un orden de O(n²) para ciertas permutaciones de
los elementos en la lista.

Otra opción puede ser recorrer la lista para saber de antemano qué elemento
ocupará la posición central de la lista, para elegirlo como pivote. Esto puede hacerse
en O(n) y asegura que hasta en el peor de los casos, el algoritmo sea O(n·log n). No
obstante, el cálculo adicional rebaja bastante la eficiencia del algoritmo en el caso
promedio.

La opción a medio camino es tomar tres elementos de la lista - por ejemplo, el
primero, el segundo, y el último - y compararlos, eligiendo el valor del medio como
pivote.
[editar]Técnicas
de reposicionamiento
Una idea preliminar para ubicar el pivote en su posición final sería contar la cantidad de
elementos menores que él, y colocarlo un lugar más arriba, moviendo luego todos esos
elementos menores que él a su izquierda, para que pueda aplicarse la recursividad.
Existe, no obstante, un procedimiento mucho más efectivo. Se utilizan dos índices: i, al que
llamaremos índice izquierdo, y j, al que llamaremos índice derecho. El algoritmo es el
siguiente:

Recorrer la lista simultáneamente con i y j: por la izquierda con i (desde el primer
elemento), y por la derecha con j (desde el último elemento).

Cuando lista[i] sea mayor que el pivote y lista[j] sea menor, se intercambian los
elementos en esas posiciones.

Repetir esto hasta que se crucen los índices.

El punto en que se cruzan los índices es la posición adecuada para colocar el pivote,
porque sabemos que a un lado los elementos son todos menores y al otro son todos
mayores (o habrían sido intercambiados).
[editar]Transición
a otro algoritmo
Como se comentó antes, el algoritmo quicksort ofrece un orden de ejecución O(n²) para
ciertas permutaciones "críticas" de los elementos de la lista, que siempre surgen cuando se
elige el pivote «a ciegas». La permutación concreta depende del pivote elegido, pero suele
corresponder a secuencias ordenadas. Se tiene que la probabilidad de encontrarse con una
de estas secuencias es inversamente proporcional a su tamaño.

Los últimos pases de quicksort son numerosos y ordenan cantidades pequeña de
elementos. Un porcentaje medianamente alto de ellos estarán dispuestos de una
manera similar al peor caso del algoritmo, volviendo a éste ineficiente. Una solución a
este problema consiste en ordenar las secuencias pequeñas usando otro algoritmo.
Habitualmente se aplica el algoritmo de inserción para secuencias de tamaño menores
de 8-15 elementos.

Pese a que en secuencias largas de elementos la probabilidad de hallarse con una
configuración de elementos "crítica" es muy baja, esto no evita que sigan apareciendo (a
veces, de manera intencionada). El algoritmo introsort es una extensión del algoritmo
quicksort que resuelve este problema utilizando heapsort en vez de quicksort cuando el
número de recursiones excede al esperado.

Parámetros:

Se debe llamar a la función Quicksort desde donde quiera ejecutarse

Ésta llamará a colocar pivote para encontrar el valor del mismo

Se ejecutará el algoritmo Quicksort de forma recursiva a ambos lados del
pivote
int colocar(int *v, int b, int t)
{
int i;
int pivote, valor_pivote;
int temp;
pivote = b;
valor_pivote = v[pivote];
for (i=b+1; i<=t; i++){
if (v[i] < valor_pivote){
pivote++;
temp=v[i];
v[i]=v[pivote];
v[pivote]=temp;
}
}
temp=v[b];
v[b]=v[pivote];
v[pivote]=temp;
return pivote;
}
void Quicksort(int* v, int b, int t)
{
int pivote;
if(b < t){
pivote=colocar(v, b, t);
Quicksort(v, b, pivote-1);
Quicksort(v, pivote+1, t);
}
}
Nota: Los tres parámetros de la llamada inicial a Quicksort serán array[0], 0,
numero_elementos -1, es decir, si es un array de 6 elementos array[0], 0, 5
[editar]Ejemplo
En el siguiente ejemplo se marcan el pivote y los índices i y j con las letras p, i y j
respectivamente.
Comenzamos con la lista completa. El elemento pivote será el 4:
5 - 3 - 7 - 6 - 2 - 1 - 4
p
Comparamos con el 5 por la izquierda y el 1 por la derecha.
5 - 3 - 7 - 6 - 2 - 1 - 4
i
j
p
5 es mayor que 4 y 1 es menor. Intercambiamos:
1 - 3 - 7 - 6 - 2 - 5 - 4
i
j
p
Avanzamos por la izquierda y la derecha:
1 - 3 - 7 - 6 - 2 - 5 - 4
i
j
p
3 es menor que 4: avanzamos por la izquierda. 2 es menor que 4: nos mantenemos ahí.
1 - 3 - 7 - 6 - 2 - 5 - 4
i
j
p
7 es mayor que 4 y 2 es menor: intercambiamos.
1 - 3 - 2 - 6 - 7 - 5 - 4
i
j
p
Avanzamos por ambos lados:
1 - 3 - 2 - 6 - 7 - 5 - 4
iyj
p
En este momento termina el ciclo principal, porque los índices se cruzaron. Ahora
intercambiamos lista[i] con lista[sup] (pasos 16-18):
1 - 3 - 2 - 4 - 7 - 5 - 6
p
Aplicamos recursivamente a la sublista de la izquierda (índices 0 - 2). Tenemos lo siguiente:
1 - 3 - 2
1 es menor que 2: avanzamos por la izquierda. 3 es mayor: avanzamos por la derecha.
Como se intercambiaron los índices termina el ciclo. Se intercambia lista[i] con lista[sup]:
1 - 2 - 3
El mismo procedimiento se aplicará a la otra sublista. Al finalizar y unir todas las sublistas
queda la lista inicial ordenada en forma ascendente.
1 - 2 - 3 - 4 - 5 - 6 - 7
[editar]Implementaciones
El algoritmo de ordenamiento rápido (Quicksort) en:
Pseudocódigo
function quicksort(array)
var list, less, greater
if length(array) ≤ 1
return array
seleccionar y eliminar un valor pivote pivot en el array
for each x in array
if x < pivot then añadir x a less
else añadir x a greater
return concadenar(quicksort(less), pivot, quicksort(greater))
Java
//Recibe un vector de enteros y el índice del primer y último
elemento válido del mismo
void ordenarQuicksort(int[] vector, int primero, int ultimo){
int i=primero, j=ultimo;
int pivote=vector[(primero + ultimo) / 2];
int auxiliar;
do{
while(vector[i]<pivote) i++;
while(vector[j]>pivote) j--;
if (i<=j){
auxiliar=vector[j];
vector[j]=vector[i];
vector[i]=auxiliar;
i++;
j--;
}
} while (i<=j);
if(primero<j) ordenarQuicksort(vector,primero, j);
if(ultimo>i) ordenarQuicksort(vector,i, ultimo);
}
5).Ordenamiento por selección
El ordenamiento por selección (Selection Sort en inglés) es un algoritmo de
ordenamiento que requiere O(n2)operaciones para ordenar una lista de n elementos.
Su funcionamiento es el siguiente:

Buscar el mínimo elemento de la lista

Intercambiarlo con el primero

Buscar el mínimo en el resto de la lista

Intercambiarlo con el segundo
Y en general:

Buscar el mínimo elemento entre una posición i y el final de la lista

Intercambiar el mínimo con el elemento de la posición i
De esta manera se puede escribir el siguiente pseudocódigo para ordenar una lista
de n elementos indexados desde el 1:
para i=1 hasta n-1
minimo = i;
para j=i+1 hasta n
si lista[j] < lista[minimo] entonces
minimo = j /* (!) */
fin si
fin para
intercambiar(lista[i], lista[minimo])
fin para
Este algoritmo mejora ligeramente el algoritmo de la burbuja. En el caso de tener que
ordenar un vector de enteros, esta mejora no es muy sustancial, pero cuando hay que
ordenar un vector de estructuras más complejas, la operación intercambiar() sería más
costosa en este caso. Este algoritmo realiza muchas menos operaciones intercambiar() que
el de la burbuja, por lo que lo mejora en algo. Si la línea comentada con (!) se sustituyera
por intercambiar(lista[i], lista[j]) tendríamos una versión del algoritmo de la burbuja
(naturalmente eliminando el orden intercambiar del final).
Otra desventaja de este algoritmo respecto a otros como el de burbuja o de inserción directa
es que no mejora su rendimiento cuando los datos ya están ordenados o parcialmente
ordenados. Así como, por ejemplo, en el caso de la ordenación de burbuja se requeriría una
única pasada para detectar que el vector ya está ordenado y finalizar, en la ordenación por
selección se realizarían el mismo número de pasadas independientemente de si los datos
están ordenados o no.
[editar]Implementaciones

Java
void selecccion(int[] a)
{
for (int i = 0; i < a.length - 1; i++)
{
int min = i;
for (int j = i + 1; j < a.length; j++)
{
if (a[j] < a[min])
{
min = j;
}
}
if (i != min)
{
int aux= a[i];
a[i] = a[min];
a[min] = aux;
}
}
}
6). Ordenamiento por mezcla
El algoritmo de ordenamiento por mezcla (merge sort en inglés) es un algoritmo de
ordenamiento externo estable basado en la técnicadivide y vencerás. Es
de complejidad O(n log n).
Descripción
Fue desarrollado en 1945 por John Von Neumann.
Conceptualmente, el ordenamiento por mezcla funciona de la siguiente manera:
1. Si la longitud de la lista es 0 ó 1, entonces ya está ordenada. En otro caso:
2. Dividir la lista desordenada en dos sublistas de aproximadamente la mitad del
tamaño.
3. Ordenar cada sublista recursivamente aplicando el ordenamiento por mezcla.
4. Mezclar las dos sublistas en una sola lista ordenada.
El ordenamiento por mezcla incorpora dos ideas principales para mejorar su tiempo de
ejecución:
1. Una lista pequeña necesitará menos pasos para ordenarse que una lista grande.
2. Se necesitan menos pasos para construir una lista ordenada a partir de dos listas
también ordenadas, que a partir de dos listas desordenadas. Por ejemplo, sólo será
necesario entrelazar cada lista una vez que están ordenadas.
A continuación se describe el algoritmo en pseudocódigo (se advierte de que no se incluyen
casos especiales para vectores vacíos, etc.; una implementación en un lenguaje de
programación real debería tener en cuenta estos detalles):
function mergesort(array A[x..y])
begin
if (x-y > 1)):
array A1 := mergesort(A[x..(int( x+y / 2))])
array A2 := mergesort(A[int(1+(x+y / 2))..y])
return merge(A1, A2)
else:
return A
end
function merge(array A1[0..n1], array A2[0..n2])
begin
integer p1 := 0
integer p2 := 0
array R[0..(n1 + n2 + 2)]//suponiendo que n1 y n2 son las
posiciones
//del array y no el length de este mismo, de otro modo seria (n1 +
n2)
while (p1 <= n1 or p2 <= n2):
if (p1 <= n1 and A1[p1] <= A2[p2]):
R[p1 + p2] := A1[p1]
p1 := p1 + 1
else
if (p2 <= n2 and A1[p1] > A2[p2]):
R[p1 + p2] := A2[p2]
p2 := p2 + 1
return R
end
[editar]Implementaciones
Java
public class MergeSort{
private int A[];
public int[] OrdenaMerge(int[] L) {
int n = L.length;
if (n >
int
int
int
1){
m = (int) (Math.ceil(n/2.0));
[] L1 = new int[m];
[] L2 = new int[n-m];
for (int i = 0; i < m; i++){
L1[i] = L[i];
}
for (int i = m; i < n; i++){
L2[i-m] = L[i];
}
L = merge(OrdenaMerge(L1), OrdenaMerge(L2));
}
return L;
}
public int[] eliminar(int [] l){
int [] L = new int[l.length-1];
for(int i = 1; i < l.length; i++){
L[i-1] = l[i];
}
return L;
}
public int[] merge(int[] L1, int[] L2) {
int[] L = new int[L1.length+L2.length];
int i = 0;
while ((L1.length != 0) && (L2.length != 0)) {
if (L1[0] < L2[0]){
L[i++] = L1[0];
L1 = eliminar(L1);
if (L1.length == 0){
while (L2.length != 0) {
L[i++] = L2[0];
L2 = eliminar(L2);
}
}
}
else{
L[i++] = L2[0];
L2 = eliminar(L2);
if (L2.length == 0) {
while (L1.length != 0) {
L[i++] = L1[0];
L1 = eliminar(L1);
}
}
}
}
return L;
}
public void generarNumeros(){
Random ran = new Random();
int x;
for(int i = 0; i < A.length; i++){
x = (int)(ran.nextDouble()*10000);
A[i] = x;
}
}
public void imprimir(){
for(int i = 0; i < A.length; i++){
System.out.println(A[i]);
}
}
public int[] getA(){
return A;
}
public void setA(int []A){
this.A = A;
}
}