Otros problemas

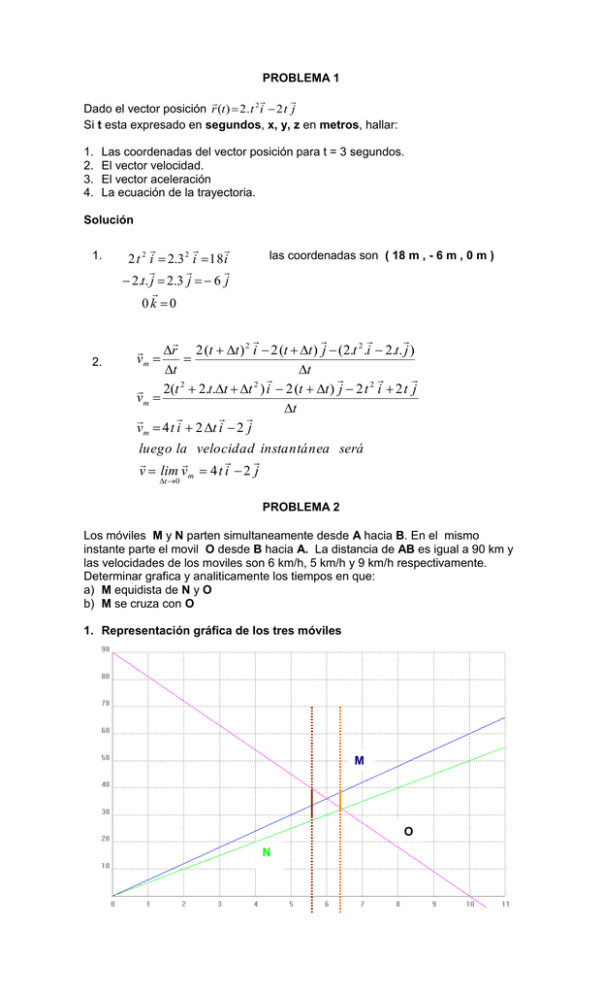
PROBLEMA 1



Dado el vector posición r (t )  2 . t 2 i  2 t j
Si t esta expresado en segundos, x, y, z en metros, hallar:
1.
2.
3.
4.
Las coordenadas del vector posición para t = 3 segundos.
El vector velocidad.
El vector aceleración
La ecuación de la trayectoria.
Solución
1.
2.



2 t 2 i  2.3 2 i  18 i



 2.t. j  2.3 j   6 j

0k 0
las coordenadas son ( 18 m , - 6 m , 0 m )





 r 2 (t  t ) 2 i  2 (t  t ) j  (2.t 2 .i  2.t. j )
vm 

t
t




 2(t 2  2.t.t  t 2 ) i  2 (t  t ) j  2 t 2 i  2 t j
vm 
t




v m  4 t i  2 t i  2 j
luego la velocidad instantánea será




v  lim v m  4 t i  2 j
t 0
PROBLEMA 2
Los móviles M y N parten simultaneamente desde A hacia B. En el mismo
instante parte el movil O desde B hacia A. La distancia de AB es igual a 90 km y
las velocidades de los moviles son 6 km/h, 5 km/h y 9 km/h respectivamente.
Determinar grafica y analiticamente los tiempos en que:
a) M equidista de N y O
b) M se cruza con O
1. Representación gráfica de los tres móviles
M
O
N
2. Resolución analítica
a)
X M  6.t ;
X N  5.t
X O  90 9.t
;
Debe cumplirse que:
X N  X M  XO  X M
5.t  6.t  90  9.t  6.t
 t  90 15.t
como  t  t
y
t t
para t  0
y
t  t para
t0
t  90  15.t
luego
 t  90  15.t
luego
b) X  6.t
y
90
 5,625  5h37 '
16
90
t
 6,43  6h25'
14
t
X  90  9.t
90
6.t  90  9.t  t 
 6h
15
igualando nos queda que:
PROBLEMA 3
Del origen de coordenadas parte un móvil siguiendo el eje y a una velocidad de 6
km/h , simultaneamente otro siguiendo el eje x a una velocidad de 8 km/h. Al cabo
de 10 horas, los móviles dan vuelta y marchan hacia el origen de las coordenadas,
pero ahora la velocidad del primero es la que tenía el segundo y la del segundo la
que tenía el primero. ¿Cuántas veces y en qué instantes estarán separados entre
si por 35 km?
Ida
X  6.t
X  8.t
Ecuación horaria del Móvil y:
Ecuación horaria del Móvil x:
Aplicando el teorema de Pitágoras :
2
km
 km   km 
(35 ) 2   6 .t    8 .t 
h
 h   h 
2
despejado t  3,5  3h30'
Vuelta
Ecuación horaria del Móvil y:
Ecuación horaria del Móvil x:
km
 8.t
h
km
X  10 h.8
.  6.t
h
X  10 h.6
Aplicando el teorema de Pitágoras :
2
2
(35) 2  60  8.t   80  6.t 
352  602  2.60.8.t  8.t 2  802  2.80.6.t  (6.t ) 2
resolviendo 100t 2  1920.t  8775 0
t  7,5  7h30'
luego contando el tiempo desde que partieron será: t f  10h  7h30'  17h30'
PROBLEMA 4
0
S
1m
2m
El mando de aceleración electrónico de un
tren maqueta está programado para que la
velocidad varíe en función de la posición
del modo que se representa. Hallar el
tiempo que tarda el tren en dar una vuelta
completa.
Nota: El gráfico de la velocidad respecto
de la posición corresponde exactamente a
una vuelta completa que realiza el tren en
el circuito.
1m
m
v[ ]
s
0,250
0,125
0
2 + /2
2
2+
4+
4 + 3/2 
4 + 2
/2
Distancia s en m
Figura de Cálculo:
4
3
2
5
Tramos 0- 1 y 3- 4 corresponden a MRU.
Tramos 1- 2 y 4- 5 corresponden a MRUV
(El tren desacelera)
Tramos 2- 3 y 5- 0 corresponden a MRUV
(El tren acelera)
0
1
Analizamos el tramo 0 - 1:
X 1  X 0  V0 t1  t0 
2  0  0,25t1  0
↔
↔
X0 = 0; X1 = 2 [m]; t0 = 0; V0 = V1 = 0,25 [m/s]
↔
2
t1 
↔
↔
t1  8s
t10  t43  8s
0,25
Analizamos el tramo 1- 2:
A
X 2  X 1  V1 t 2  t1  
1
2
a1 t 2  t1 
2

1

2
 2    2  0,25t21   a * t21 
2
2

V2  V1  a1 t2  t1 
0,125
a
II
t21
↔
Reemplazando II en I resulta:
↔
↔
X2 = 2+π/2 [m]; a1 = -a

2
 0,25t21  
1
2
a * t21 
2
↔
I
V2 = 0,125 [m/s]; ↔ 0,125 0,25  at21  ↔

1   0,125
t21 2
 0,25t21   * 
2
2  t21 

 0,25t21   0,0625 t21 
↔
2
t21  t54  8,38s B
↔

2

2
 0,25t21   0,0625 t21  ↔
 0,1875 t 21 
↔ t21 

2 * 0,1875
Analizamos el tramo 2 - 3:
X 3  X 2  V2 t3  t2  
1
2
a 2 t3  t 2 
2
2      2     0,125t32   1 a * t32 2
2
2

V3  V2  a2 t3  t2 
0,125
a
IV
t32
↔
↔
↔
V3 = 0,25 [m/s];
X3 = 2+π [m]; a2 = a ↔

2
 0,125t32  
1
2
a * t32 
2
↔ 0,25  0,125 at32  ↔
Reemplazando IV en III resulta:

 0,125t32  
1  0,125
t32 2 ↔
* 
2  t32 
2

 0,125t32   0,0625 t32 
2
t32  t05  8,38s C
↔

2

2
 0,125t32   0,0625 t32 
↔
 0,1875 t32 

↔ t32 
2 * 0,1875
Sumando todos los intervalos obtenemos el tiempo total transcurrido cuando el
tren da una vuelta completa (Vuelve al origen)
ttotal  t10  t21  t32  t43  t54  t05 ↔ ttotal  8  8,38  8,38  8  8,38  8,38
ttotal  49,52s
PROBLEMA 5
B
A
Un Hombre provisto de un arco lanza una flecha hacia un blanco, con una
velocidad inicial de 10 m/s. La flecha, desacelera por efecto del rozamiento
con el aire a razón de 2 m/s². A los 3 segundos, quien lanzó la flecha
escucha el sonido del impacto de la misma sobre el blanco. Sabiendo que la
velocidad del sonido en el aire es de 336 m/s aproximadamente, ¿A que
distancia del Arquero se encuentra dicho blanco?
Figura de cálculo:
III
x0 = 0
t0 = 0
v0 = 10 m/s
a0 = -2 m/s²
x1 =
t1 =
v1 =
El tramo 10 se realiza con
MRUV (la flecha desacelera
por efecto del rozamiento con
el aire) mientras que el tramo
32 se realiza con MRU siendo
la velocidad de propagación
del sonido constante. Además
sabemos que ΔX32 = -ΔX10 I
x3 = x0 = 0
x2 = x1
t3= 3 s
t2 = t 1
v2 = -336
v2 = -336
m/s
m/s
Analizando el tramo 1- 0 (MRUV) obtenemos que:
1
1
2
2
X 1  X 0  V0 t1  t0   * a * t1  t0 
X 1  X 0  10t1  t0    2 t1  t0 
↔
2
2
2
↔
X 10  10t1  t12
X 10  10t1  0  t1  0
II
Analizando el tramo 3 - 2 (MRU) obtenemos que:
↔ X 32  3363  t2  ↔ t2 = t1; ↔ X 32  3363  t1 
X 3  X 2  V2 * t3  t2 
Reemplazando I en III resulta:
↔
 X 10  3363  t1 
X 10  3363  t1  IV
Finalmente igualando II y IV obtenemos:
↔
10t1  t12  3363  t1 
10t1  t12  1008 336t1
↔
 b  b 2  4ac
346  3462  4 * 1 * 1008
↔
2a
2
346 340,12
346  119716 4032
346 115684
↔
↔
↔ t1 = 2,94[s]
2
2
2
t12  346t1  1008 0
↔
Reemplazo t1 en IV y obtengo:
X 10  3363  t1 
↔
X 10  3363  2,94 ↔
X  20,16m
PROBLEMA 6
240 m
Superman vuela al nivel de los árboles cuando ve que el elevador de la Torre Eiffel
empieza a desplomarse (el cable se rompe). Su visión de rayos x le indica que
Luisa Lane está en el interior. Si Superman se encuentra a 1 km de distancia de la
torre, y el elevador cae desde una altura de 240 m (sobre los árboles), ¿cuánto
tarda Superman en salvar a Luisa y cuál debe ser su velocidad media?
1000 m
Figura de cálculo:
III
[y+]
y1=240
y0=0
[x+]
x1=1000
x0=0
v1=cte.
El elevador cae tal que:
1
2
Y0  Y1  V1 t1  t 0   a t1  t 0 
2
 240  4,9t1 
2
↔
t1 
↔ 0  240  0t1  0 
240
4,9
↔
1
 9,8t1  02 ↔
2
t1  7s
Para Superman la Vm
Vm10 
X 10
t10
↔
Vm 10 
X1  X 0
t1  t0
↔
1000  0
70
Vm 10 
↔
Vm10  142,86m / s
1,20 m
15 m
PROBLEMA 7
¿Te acordás del Angel Malvado?...bueno... pues Tomas (el ángel malvado) y su
primo Mark están parados en un puente que está 15m sobre la carretera, sujetan
un muñeco que piensan lanzar en el momento preciso para que caiga sobre un
automóvil que viaja en línea recta sin acelerar. Si lanzan el muñeco con una
velocidad de 6,4 m/s y el automóvil viaja a 50Km/h. ¿Dónde debe estar el auto
cuando lanzan el muñeco? Tené en cuenta que el parabrisas del vehículo (que es
donde debe caer el muñeco) se encuentra a 1,20 m del piso
Figura de cálculo:
[y+]
yo=15m
y1=1,2m
x0=0
x1=?
[x+]
v1=50 km/h
El muñeco caerá tal que:
1
2
Y1  Y0  V1 y t1  t 0   at1  t 0 
2
 13,8  6,4t1   4,9t1 
2
↔ 1,2  15  6,4t1  0 
1
 9,8t1  02 ↔
2
 b  b 2  4ac
↔ 4,9t  6,4t1  13,8  0 ↔
↔
2a
2
1
 6,4  6,4 2  4(4,9)13,8
↔ (Desprecio la solución negativa) ↔ t1  1,15s
2a
Por otro lado, el auto se desplaza con MRU tal que:
m 

1000 
km 
km  13,89 m y además ↔ X  X  V t  t  ↔ entonces:
VA  50
*
1
0
0 1
0

h  3600 s 
s
h 

X1  16m
X 1  0  13,891,15  t0  ↔
3.






v 4(t  t ) i  2 j  (4 t i  2 j )
am 

t
t


am  4 i
4.
x  2t2 t 
y   2t
reem plazando
y2
x
2
x
2