PROBLEMAS DE TERMODINÁMICA Y FÍSICA ESTADÍSTICA I HOJA 4

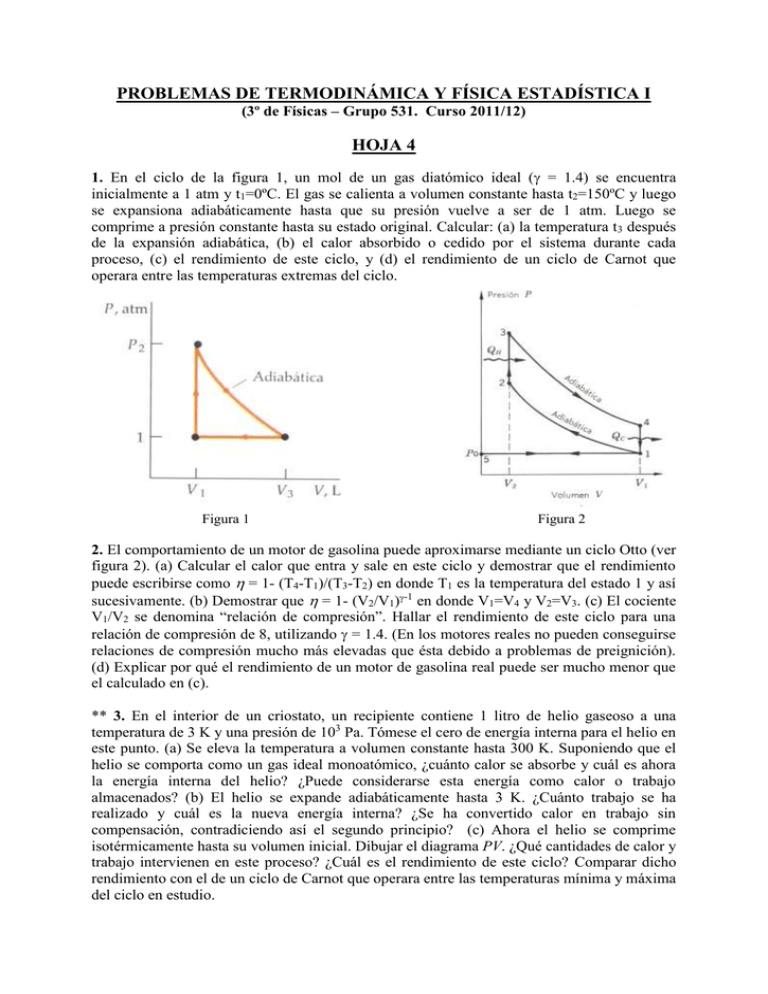
PROBLEMAS DE TERMODINÁMICA Y FÍSICA ESTADÍSTICA I
(3º de Físicas – Grupo 531. Curso 2011/12)
HOJA 4
1. En el ciclo de la figura 1, un mol de un gas diatómico ideal ( = 1.4) se encuentra
inicialmente a 1 atm y t1=0ºC. El gas se calienta a volumen constante hasta t2=150ºC y luego
se expansiona adiabáticamente hasta que su presión vuelve a ser de 1 atm. Luego se
comprime a presión constante hasta su estado original. Calcular: (a) la temperatura t3 después
de la expansión adiabática, (b) el calor absorbido o cedido por el sistema durante cada
proceso, (c) el rendimiento de este ciclo, y (d) el rendimiento de un ciclo de Carnot que
operara entre las temperaturas extremas del ciclo.
Figura 1
Figura 2
2. El comportamiento de un motor de gasolina puede aproximarse mediante un ciclo Otto (ver
figura 2). (a) Calcular el calor que entra y sale en este ciclo y demostrar que el rendimiento
puede escribirse como  = 1- (T4-T1)/(T3-T2) en donde T1 es la temperatura del estado 1 y así
sucesivamente. (b) Demostrar que  = 1- (V2/V1)-1 en donde V1=V4 y V2=V3. (c) El cociente
V1/V2 se denomina “relación de compresión”. Hallar el rendimiento de este ciclo para una
relación de compresión de 8, utilizando  = 1.4. (En los motores reales no pueden conseguirse
relaciones de compresión mucho más elevadas que ésta debido a problemas de preignición).
(d) Explicar por qué el rendimiento de un motor de gasolina real puede ser mucho menor que
el calculado en (c).
** 3. En el interior de un criostato, un recipiente contiene 1 litro de helio gaseoso a una
temperatura de 3 K y una presión de 103 Pa. Tómese el cero de energía interna para el helio en
este punto. (a) Se eleva la temperatura a volumen constante hasta 300 K. Suponiendo que el
helio se comporta como un gas ideal monoatómico, ¿cuánto calor se absorbe y cuál es ahora
la energía interna del helio? ¿Puede considerarse esta energía como calor o trabajo
almacenados? (b) El helio se expande adiabáticamente hasta 3 K. ¿Cuánto trabajo se ha
realizado y cuál es la nueva energía interna? ¿Se ha convertido calor en trabajo sin
compensación, contradiciendo así el segundo principio? (c) Ahora el helio se comprime
isotérmicamente hasta su volumen inicial. Dibujar el diagrama PV. ¿Qué cantidades de calor y
trabajo intervienen en este proceso? ¿Cuál es el rendimiento de este ciclo? Comparar dicho
rendimiento con el de un ciclo de Carnot que operara entre las temperaturas mínima y máxima
del ciclo en estudio.
4. (a) Obtener una expresión para el rendimiento térmico de un ciclo Diesel ideal en función
de la constante adiabática del gas  y de los cocientes rC y rE, donde el cociente rC =V1/V2 se
denomina “relación de compresión” y el cociente rE =V3/V2 se denomina “relación de
expansión” para un motor diesel. La relación de compresión de un motor diesel es mucho
mayor que el de uno de gasolina porque no hay preignición ya que sólo se comprime aire.
(b) Suponer que rC =20, rE =5 y  = 1.4, y calcular el rendimiento térmico.
5. Una máquina de Carnot absorbe 100 J de calor de un foco térmico a la temperatura del
punto de ebullición normal del agua y cede calor a un foco térmico a la temperatura del punto
triple del agua. Encontrar el calor cedido, el trabajo realizado por la máquina y el rendimiento
térmico de ésta.
6. El estado inicial de 0.1 moles de un gas ideal monoatómico es P0 = 32 Pa y V0 = 8 m3. El
estado final es P1 = 1 Pa y V1 = 64 m3. Supóngase que el gas experimenta un proceso a lo
largo de la línea recta que une estos dos puntos y cuya ecuación es P = aV + b, siendo
a = 31/56 y b = 255/7. Dibujar esta línea en un diagrama PV. Calcular:
(a) T en función de V a lo largo de esta línea.
(b) El valor de V para el cual T es máxima.
(c) Los valores de T0, Tmax y T1.
(d) El calor Q transferido al pasar del volumen V0 a cualquier otro volumen V sobre esta línea.
(e) El valor de V y P para los cuales Q es máximo.
(f) El calor transferido a lo largo de la línea al pasar de V0 a V(Q=Qmax).
(g) El calor transferido al pasar de V(Q=Qmax) a V1.
** 7. Demostrar que los estados inicial y final del problema anterior se encuentran situados
sobre una adiabática. Haciendo el recorrido de 0 a 1 por la línea del problema anterior y
regresando de 1 a 0 a lo largo de la adiabática se describe un ciclo que Willis y Kirwin, de la
Universidad de Rhode Island, denominaron “Sadly Cannot”. Dibujar, a escala, el diagrama
PV de este ciclo y calcular:
(a) El trabajo realizado sobre el gas durante la adiabática.
(b) El trabajo neto realizado durante el ciclo.
(c) El calor total transferido al gas desde el entorno.
(d) El rendimiento del ciclo.
(e) El rendimiento de un ciclo de Carnot funcionando entre dos fuentes de calor a las
temperaturas máxima y mínima del ciclo dado.
** Estos problemas tienen doble puntuación.
*La calidad y claridad de la presentación de los problemas vale un punto.