Ejercicios complementarios cálculo

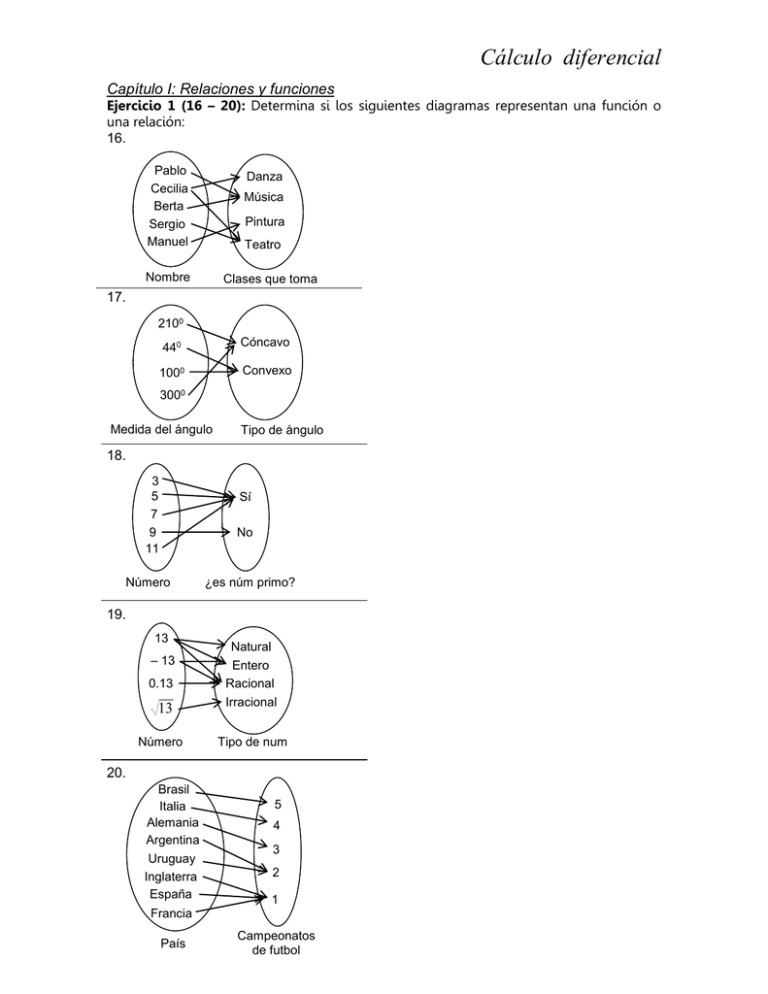
Cálculo diferencial
Capítulo I: Relaciones y funciones
Ejercicio 1 (16 – 20): Determina si los siguientes diagramas representan una función o
una relación:
16.
Pablo
Cecilia
Berta
Sergio
Manuel
Danza
Música
Pintura
Teatro
Nombre
Clases que toma
17.
2100
440
Cóncavo
1000
Convexo
3000
Medida del ángulo
Tipo de ángulo
18.
3
5
7
9
11
Sí
No
Número
¿es núm primo?
19.
13
– 13
0.13
13
Número
Natural
Entero
Racional
Irracional
Tipo de num
20.
Brasil
Italia
Alemania
Argentina
Uruguay
Inglaterra
España
5
4
3
2
1
Francia
País
Campeonatos
de futbol
Ejercicio 2 (6 – 8): Evalúa las siguientes funciones:
f ( x  h)  f ( x )
h
f ( x  h)
f (7 ) ,
f ( x)
6.
Si
f ( x )  x 3 , determina f (2) ,
7.
Si
f ( x)  2 x , determina
Si
x2
2
, determina f (0) , f (6) , f x 
f ( x) 
x6
8.
Ejercicio 3 (27 – 30): Determina el dominio de las siguientes funciones:
27. f ( x)  2  x2
1
28. f ( x)  2  x3
1
29. f ( x)  2  x 
1
30. f ( x)  2  x 
 12
Ejercicio 4 (1 – 28): Obtén la gráfica de las siguientes funciones:
1. f ( x)  4
2. f ( x)  6
3. f (x)  
4. f ( x)  e
5. f ( x)  3x  5
6. f ( x)  2 x
7.
8.
9.
1
x 1
2
3
f ( x)   x  2
4
2
f ( x)  x  4 x  3
f ( x) 
10. f ( x)  x 2  8 x  9
11. f ( x)  2 x 2  12 x
12. f ( x)  4  x 2
3
x7
2
f ( x)  
x 5
4
f ( x)  2
x  6x
1
f ( x)   2
x  3 x  28
f ( x)  x  8
13. f ( x) 
14.
15.
16.
17.
18. f ( x)  9  x
19. f ( x) 
x 2  3x  40
20. f ( x)  9  x 2
21. f ( x) 
1
x 1
2
22. f ( x)  x 2  8 x  9
3
x7
24. f ( x)   6
23. f ( x) 
25. f ( x)  2(3) x
26. f ( x)  8(0.5) x
27. f ( x)  (0.9) x
28. f ( x)  5(2) x
Ejercicio 4 (29 – 40): Relaciona cada función con su gráfica correspondiente (las gráficas
están representadas por las letras A, B, C, D, E, F, G, H, I, J, K y L:
35. f ( x)  2 x  9
( ____ )
36. f ( x)  3x  x  10
( ____ )
( ____ )
37. f ( x) 
( ____ )
31. f ( x)  x  36
( ____ )
38. f ( x)  (3)
32. f ( x)  4(0.8)
( ____ )
39. f ( x)  
5
x2
30. f ( x)   23 x  4
( ____ )
29. f ( x) 
2
x
33. f ( x)   x  7 x  13 ( ____ )
2
34. f ( x)  1  x 2
A.
( ____ )
2
x7
x
9
x4
40. f ( x)  x  2
( ____ )
( ____ )
( ____ )
B.
C.
D.
E.
F.
G.
H.
I.
J.
K.
L.
Ejercicio 6 (1 – 20): Describe los desplazamientos y / o reflexiones de las gráficas básicas
necesarios para obtener la gráfica de las siguientes funciones:
1. y  x 2  3
2.
y  x 2  2 x  15
3.
y   x 2  8x  16
y   x2  3
y  ( x  4)3
4.
5.
6.
7.
y   x3
y  (  x) 3
y  ( x  1)3  20
1
5
9. y 
x4
 1 
10. y  

 x 3
11. y  x  2
8.
12. y   x  4
13. y 
 x 1
14. y    x
15. y  x  6
16. y   x  3
17. y  2  x
18. y  0.5x3
19. y  0.5x  1
20. y  2 x4  3
Ejercicio 7 (11 – 14): Determina el intervalo donde crecen o decrecen las siguientes
funciones:
11. f ( x)  x 4  8 x 3  2 x
12. f ( x)  0.5 x  4
1
13. f ( x)  3  x
2
14. f ( x)  x  3 x  70
Ejercicio 14 (9 – 12): Resuelve los siguientes problemas:
19. Un granjero desea cercar un terreno rectangular y dispone de 480m de alambrado.
Determina el área A del terreno en función del ancho x
10. Un cartel de base x y altura h tiene un área de 540cm2 con márgenes de 2cm a los
lados y 1.5cm en las partes superior e inferior. Expresa el área impresa A en función
de la base del cartel.
11. Un trazo de alambre de 100cm se parte en dos trozos, uno de ellos se doble para
formar un triángulo equilátero de x cm de lado, y el trozo restante se dobla para
formar un cuadrado. Determina el área A del cuadrado en función de x
12. La empresa García Núñez y asociados, renta departamentos de un conjunto
habitacional. La renta mensual es de $ 1 800 y tiene habitados un total de 50
departamentos. Un asesor de la empresa hace un estudio y descubre que por cada
$ 100 de rebaja en el monto de la renta, se rentarán en promedio 5 departamentos
más. Determina el ingreso I en función del número x de descuentos de $100
Ejercicio 14 EXTRA (1 – 8): Resuelve los siguientes problemas:
1. De un grupo de 28 personas se reunieron los siguientes datos, que representan
sus estaturas h , y las distancias que abarcan sus brazos abiertos horizontalmente
d (redondeadas al centímetro más cercano)
(152, 155), (165, 166), (173, 169), (183, 184), (154, 157), (161, 160), (177, 180),
(190, 189), (181, 183), (157, 153), (164, 165), (168, 172), (156, 158), (183, 185),
(178, 178), (174, 173), (175, 179), (151, 155), (159, 160), (162, 163), (179, 180),
(173, 171), (174, 178), (179, 183), (164, 166), (163, 160), (180, 178), (169, 170).
Encuentra un modelo lineal para representar estos datos
2. Se deja caer un balón de básquetbol desde una altura de aproximadamente
1.58m. La altura a la que se encuentra el balón se registra 23 veces a intervalos
de 0.02 segundos. Los resultados se muestran en la siguiente tabla:
TIEMPO (s)
ALTURA (m)
0.00
1.58
0.02
1.57
0.04
1.56
0.06
1.54
0.08
1.52
0.10
1.49
0.12
1.46
0.14
1.43
TIEMPO (s)
ALTURA (m)
0.16
1.40
0.18
1.36
0.20
1.32
0.22
1.27
0.24
1.22
0.26
1.16
0.28
1.10
0.30
1.04
TIEMPO (s)
ALTURA (m)
0.32
0.98
0.34
0.91
0.36
0.84
0.38
0.76
0.40
0.68
0.42
0.59
0.44
0.49
Encuentra un modelo cuadrático que se ajuste a estos datos. Luego utiliza
el modelo para predecir el instante en que el balón chocará contra el suelo.
3. Las parejas ordenadas dan el índice de exposición x de una sustancia
carcinógena y la mortalidad por cáncer, y , por cada 100mil personas
(3.50,150.1) , (3.58,133.1) , (4.42,132.9) , (2.26,116.7) , (2.63,140.7) , (4.85,165.5) ,
(12.65, 210.7) , (7.42,181.0) , (9.35, 312.4)
a) Determina una ecuación lineal que modele el comportamiento de los datos
anteriores
b) Utiliza la ecuación resultante para determinar la mortalidad aproximada por
cáncer por cada 100 000 personas debido a una exposición cuyo índice de
exposición x es igual a 3
4. Los datos de la tabla muestran la dureza Brinell, H , del acero, cuando se templa y
se reviene a la temperatura t (grados Farenheit) (Fuente: Standard Handbook for
Mechanical Engineers)
t
H
200
534
400
495
600
415
800
352
1000
269
1200
217
a) Utiliza las capacidades de regresión de tu calculadora para determinar un
modelo lineal para los datos
b) Usa un medio para situar los datos en un sistema de coordenadas y
construye la gráfica. ¿cuán bien se ajusta el modelo a los datos?
c) Usa el modelo para estimar la dureza del acero cuando se templa y se
reviene a una temperatura de 5000F
5. Se probó una pieza de máquina doblándola x centímetros diez veces por minuto
hasta alcanzar el tiempo t (en horas) de la falla. En la tabla se muestran los
resultados.
x
t
3
61
6
56
9
53
12
55
15
48
18
35
21
36
24
33
27
44
30
23
a) Utiliza las capacidades de regresión de un medio para construir un modelo
lineal para los datos anteriores
b) Traza la gráfica del modelo encontrado en el inciso anterior
c) Utiliza la gráfica para determinar si puede haberse cometido un error en la
medición de una de las pruebas o en el registro de los resultados. Si es así,
determina el punto erróneo y construye un nuevo modelo ajustado.
6. Los datos de la tabla muestran los costos variables para operar un automóvil en
los Estados Unidos de 1990 a 1997.Las funciones y1 , y 2 y y 3 representan los
gastos (en centavos de dólar) por milla para gasolina y aceite, mantenimiento y
neumáticos. (Fuente: American Automovile Manufactures Association)
Año
1990
1991
1992
1993
1994
1995
1996
1997
y1
5.40
6.70
6.00
6.00
5.60
6.00
5.90
6.60
y2
2.10
2.20
2.20
2.40
2.50
2.60
2.80
2.80
y3
0.90
0.90
0.90
0.90
1.10
1.40
1.40
1.40
a) Sea t el tiempo en años, donde t  0 corresponde a 1990. Utiliza las
capacidades de regresión de tu calculadora para hallar un modelo cúbico
para y1 y modelos lineales para y 2 y y 3
b) Utiliza algún medio tecnológico para construir la gráfica de y1  y 2  y3 .
Usa la gráfica para estimar el costo total variable por milla para el 2011
7. En un laboratorio, los estudiantes midieron la resistencia a la ruptura, S (en libras),
de madera de 2 pulgadas de espesor, x pulgadas de ancho y 12 pulgadas de
largo. En la tabla se muestran los resultados obtenidos:
x
S
4
2370
6
5460
8
10310
10
16250
12
23860
a) Usa las capacidades de regresión de tu calculadora para construir un
modelo cuadrático para estos datos
b) Emplea algún medio tecnológico para trazar la gráfica en un sistema
coordenado
c) Utiliza la gráfica para obtener una aproximación de la resistencia a la
ruptura cuando x  2
8. En la tabla se muestra el tiempo t (en segundos) requerido para que un Dodge
Avenger alcance una velocidad de v km / h, partiendo desde el reposo (Fuente:
Road & Track)
v
t
45
3.3
60
4.9
75
6.8
90
9.0
105
11.6
120
15.3
135
19.4
a) Usa las capacidades de regresión de un medio para construir un modelo
cuadrático para los datos
b) Utiliza un medio tecnológico para trazar la gráfica de la función encontrada
en el inciso anterior
c) Utiliza la gráfica para expresar por qué el modelo no resulta apropiado para
la determinación del tiempo requerido para alcanzar velocidades menores
a 30 km / h
d) En virtud de que la prueba se inició con arranque desde el reposo, agrega
el punto (0, 0) a los datos. Ajusta el modelo cuadrático a los datos
revisados y construye una gráfica con el nuevo modelo. ¿modela con más
exactitud el tiempo que el automóvil necesita para alcanzar bajas
velocidades? Explica
9. En la tabla se muestra la temperatura (0F) a la cual el agua hierve a presiones
seleccionadas p (en libras / in2) (Fuente: Standard Handbook for Mechanical
Engineers)
p
T
5
10
20
30
40
60
80
100
162.24 193.21 227.96 250.33 267.25 292.71 312.03 327.81
a) Usa las capacidades de regresión de un medio para construir un modelo
cúbico para los datos
b) Elabora la gráfica del modelo
c) Utiliza esta gráfica para encontrar la presión requerida para que el punto de
ebullición del agua sobrepase los 3000F
10. Busca datos de la vida real en un periódico o una revista. Ajusta los datos a un
modelo. Describe la posibles restricciones del modelo creado
Capítulo II: Límites
Ejercicio 19 (5, 6, 9, 10, 12):
Obtén los siguientes límites:
5)
lim  2 


x    x ´2 
lim  5 x  9 x 3  11x 5 


6)
x    x 2  7 x 4

lim  12 x 1  8 x 2  4 x 3 


10)
x    2 x 5  9 x 3  6 x 1 
lim  2 
12)


x    x  2  18 
lim  3x 2 


9)
x    6 x 2  5 
Capítulo III. Razón de cambio
Ejercicio 25 (1 – 9):
1. Para cada una de las siguientes gráficas, determina la razón de cambio promedio
en el intervalo especificado:
3
4
3a
b) 
4b
c)  1
a) 
d)  1
e)  
f)
0
15
8
2. Para cada una de las siguientes funciones, halla la razón de cambio promedio en
el intervalo dado:
4
a) f ( x)  x 2  2 x  1 ,
x  0, 2
b)
f ( x)  x  1 ,
c)
f ( x)  10 
1
x  3, 8
,
x
x  2, 20
x  0,100
f)
x
,
x 1
1
f ( x) 
1,
1 x2
f ( x)  x 400  x ,
g)
f ( x)  2 x ,
x  0, 5
h)
f ( x)  ( x  1)( x  3)
x   3, 2
d)
e)
f ( x) 
1
 0 .2
5
1
1

2
20

18
100

231
100

10001

x  0.1, 1.1
x  300, 400
 30
31
 6.2
5
1

3. El desplazamiento de un objeto a los t segundos de iniciado su movimiento está
dado por la ecuación s(t )  t 3  3t 2  2t t  0 donde s se mide en metros. Halla la
razón de cambio promedio (velocidad promedio) del desplazamiento durante
 30m / seg
a) los primeros 4 segundos
 38m / seg
b) el intervalo desde t  1 hasta t  4
c) el intervalo desde t  1 hasta t  2
 18m / seg
d) el intervalo desde t  1 hasta t  1  h


 h 2  6h  11 m / seg
4. El volumen del agua en un tazón semiesférico de radio r está dado por:
1
V   h 2 (3r  h) ,
3
donde h es el nivel del agua dentro del tazón. Para el caso donde r es 20 cm,
determina la tasa de crecimiento promedio del volumen de agua, desde el instante
en que el nivel del agua es de 2 cm, hasta que alcanza los 5 cm  (127 )cm 3 / cm
5. La distancia s metros que una partícula se ha movido en t segundos está dada
por la función s  4t  2t 2 , t  0 . Determina la velocidad promedio de la partícula
 (2h  16)m / seg
en el intervalo desde t  3 hasta t  3  h
6. La concentración C de un medicamento, en miligramos por mililitro, en el torrente
sanguíneo de un paciente, t horas después de una inyección está modelada
aproximadamente por la función
C (t ) 
2t
, t0
8  t3
a) Determina la concentración de medicamento en t  2
 0.25mg / ml
b) Determina el crecimiento o el decrecimiento promedio de concentración del
medicamento en el torrente sanguíneo del paciente durante el intervalo

desde t  2 hasta t  3
11
(mg / ml ) / hr
140
7. La temperatura T (en o C ) de un alimento colocado dentro de un refrigerador está
modelado por la función
T (t ) 
720
, donde t se mide en horas
t  2t  25
2
a) Determina la temperatura del alimento al instante en que fue colocado

dentro del refrigerador
144
 28.8 0 C
5
b) Determina el cambio de temperatura promedio de este alimento durante las

primeras 4 horas
864
 3.53 0 C / hr
245
8. Una cantidad de dinero es puesta en el banco y acumula intereses diariamente. La
siguiente tabla muestra el dinero acumulado en la cuenta en un periodo de 600
días.
100
200
300
400
500
600
700
t (días)
dólares
1600
1709
1823
1942
2065
2194
2328
Determina la tasa de crecimiento promedio en la cuenta durante el periodo que
abarca desde los 100 hasta los 300 días

223
 1.115 dólares / dia
200
9. La temperatura de cierta cantidad de café desde el momento en que fue vertido
dentro de una tasa fue registrado en la siguiente tabla:
0
2
4
6
9
t (min)
0
60
50
30
12
5
T ( C)
a) Sitúa estos puntos en los ejes coordenados y traza la gráfica que
representa la relación entre el tiempo transcurrido y la temperatura del café
b) Determina la tasa de decaimiento de la temperatura del café en los
intervalos de
 5 0 C / min
i.
0 a 2 minutos
 10 0 C / min
ii.
2 a 4 minutos
 9 0 C / min
iii.
4 a 6 minutos
c) ¿en cuál de los periodos anteriores la temperatura descendió más
rápidamente?
= En el intervalo de 2 a 4 minutos
Ejercicio 26 (1 – 6):
1. Para cada una de las siguientes gráficas, determina la pendiente de la recta
secante que une los puntos P y Q
a)  2  h
b)  4  h
1
1 h
2
d)  3  3h  h
c)  
2. Para cada una de las gráficas del ejercicio anterior utiliza el concepto de límite
para deducir la razón de cambio instantánea de la función dada en el punto P
a)  2
c)  1
b)  4
d)  3
3. Para cada una de las siguientes funciones, halla la pendiente de la recta secante
que une los puntos Px, f ( x) y Qx  h, f ( x  h)
b)
f ( x)  3  x 2
f ( x)  1  x 2
c)
f ( x)  ( x  1) 2  2
d)
f ( x)  x 3  x
e)
f ( x)  2  x 3
a)
 2x  h
 2x  h
 h  2x  2
 3x 2  3xh  h 2  1
 3x 2  3xh  h 2
 3x  3xh  h  2 x  h
f) f ( x)  x 3  x 2
4. Para cada uno de los incisos del ejercicio anterior determina la pendiente de la
recta tangente a las funciones dadas en el punto Px, f ( x)
a)  2x
b)  2 x
c)  2x  2
2
d)  3 x  1
2
e)  3x
f)
2
 3x 2  2 x
2
5. Para cada una de las siguientes funciones, halla la pendiente de la recta secante
que une los puntos Px, f ( x) y Qx  h, f ( x  h) y utiliza el concepto de límite
para encontrar la pendiente de la recta tangente a cada una de las funciones en el
punto P
1
1
a) f ( x)  x
b)
f ( x)  x 2
c)
f ( x)  x 3
 2x  h
 3 x 2  3 xh  h 2
 2x
 3x 2
 4 x  6 x h  4 xh  h
 4x
d) f ( x)  x 4
A partir de los resultados anteriores deduce una fórmula para la pendiente de la
recta tangente en el punto Px, f ( x) para la función f ( x)  x n , n  N
3
2
2
3
3
6. Un objeto se mueve a lo largo de un línea recta. Su posición, x metros (desde un
origen dado O ), a los t segundos está dado por x(t )  2t 2  3t  1, t  0
a) Traza la gráfica de la función
b) Muestra que la velocidad promedio en cualquier intervalo está dado por la
expresión 4t  2h  3
c) Con el resultado anterior deduce la expresión que determina la velocidad
del objeto en cualquier instante
 4t  3
Capítulo IV: La derivada
Capítulo V: Aplicaciones de la derivada