problema 8 unidad 5
Anuncio

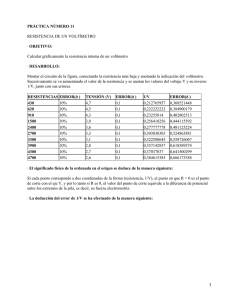
1 Problema 8 unidad 5 explicado 8) Supóngase que en los siguientes circuitos la f.e.m. de la batería es “exactamente” 12 Volt y el valor de la resistencia R es “exactamente” 100 . (a) Determinar la indicación de los instrumentos suponiendo que son ideales (La resistencia interna del amperímetro es cero y la del voltímetro es infinita) (b) Determinar la indicación de los instrumentos si la rA = 5 y rV= 5000 en cada una de las dos conexiones. (c) Determinar el valor “medido”de R para cada circuito. (d) Repetir los cálculos que se piden en (b) y en (c) para una resistencia de 158 (e) Repetir los cálculos para R = 300 (f) Demostrar que el valor “medido” de R utilizando la conexión “corta” es igual al paralelo de rV con R (g) Demostrar que el valor “medido” de R utilizando la conexión “larga” es igual a R + rA Conexión “corta” Conexión “larga" (a) La d.d.p. en R es igual a la d.d.p entre los bornes de la batería (f..e.m) ya que si la rA = 0 para cualquier valor de la corriente la caída de potencial en el amperímetro es nula. Como rV , el paralelo de R con rV es igual a R.. Por lo tanto I = 12 V/ 100 = 0,12 A = 120 mA. El amperímetro indicará 120 mA y el voltímetro 12 V. (b) “CORTA”: La resistencia del circuito se obtiene haciendo el paralelo entre R y r V y dicha resistencia en serie con rA : 1 1 1 r R 5000 100 Req rA rA V 5 5 98,039 103,039 r R r R 5100 v V La corriente que entrega la batería y que por lo tanto es la que pasa por el amperímetro es: 12V (indicación del amperímetro) I 0,116 A 103,039 La caída de potencial en el amperímetro es: V A 0,116A 5 0,582V y por lo tanto la caída de potencial en la resistencia R es: VR 12V 0,582 V 11,418V (indicación del voltímetro) A este método también se lo denomina de la “tensión bien medida” ya que el voltímetro mide la d.d.p de potencial en la R, mientras que el amperímetro mide una intensidad de corriente que es mayor a la corriente que pasa por R. La corriente I se divide. Parte de ella (0,114 A) pasa por R y una pequeña parte(0,002 A) pasa por el voltímetro. (b) “LARGA”: La resistencia equivalente se obtiene haciendo el paralelo de la rV con la serie de rA y R: 2 1 1 Req rv R rA 1 rV R rA 5000 100 5 102,840 rV rA R 5105 La corriente que entrega la batería es I 12V 0,117 A 102,840 Pero la corriente que pasa por el amperímetro, y por R, es: I R 12V 0,114 A (indicación 105 del amperímetro) Este método también es denominado de la “corriente bien medida” ya que efectivamente el amperímetro mide la misma corriente que pasa por la resistencia R Por supuesto el voltímetro mide 12 Volt ya que se encuentra conectado entre los bornes de la batería Tanto en la conexión corta como en la conexión larga pasa por el voltímetro una pequeña corriente. En este caso es I V 0,117A 0,114 A 0,003A 3 mA . Es indispensable que circule corriente por el interior del voltímetro, ya que dicha corriente es necesaria para el instrumento funcione. (c) Valores “medidos” de R. Si sólo disponemos de la lectura del amperímetro y del voltímetro la única V manera de determinar el valor de R es aplicando la ley de Ohm: R V IA Es decir, si suponemos que conectamos un amperímetro y un voltímetro con una resistencia R desconocida y con una fuente de tensión de f.e.m también desconocida y queremos saber el valor de R, debemos confiar en los valores que indican los instrumentos. CORTA LARGA VV 11,418 V 12,000 V IA 0,116 A 0,114 A R “medida” 98,431 105,263 Como en este ejercicio sabemos el valor de R, y lo consideramos exacto en 100 , los cálculos precedentes nos indican que “medir” una resistencia con un voltímetro y una amperímetro implica que la medición (indirecta) de R tiene un error. En este ejemplo, en la conexión corta ese error en R es 1,569 por defecto. En la conexión larga el error es 5,263 por exceso. Pero en la realidad nunca podemos saber el valor “verdadero” de R ya que todo método para medirla tendrá error. Entonces si procedemos como indica el ejercicio sólo podríamos decir que nuestra medición de R nos indica que su valor está entre 98,431 y 105,263 . Entonces una posibilidad es adoptar como valor “más probable” o “representativo” de la medición al promedio entre estos valores extremos. Y como error absoluto a la semiamplitud de dicho intervalo. Entonces…. R mín R máx 98,431 105,263 101,847 2 2 R Rmín 105,263 98,431 R máx 3,416 2 2 R (101,8 3,4) (redondeado) 3,4 R 0,033 3,3 % 101,8 Ro 3 (f) Todos los cálculos anteriormente realizados nos muestran que el valor de R obtenido a partir de la medición de la diferencia de potencial y de la intensidad de corriente, tiene un error provocado por la influencia de los instrumentos en el proceso de medición. Esta influencia en eset caso está determinada por los valores de la resistencia interna de los instrumentos. Si la resistencia interna del amperímetro fuera nula y la resistencia interna del voltímetro fuera infinita, entonces la medición sería exacta. Pero si la resistencia del voltímetro fuera infinita la corriente que circularía por él sería nula y el instrumento no funcionaría. En consecuencia en una medición real el valor medido de R tiene un error “inevitable” provocado por el método de medición. Ahora bien, si sabemos que la medición tiene error y sabemos cuáles son sus causas, ¿no podremos “evitar” ese error? Quizás podamos realizar una corrección al medición realizada para reducir ese error. Conexión “CORTA”. El valor medido de R se obtiene dividiendo la d.d.p que mide el voltímetro (“bien medida”) por la corriente que mide el amperímetro (suma de las corrientes por la resistencia y por el voltímetro) RM R VV VV r R rV // R V VV IA rV R rV // R rV // R R R R rV R rV R r 1 V R rV R Como podemos apreciar el valor medido RM se aproxima a R cuanto mayor sea rV con respecto a R. Además el error relativo estará cerca de cero si rV >>>R.. Conexión “LARGA”. VV I A rA R RM rA R IA IA R rA R R R rA R Si rA pudiera ser cero, entonces el valor medido RM coincidiría con el valor “verdadero” R. El error relativo sería cero. Si las resistencias internas de los instrumentos son conocidas podemos estimar el error relativo para cada método en función del valor de R que se quiere medir. Es decir si se conoce el orden de magnitud de la R que quiere ser medida podemos ver que el error relativo es función de R. ¡De la R que no conocemos porque es lo que se quiere medir! Si graficamos ambas funciones “error relativo = f (R)” podemos determinar cuál de las dos conexiones nos resulta más conveniente en función del orden de magnitud de la R a medir. Con los datos de nuestro problema rV = 5000 y rA = 5 , el gráfico resulta el siguiente. 4 La línea de trazos representa a la función correspondiente a la conexión corta. Es aproximadamente una recta cuya pendiente es 1/rV. Como podemos apreciar no es conveniente utilizar este método para valores “grandes” de R ya que el error relativo crece aproximadamente en forma lineal con el valor de R. Si los valores de R que se quieren medir son menores a 400 , el error relativo resulta menor al 10% (ene este caso en que rV= 5000 ) La línea continua representa a la función para el caso de la conexión larga. En este caso da una función que decrece con R. Es decir es el método recomendado para valores “grandes” de R. Cuánto más grande sea el valor de R que se quiere medir, más pequeño resulta el error. Como vemos en el gráfico si medimos valores de R mayores a 200 , obtenemos errores relativos menores a 5 %. En el gráfico se puede ver que existe un valor de R para el cual ambos métodos dan el mismo error relativo. Dicho valor está entre 100 y 200 y en ese caso el error relativo es algo menor al 5 %.