Sistemas Lineales Invariantes en el Tiempo (SLTI)
Anuncio

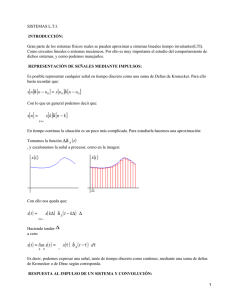
Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 1 de 10 Sistemas Lineales Invariantes en el Tiempo Para comenzar a estudiar los sistemas, debemos primero considerar el concepto de señal. Si bien es un término de muy amplio alcance, en el contexto que nos atañe consideramos como señal a toda variación de una cantidad física (por lo general con el tiempo) susceptible de ser representada matemáticamente y de la cual podemos obtener alguna información o realizar algún cambio. Según su naturaleza podemos clasificar a las señales en dos grupos, a saber: las que pueden definirse en cada instante de un determinado intervalo, llamadas señales de tiempo continuo, y aquéllas que pueden representarse como una sucesión de de valores ordenados mediante un índice entero, llamadas señales de tiempo discreto. (El uso de la palabra "Tiempo" establecida por el uso alude a que la mayoría de las señales procesadas dependen del tiempo, sin ser éste el caso general). Con esto, definiremos como sistema a cualquier ente físico o proceso capaz de recibir una señal, denominada de entrada, o excitación ( x(t) ), y transformarla en otra señal que denominaremos de salida o respuesta. ( y(t) ) Según la naturaleza de las señales que los sistemas procesan, usualmente se los clasifica tambien como "de tiempo continuo" o "de tiempo discreto". Como puede apreciarse, las definiciones previas son de carácter muy general. Esto pone en evidencia una de las grandes ventajas de la teoría de señales y sistemas, esto es: puede aplicarse al estudio de una gran cantidad de problemas reales de muy diversa naturaleza física. En este trabajo centraremos nuestra atención en un tipo particular de sistemas, denominados “Sistemas Lineales e Invariantes en el Tiempo” o “SLTI”, Nota: Si bien este trabajo está desarrollado en tiempo continuo, pueden hallarse relaciones totalmente análogas para los sistemas de tiempo discreto Linealidad Se dice que un sistema es lineal si cumple con el llamado principio de superposición, el cual a su vez se compone de dos partes : 1. Homogeneidad: si x(t ) y(t ) kx(t ) ky(t ) (1) 2. Aditividad: si x1(t ) y1(t ) x 2(t ) y2(t ) x1(t ) x 2(t ) y1(t ) y2(t ) (2) Combinando la (1) y la (2): k1 x1 (t ) k 2 x2 (t ) k1 y1 (t ) k 2 y2 (t ) (superposición) Evidentemente, esto se cumplirá si el sistema, para obtener la salida, efectúa sobre la señal de entrada operaciones que son matemáticamente lineales, como ser: suma, multiplicación por una constante, diferenciación e integración. A partir de esto es importante entender porqué las ecuaciones íntegro-diferenciales lineales son la herramienta apropiada para modelar matemáticamente la relación entrada-salida de este tipo de sistemas, ya que en ellas, en su forma general, intervienen todas las operaciones antedichas. Invariabilidad Temporal Decimos que un sistema es invariante en el tiempo, si la respuesta del mismo no depende del momento en que es excitado, formalmente: Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 2 de 10 si x (t ) y(t ) x (t t 0 ) y(t t 0 ) (3) Esta es una propiedad importante del sistema, puesto que lo hace más predecible y posibilita su análisis por medio de los métodos que estudiaremos mas adelante. Físicamente, la invariabilidad temporal implica que los constituyentes de nuestro sistema, no se alterarán y conservarán sus propiedades con el paso del tiempo: "sus parámetros son constantes" Por ejemplo, un circuito electrónico no sería invariante en el tiempo si sus componentes (resistencias, inductores, condensadores, etc...) cambiasen de valor, como sucede por degradación de los materiales que los componen, lo cual en general es un proceso lento. Es importante señalar que la invariabilidad temporal del sistema establece que la ecuación diferencial lineal que lo define sea a coeficientes constantes, pues dichos coeficientes están definidos por los componentes físicos del sistema (resistencias, inductores, masas, resortes, amortiguadores, etc.). Consecuencias Importantes El hecho de que un sistema sea LTI, hará más manejable su análisis: puesto que es posible descomponer a una señal arbitraria en componentes más simples, hallar las respuestas del sistema a cada una de ellas, y luego, por el principio de superposición, sumar dichas respuestas para obtener la respuesta total a la entrada arbitraria (compuesta). Esta forma de tratamiento, como se verá, sirve de base para varios métodos de análisis de SLTI, en particular: 1 2 3 La interpretación de una señal arbitraria como una suma de impulsos ponderados, es la base del método de convolución, que caracteriza al sistema en función de su respuesta impulsiva. La representación de la señal de entrada como una suma de sinusoides armónicas ponderadas, conduce a las Series de Fourier. La descomposición de una señal arbitraria en una suma de exponenciales complejas ponderadas, es una serie de Fourier de tipo exponencial y es la base para el estudio por medio de las transformadas de Fourier y de Laplace. Método de Convolución Ahora profundizaremos sobre el primero de los métodos de análisis de SLTI antes mencionados. El método de convolución sirve para hallar la respuesta del sistema a una entrada arbitraria, conociendo previamente la respuesta impulsiva del mismo. Llamamos repuesta impulsiva, h(t), a la respuesta del sistema cuando es excitado con la señal delta de Dirac o simplemente, impulso δ (t) ( nos referiremos al impulso unitario, o sea de área = 1 ). Ésta es una señal que posee amplitud infinita, duración infinitesimal y área finita. Como puede deducirse de sus características, δ (t) es una señal meramente teórica y no reproducible en la práctica. Por lo tanto, debemos conformarnos con aproximarla mediante un pulso de una amplitud y duración determinados de manera tal que el error cometido esté dentro los márgenes aceptables para el caso. Una de las propiedades más importantes del impulso es, como sabemos, la de muestreo de una señal, o selección del impulso. Esto es: x(t ) ( t ) x( ).d Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 3 de 10 Propiedad que puede verificarse fácilmente. Este tipo de integrales no se evalúa analíticamente por los métodos clásicos. Hay que ver que el producto en el integrando es, en definitiva, la δ (-t) con área (coeficiente) = x(t) ubicada en = t. Podemos sacar x(t) que actúa como coeficiente, de la integral que procede ( se evalua) por . Así: x(t) = x(t) δ (-t) d = x(t) dado que el área de δ (-t) =1 - Aquí podemos ver cómo una señal cualquiera puede ser representada como una “suma“ (considerando a la integral como el límite de una suma) de impulsos desplazados en el tiempo y ponderados por el valor de la señal en ese instante. Esto puede verse de una manera más gráfica en tiempo discreto, o bien, si lo consideramos como el límite de la aproximación de la señal por medio de pulsos rectangulares tomando en el intervalo una mayor cantidad de pulsos de menor duración. Aquí esta la clave del método de convolución, a saber: a. Ya que podemos representar cualquier señal como una “suma” de impulsos ponderados; si excitamos un SLTI con una señal arbitraria x(t) es posible, gracias al principio de aditividad, determinar la salida analizando únicamente las respuestas a cada uno de los impulsos que la componen y luego sumarlas. b. Si bien es cierto que el proceso de encontrar las respuestas a todos los impulsos que componen x(t) podría parecer en principio un trabajo tedioso y quizás imposible (pues en tiempo continuo la señal está compuesta por infinitos impulsos) , puede solucionarse esto considerando que los impulsos que componen la señal difieren unos de otros únicamente en su posición temporal y su “ponderación” (determinada por la constante que los multiplica); así, podremos representarlos genéricamente como K δ (t-to) y ver que, haciendo uso de otras dos propiedades de los SLTI, la homogeneidad e invariancia en el tiempo, la respuesta a este impulso genérico será K h(t-to), donde h(t) es la respuesta al impulso unitario ubicado en el origen y constituye la incógnita real del problema, ya que K y to dependen de la señal de entrada. En síntesis, si conocemos h(t) podremos obtener las respuestas de todos los impulsos que conforman x(t) y luego sumando dichas respuestas obtener la respuesta “completa” del sistema a x(t), o sea y(t). Todo este proceso expresado matemáticamente nos permite llegar a la expresión general para obtener la respuesta y(t) de un SLTI, caracterizado por su respuesta impulsiva h(t), a una entrada x(t) dada. Esta expresión es conocida como integral de convolución: y (t ) x ( )h(t )d x (t ) h(t ) (4) Nota: Para la contraparte discreta, denominamos a este proceso suma de convolución. Con esta expresión, trabajaremos en el desarrollo de los ejemplos que siguen: A) Ejemplo 1. Dado el siguiente circuito: R + + Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 4 de 10 Con: R= 1 [MΩ] y C= 1 [μf] x(t) i(t) C y(t) - - a. Hallar la ecuación diferencial que establece la relación entrada salida. Las relaciones volt-ampere (ley de Ohm) de los componentes del circuito son: Resistor: vR (t) R i R (t) (5) Capacitor: iC (t ) C ; dvC (t ) (6) dt Utilizando la ley de las tensiones de Kirchhoff, podemos escribir: Utilizando (5): x (t) vR (t ) y(t ) x (t) R i(t ) y(t ) R ic (t ) y(t ) Utilizando (6): x (t ) R C dvC (t ) y (t ) (7) dt Reemplazando valores: x (t ) R C dy (t ) dy (t ) y (t ) y (t ) (8) dt dt Que es la relación entrada-salida que define el sistema en cuestión. b. Verificar si el sistema determinado por el circuito es lineal e invariante en el tiempo. Para que el sistema sea lineal debemos verificar: I) Homogeneidad: Si multiplicamos ambos miembros de (8) por una constante arbitraria K obtenemos dy (t ) Kx(t ) K R C y (t ) dt Luego distribuyendo la K en el segundo miembro Kx(t ) R C d Ky (t ) Ky (t ) dt Aquí puede apreciarse como a la entrada Kx(t) le corresponde la salida Ky(t), ósea se cumple la (1) y el sistema es homogéneo. II) Aditividad: Según (8) es posible escribir para dos entradas x1 (t) y x2 (t) cualesquiera: dy1 (t ) y1 (t ) dt dy (t ) x 2(t) R C 2 y2 (t ) dt x 1(t) R C Sumando estas dos expresiones miembro a miembro, obtenemos. x 1(t) x 2(t) R C dy1 (t ) dy (t ) y1 (t ) R C 2 y2 (t ) dt dt x1(t ) x 2 (t ) R C d y 1(t ) y 2 (t ) y1(t ) y 2 (t ) dt Reordenando. Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 5 de 10 Aquí puede apreciarse como a la entrada x1 (t) + x2 (t) le corresponde la salida y1 (t) + y2 (t), o sea, se cumple la (2) y el sistema es aditivo. Con esto se concluye en que el sistema es Lineal. Esto podría haberse deducido con el solo hecho de analizar la ED que define el sistema, la (7), ya que como dijimos, si un sistema sólo realiza operaciones matemáticamente lineales para obtener la salida, evidentemente nuestro sistema será “lineal”. Esto se refleja al ver cómo las verificaciones de la homogeneidad y aditividad del sistema se lograron gracias a que las operaciones matemáticas que intervienen (diferenciación, suma y multiplicación por una constante) poseen estas mismas propiedades. Respecto a la invariabilidad en el tiempo del sistema, podemos ver como ésta se cumple considerando que los coeficientes de la (8), a saber, los valores de R y C, se mantienen constantes en el tiempo (idealmente). Así si excitamos el circuito en diferentes momentos con una misma señal obtendremos la misma respuesta en los respectivos distintos momentos (aquí tomamos al circuito descargado, o sea que en el capacitor no hay energía almacenada al momento de excitarlo), pues si los componentes (y su interconexión) no varían sus características, el sistema que conforman es el mismo. (Recordemos también que la determinación de h (t) supone el sistema sin energía inicial = en reposo) Es importante recordar que todo sistema está definido totalmente por la ED que establece la relación entre su entrada y su salida, y a su vez toda ED lineal de un orden determinado se define totalmente por los coeficientes que en ella intervienen. c. Hallar la respuesta impulsiva Considerando x(t) = δ (t), la (8) queda. (t) R C dy (t ) y (t ) (9) dt (Tengamos presente que al perturbar con el impulso, la salida y(t) coincide con h(t)). Dividiremos el análisis en tres partes: 1. Para: t<0, δ (t)=0 El sistema no ha sido perturbado y puesto que lo consideramos relajado (condiciones iniciales nulas) y es pasivo (sin fuentes de energía internas), la salida será nula. Y(t)=0 para todo t<0 2. Para t>0, δ (t)=0 La (9) queda: RC dy (t ) y (t ) 0 dt Que, como sabemos, posee una solución del tipo: y(t ) Ke t RC Para t>0 Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 6 de 10 Donde K es una constante arbitraria que quedará definida por lo que suceda en el instante cero. 3. Sólo nos resta saber qué sucede cuando t=0. Este caso podemos analizarlo integrando ambos miembros de (9) entre los instantes 0- y 0+. 0 0 0 dy(t ) dt y(t )dt dt 0 0 (t)dt R C 0- 1 RC y (0) y (0) 0 y(t )dt 0 0 El termino y (t )dt será nulo salvo que y(t) posea una singularidad de orden superior en el origen. 0 dy (t ) sería un doblete unitario o singularidad de orden superior, y puesto dt Sin embargo, si así fuese, 0 que en el primer miembro de (9) no hay ningún doblete se deduce que y (t )dt 0 0 1 RC y(0) y(0) 1 Pero y(0-)=0, así y (0) y la respuesta impulsiva del sistema queda : RC t 1 RC h(t ) e u (t ) RC Con esto: Reemplazando valores, RC = 1: H L h(t ) et u(t ) h t 0.7 0.6 0.5 0.4 0.3 0.2 0.1 t 1 2 3 4 5 6 7 Podríamos haber llegado al mismo resultado derivando la respuesta del sistema al escalón unitario, u(t). Pues: Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 7 de 10 u (t ) y u (t ) dy (t ) du(t ) u dt dt dy (t ) (t ) u h(t ) dt du (t ) (t ) dt ; Pero Este método es más práctico ya que la función escalón es más fácil de sintetizar con un menor error que la función impulso. d. Verificar si el sistema es: causal , BIBO y con memoria El sistema será causal si la salida y(t) no depende de entradas futuras tales como x(t+1). El sistema no puede alterar o generar a la y(t) en función de entradas futuras, es decir, no puede actuar de manera anticipativa; por ello a los sistemas causales se los denomina no anticipativos. Una definición formal de causalidad requiere que entradas idénticas de una cierta duración produzcan respuestas idénticas de la misma duración. En un sistema con memoria o dinámico la respuesta presente depende a la vez de entradas presentes y pasadas, esto se debe a los elementos almacenadores de energía que pueda contener el sistema en cuestión. En el sistema representado por nuestro circuito, el almacenador de energía es el condensador; se trata de un sistema con memoria. La estabilidad BIBO (Bounded Input, Bounded Output = entrada acotada, salida acotada) implica que cada entrada acotada, resulta en una salida acotada. Una condición necesaria y suficiente para que el SLTI sea considerado estable (BIBO), consiste en que cada raíz de su ecuación característica debe tener una parte real negativa (y la derivada más alta de la entrada no debe exceder a la de la salida). Siendo el SLTI descrito por la ecuación: y ( n ) (t ) a1y ( n 1) (t ) an y (t ) b0x ( m ) (t ) b1y ( m 1) (t ) bm y (t ), m n e. Hallar la respuesta a la entrada , x(t) = 15 Sen (10t). u(t) por el método de convolución Considerando los datos y la h(t) calculada en el punto c, la respuesta del sistema queda: y(t ) x(t ) * h(t ) 15.Sen(10 )u ( ).e ( t ) u (t )d 15e t t Sen(10 ).e d 0 Integrando por partes obtenemos: (no desarrollar esta expresión) t e et et t y (t ) 15et [ ( Sen ( 10 ) 10 . Cos ( 10 )) 15 e [ ( Sen ( 10 t ) 10 . Cos ( 10 t ))] 150 ] 0 1 102 1 102 1 102 y(t ) 0,148Sen(10t ) 1,48Cos(10t ) 1,48et Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 8 de 10 ht 2 1 t 1 2 3 4 5 -1 B) Ejercicio: Realizar los puntos a y c del ejemplo (A) para el siguiente sistema discreto: x[n] + y[n] z-1 1/3 a) La ecuación en diferencias que define el sistema es: y[n] – 1/3 y[n-1] = x[n] (10) La cual surge por simple inspección de los constituyentes del sistema. c) Si perturbamos el sistema con un impulso unitario la (10) queda: h[n] – 1/3 h[n-1] = d[n] (11) Para n<0: Puesto que consideramos el sistema relajado y el impulso se produce en n=0, no habrá salida antes de este “tiempo”. Así: h[n] = 0 ; n<0 (12) Para n>0: Dada la ubicación temporal del impulso (n=0), para tiempos correspondientes a n>0 la (11) queda: h[n] – 1/3 h[n-1] = 0 (13) De manera análoga a las ED de tiempo continúo, se asume una solución exponencial de tipo : h[n] n Reemplazando en la (13): n n1 3 0 Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución 1 U. T. N. 2007 Página 9 de 10 1 0 3 1/ 3 Con esto: 1 h[n] 3 n ; n>0 (14) Relación que me permite, conociendo h[0] (condición inicial) obtener h[n] para toda n>0 Para n=0: Para este caso la (11) queda. Tomando n=0 y d[0]=1 h[0] – 1/3 h[-1] = 1 Sin embargo ya vimos que para n<0 la salida es nula, entonces: h[0] = 1 (15) Así, considerando (13), (14) y (15) la respuesta impulsiva queda definida como: n 1 h[n] u[n] 3 Donde u[n] es el escalón unitario discreto En base a la h[n] obtenida (su duración) se dice que el sistema es IIR (Infinite impulse response o de respuesta al impulso infinita) h n 1 0.8 0.6 0.4 ... 0.2 n 1 2 3 4 5 6 1 n , n 0,1,...,7 e) Hallar la respuesta del sistema a la entrada x[n] 2 . Por el método de 0 convolución. La expresión que da la respuesta de un sistema LTI discreto y relajado en base a su respuesta impulsiva (método de convolución) es: Análisis de Señales y Sistemas TP: Sistemas Lineales y convolución U. T. N. 2007 Página 10 de 10 y[n]= x[n] * h[n] y[n] x[k ].h[n k ] k k 1 1 y[n] u[k ]u[7 k ] 3 k 2 1 y[n] 3 n k 1 y[n] 3 n n k nk u[n k ] 3 u[7 k ]u[n k ] k 0 2 3 u[7 k ] ; n 0 k 0 2 y n 1 0.8 0.6 0.4 ... 0.2 n 1 2 3 4 5 6 7 Los primeros términos son: 1, 5 6 , 19 36 , 65 216 , 211 1296 , 665 7776 , 2059 46656 , 6305 279936 , 6305 839808