Contenidos y ejercicios psu: funcion lineal

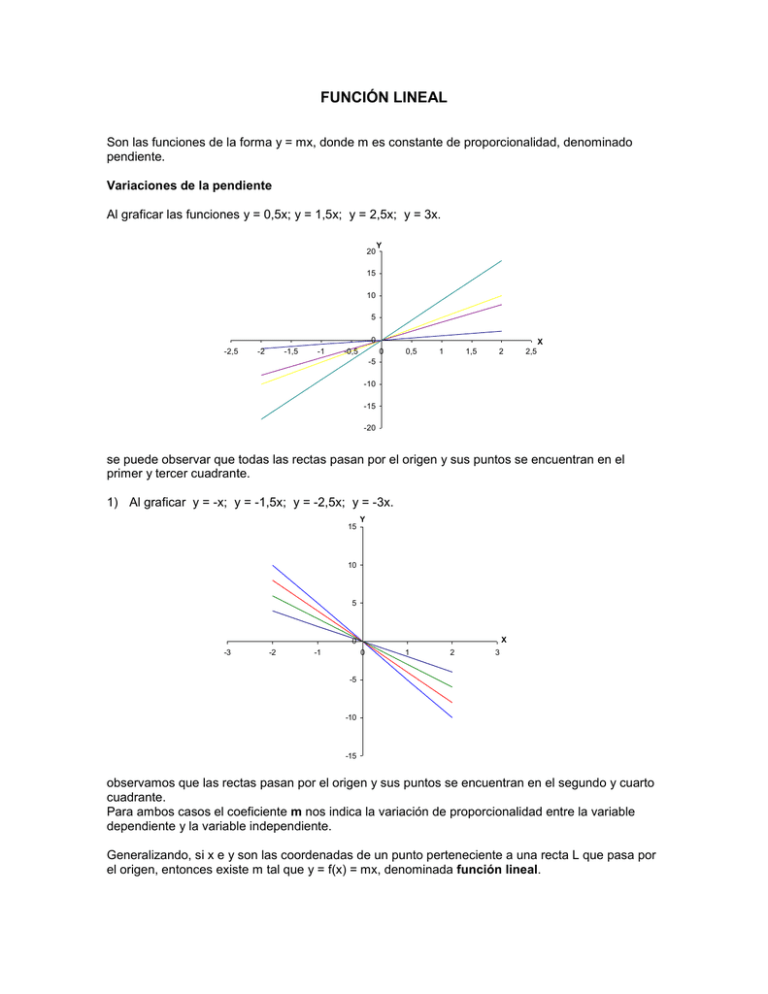
FUNCIÓN LINEAL
Son las funciones de la forma y = mx, donde m es constante de proporcionalidad, denominado
pendiente.
Variaciones de la pendiente
Al graficar las funciones y = 0,5x; y = 1,5x; y = 2,5x; y = 3x.
20
Y
15
10
5
0
-2,5
-2
-1,5
-1
-0,5
X
0
0,5
1
1,5
2
2,5
-5
-10
-15
-20
se puede observar que todas las rectas pasan por el origen y sus puntos se encuentran en el
primer y tercer cuadrante.
1) Al graficar y = -x; y = -1,5x; y = -2,5x; y = -3x.
15
Y
10
5
X
0
-3
-2
-1
0
1
2
3
-5
-10
-15
observamos que las rectas pasan por el origen y sus puntos se encuentran en el segundo y cuarto
cuadrante.
Para ambos casos el coeficiente m nos indica la variación de proporcionalidad entre la variable
dependiente y la variable independiente.
Generalizando, si x e y son las coordenadas de un punto perteneciente a una recta L que pasa por
el origen, entonces existe m tal que y = f(x) = mx, denominada función lineal.
También, viendo los gráficos concluímos que si m > 0, entonces y = mx es una función creciente y
que si m < 0, entonces y = mx es una función decreciente. Por lo tanto, el valor de m nos indica la
orientación de la recta.
Función Afín
Las variables x e y están relacionadas por una función afín si satisfacen una ecuación de tipo y =
mx + n, en la cual m y n son constantes.
Concepto de Recta
Una recta es la representación gráfica de una función de primer grado. Toda función de la forma y
= ax + b de IR en IR representa una linea recta.
Se denomina a x variable independiente ya que puede tomar cualquier valor, mientras que y se
llama variable dependiente, ya que su valor está determinado por el valor que tome x.
Si un par de valores (x,y) pertenece a la recta, se dice que ese punto satisface la ecuación.
Ejemplo: El punto (7,2) satisface la ecuación y = x - 5, ya que al reemplazar queda 2 = 7 - 5 lo que
resulta verdadero.
La ecuación de la recta puede ser representada en dos formas:
Forma General: ax + by + c = 0
Forma Principal: y = mx + n
Pendiente de una Recta
En la ecuación principal de la recta y = mx + n, el valor de m corresponde a la pendiente de la recta
y n es el coeficiente de posición.
La pendiente permite obtener el grado de inclinación que tiene una recta, mientras que el
coeficiente de posición señala el punto en que la recta interceptará al eje de las ordenadas.
Ejemplo: La ecuación y = 4x + 7 tiene pendiente 4 y coeficiente de posición 7, lo que indica que
interceptará al eje y en el punto (0,7).
Cuando se tienen dos puntos cualesquiera (x 1,y1) y (x2,y2), la pendiente queda determinada por el
cuociente entre la diferencia de las ordenadas de dos puntos de ella y la diferencia de las abscisas
de los mismos puntos, o sea
m
y 2  y1
x 2  x1
Una recta que es paralela al eje x, tiene pendiente 0.
Ecuación de la recta que pasa por dos puntos
Sean P(x1,y1) y Q(x2,y2) dos puntos de una recta, la ecuación de la recta que pasa por dos puntos
es:
y 2  y1 y  y1

x2  x1 x  x1
que también se puede expresar como
y  y1  ( x  x1 )
y 2  y1
x2  x1
Ejemplo:
Determina la ecuación de la recta que pasa por los puntos P(1,2) y Q(3,4)
y2 42

x 1 3 1
y2 2

x 1 2
y2
1
x 1
y-2=x-1
x-y+1=0
Ecuación de la recta dado punto-pendiente
La ecuación de la recta que pasa por dos puntos está determinada por
y 2  y1 y  y1

x2  x1 x  x1
pero
m
y 2  y1
x 2  x1
luego reemplazando en la ecuación anterior se obtiene
m
y  y1
x  x1
despejando, obtenemos que:
y - y1 = m(x - x1)
Ejemplo: Determina la ecuación general de la recta de pendiente -4 y que pasa por el punto (5,-3)
y - y1 = m(x - x1)
y - (-3) = -4(x - 5)
y + 4 = -4x + 20
Luego la ecuación pedida es 4x + y - 16 = 0.
Rectas Paralelas, coincidentes y perpendiculares
Dos rectas son paralelas cuando sus pendientes son iguales y sus coeficientes de posición
distintos, o sea
L1: y = m1x + n1
L2: y = m2x + n2,
Entonces L1 // L2 sí y sólo si m 1 = m2; n1 distinto a n2
Ejemplo: Las rectas y = 4x + 5 ; y = 4x - 2 son paralelas.
Dos rectas son coincidentes cuando sus pendientes son iguales y sus coeficientes de posición
iguales, o sea
L1: y = m1x + n1
L2: y = m2x + n2,
Entonces L1 coincidente con L2 sí y sólo si m1 = m2 y n1 = n2
Dos rectas son perpendiculares cuando el producto de sus pendientes es -1, o sea
L1: y = m1x + n1
L2: y = m2x + n2,
Entonces L1  L2 sí y sólo si m1· m2 = -1
Ejemplo:
L1: y = -2x + 3
L2: y = 0,5x - 4
Entonces L1  L2 ya que -2 · 0,5 = -1
EJERCICIOS
1. En la función lineal 3y = -6x + 1, el valor de la pendiente es:
a) -6
b) -2
c) 1/3
d) 1
e) 3
2. La ecuación de la recta que pasa por el punto (1,-4) y es paralela con la recta x + 5y – 3 = 0, es:
a) –x+y+5=0
b) x+5y+19=0
c) x+y+3=0
d) –5x+y+9=0
e) x+5y+21=0
3. La ecuación de la recta que pasa por el punto (5,6) y que es paralela con la recta que une los
puntos (-4,0) y (1,-6) es:
a) –5x+6y=11
b) 6x+5y=60
c) -6x+5y=0
d) –5x-6y=0
e) y-2x=-4
4. El perímetro del triángulo cuyos vértices son (3,0); (3,4) y (0,4), es:
a) 5
b) 6
c) 12
d) 16
e) 25
5. ¿Cuál de los siguientes puntos pertenece a la recta 3x + 2y – 4 = 0
a) (0,2)
b) (2,2)
c) (-2,2)
d) (0,-2)
e) (1,-1)
6. La pendiente de la recta que pasa por los puntos P(6,-2) y Q(-8,4), es:
a) -7
b) –7/3
c) -1
d) –3/7
e) –1/7
7. Determinar el valor de K de modo que el punto (4,-3) pertenezca a la recta Kx – y = -2.
a) K = -5/4
b) K = -2/3
c) K = -2/7
d) K = 1/4
e) K = 4
8. Dadas las rectas L1: y = Kx-3 y L2: y = 2x – 4K. Determinar el valor de K para que L1//L2.
a) K = 2
b) K = 4/3
c) K = 3/4
d) K = -2
e) K = -3
9. Determinar el valor de K para que las rectas y + 3 = Kx y 2x = -4K – y sean perpendiculares.
a) K = 3/4
b) K = 1/2
c) K = -1/2
d) K = –4/3
e) K = -2
10. Determina el coeficiente de posición de la función 4x – 3y – 5 = 0
a) 4
b) 4/3
c) –5
d) -3
e) –5/3
ALTERNATIVAS
1.
Alternativa A: Incorrecta. El coeficiente de x es la pendiente, siempre y cuando esté despejada y,
no siendo este el caso.
6 x  1
Alternativa B. CORRECTA. Al despejar y se obtiene que y 
, entonces m = -6/3, o sea la
3
pendiente es -2.
Alternativa C. Incorrecta. Corresponde al coeficiente de posición.
Alternativa D: Incorrecta. No esta despejado y, por lo tanto 1 no corresponde ni a la pendiente ni al
coeficiente de posición.
Alternativa E: Incorrecta. Este valor, no corresponde ni a la pendiente ni al coeficiente de posición.
2.
Alternativa A: Incorrecta. Se considera la pendiente igual a 1, pero sin despejar y, lo que es un
error.
3 x
Alternativa B. CORRECTA. Al despejar y se obtiene y 
, o sea la pendiente es –1/5.
5
1
Entonces la recta queda determinada por y  4   ( x  1) que al resolver resulta x+5y+19=0
5
Alternativa C. Incorrecta. Se da el valor –1 a la pendiente lo que conduce a una ecuación de la
recta equivocada.
Alternativa D: Incorrecta. Se considera la pendiente como 5, lo que no corresponde según la
ecuación dada.
Alternativa E: Incorrecta. Se determina la pendiente y luego al resolver se produce un error al
despejar y.
3.
Alternativa A: Incorrecta. Se determina la pendiente en forma equivocada, obteniéndose –5/6.
Alternativa B. CORRECTA. Primero se determina la pendiente que va a corresponder a ambas
6  0 6
rectas, por ser paralelas. m 
. Luego, por la fórmula punto-pendiente se obtiene que

1 4
5
6x+5y=60.
Alternativa C. Incorrecta. Se calcula la pendiente como 6/5, lleva a la ecuación –6x + 5y = 0
Alternativa D: Incorrecta. Error al determinar la pendiente como 5/6, lleva a la ecuación –5x – 6y =
0
Alternativa E: Incorrecta. Se calcula m = 2, en forma equivocada lo que lleva a la ecuación y – 2x =
-4.
4.
Alternativa A: Incorrecta. Se determina correctamente la hipotenusa, pero luego no se calcula el
perímetro solicitado.
Alternativa B. Incorrecta. Corresponde al valor del área del triángulo y no del perímetro.
Alternativa C. CORRECTA. Se calcula la hipotenusa por el teorema de Pitágoras, que da 5 y luego
se suman las medidas de los lados del triángulo para determinar el perímetro pedido.
Alternativa D: Incorrecta. Se suman los catetos al cuadrado, pero confundido con los dobles, o sea
6 + 8.
Alternativa E: Incorrecta. Se utiliza mal el teorema de Pitágoras y se obtiene 25 para la hipotenusa.
No se determina el perímetro.
5.
Alternativa A: CORRECTA. Para determinar si el punto pertenece a la recta hay que reemplazarlo
en la ecuación y verificar la igualdad. Entonces al reemplazar resulta 3(0) + 2(2) – 4 = 0
Alternativa B. Incorrecta. Se reemplaza el punto (2,2) y resulta 6 + 4 – 4 = 6, distinto de 0.
Alternativa C. Incorrecta. Al reemplazar (-2,2), se obtiene –6 + 4 – 4 = -6, distinto de 0.
Alternativa D: Incorrecta. Se reemplaza (0,-2), se obtiene 0 –4 – 4 = 0, distinto de 0.
Alternativa E: Incorrecta. Se reemplaza (1,-1), se obtiene 3 – 2 –4 = -3, distinto de 0.
6.
Alternativa A: Incorrecta. Se determina la pendiente efectuando incorrectamente el cuociente entre
la diferencia de las abscisas y la diferencia de las ordenadas.
Alternativa B. Incorrecta. Se determina la pendiente efectuando incorrectamente el cuociente entre
la diferencia de las abscisas y la diferencia de las ordenadas.
Alternativa C. Incorrecta. Al aplicarse la fórmula para determinar la pendiente, en vez de restar los
valores, estos se suman.
42
Alternativa D: CORRECTA. Se calcula la pendiente m 
, luego al resolver y simplificar se
8 6
obtiene que m = -3/7
Alternativa E: Incorrecta. La resta se efectúa con errores de signos.
7.
Alternativa A: CORRECTA. Para que el punto (4,-3) sea de la recta debe satisfacerla, entonces se
reemplaza en la ecuación, y resulta 4K + 3 = -2, de donde K = -5/4.
Alternativa B. Incorrecta. Al reemplazar se confunden los valores x e y, dando que –3K – 4 = -2, de
donde K = -2/3.
Alternativa C. Incorrecta. Se reemplaza el par, pero luego se comete un error algebraico grave al
resolver 4K + 3 como 7 K
Alternativa D: Incorrecta. Al reemplazar, un error de signo lleva a obtener que K = 1/4.
Alternativa E: Incorrecta. Se reemplaza K por el primer valor del par ordenado, entonces K = 4.
8.
Alternativa A: CORRECTA. Para que las rectas sean paralelas, las pendientes deben ser iguales, o
sea K = 2.
Alternativa B. Incorrecta. Se igualan los coeficientes de posición lo que no corresponde para
determinar si las rectas son paralelas. Luego se despeja en forma incorrecta.
Alternativa C. Incorrecta. Se igualan los coeficientes de posición lo que no corresponde para
determinar si las rectas son paralelas.
Alternativa D: Incorrecta. Se igualan las pendientes, pero luego se despeja mal.
Alternativa E: Incorrecta. Se considera en forma equivocada que los coeficientes de la primera
ecuación deben ser iguales.
9.
Alternativa A: Incorrecta. Se igualan los coeficientes de posición. Esto no permite definir si las
rectas son paralelas o paralelas.
Alternativa B. CORRECTA. Dos rectas son paralelas si el producto de sus pendientes es –1.
Entonces K(-2) = -1, de donde K = 1/2.
Alternativa C. Incorrecta. Se plantea que K(-2) = 1. Entonces K = -1/2.
Alternativa D: Incorrecta. Se igualan los coeficientes de posición, los cuales no determinan rectas
perpendiculares.
Alternativa E: Incorrecta. Que K = -2, determina rectas paralelas y no perpendiculares.
10.
Alternativa A: Incorrecta. Si se despeja y, se puede ver claramente que el coeficiente de posición
no corresponde a 4.
Alternativa B. Incorrecta. Se despeja y, pero luego se determina la pendiente, en vez del
coeficiente de posición.
Alternativa C. Incorrecta. Se piensa en este valor ya que se sabe que el coeficiente de posición no
va con ninguna incógnita, pero eso es cuando y está de la forma y = mx + n.
Alternativa D: Incorrecta. Se piensa en -3, el coeficiente de la y, como el coeficiente de posición, lo
cual no es correcto de acuerdo a la definición de él.
4x  5
Alternativa E: CORRECTA. Al despejar y se obtiene y 
donde se verifica que el coeficiente
3
de posición es –5/3.