PPT-TRANSF_LINEALES_RV.pdf

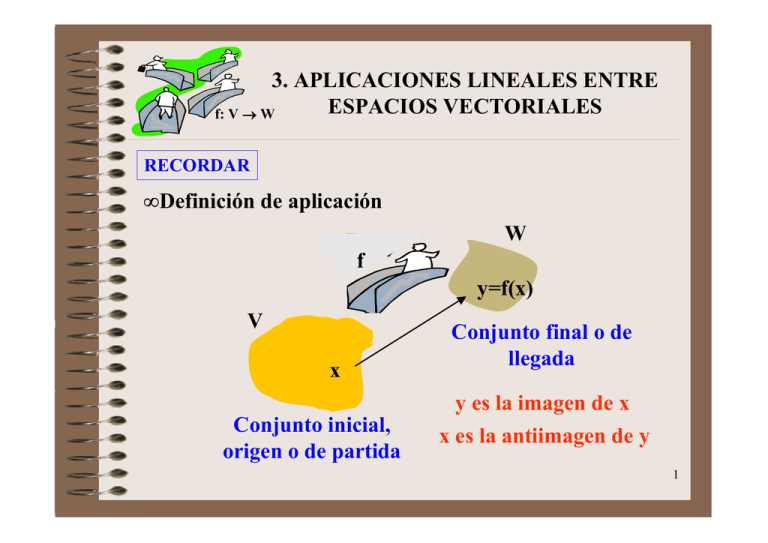
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
RECORDAR
• Definición de aplicación
W
f
y=f(x)
V
x
Conjunto inicial,
origen o de partida
Conjunto final o de
llegada
y es la imagen de x
x es la antiimagen de y
1
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
• Conjunto Imagen de una aplicación
V
W
u
v
y
z w
Im(f)
• Aplicación inyectiva: no hay dos vectores de V con la
misma imagen
W
V
u
y
v
No inyectiva
2
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
• Aplicación sobreyectiva: el conjunto imagen coincide
con el conjunto final
W
V u
y
v
z w
No sobreyectiva
• Aplicación biyectiva: inyectiva + sobreyectiva
3
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
3.1. DEFINICIÓN. IMAGEN Y NÚCLEO. PROPIEDADES.
V
u
v
αu+ βv
W
f(u)
f(v)
αf(u)+ βf(v)
f lineal ⇔ f(α
αu+ βv) = αf(u)+ βf(v) , ∀ α, β ∈ ℜ, ∀ u, v ∈ V
f(α
α1u1+ α2u2+ ... + αnun) = α1f(u1)+ α2f(u2)+ ... αnf(un)
f lineal u homomorfismo
f endomorfismo si V = W
4
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejemplos:
1) f : ℜ2 → ℜ2 tal que f(x1, x2) = (x1+ 2x2, x2 + 1), NO es
lineal.
Sean u = (1, 0), v = (0, 1)
f(u) = (1, 1)
f(v) = (2, 2)
f(u+ v) = f(1, 1) = (3, 2)
f(u)+ f(v) = (3, 3)
2) f : ℜ2 → ℜ2 tal que f(x1, x2) = (2x1, x1- x2), SÍ es lineal.
f (α (x1, x2) +β (x´1, x´2) ) = α f(x1, x2) + β f(x´1, x´2) ?
f(α
αx1+ βx´1, αx2+ βx´2)
α (2x1, x1- x2)+ β (2x´1, x´1- x´2)
( 2(ααx1+ βx´1) , αx1+ βx´1 – (ααx2+ βx´2) )
5
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
IMAGEN Y NÚCLEO DE UNA APLICACIÓN LINEAL
Sea f : V → W una aplicación lineal
Im(f) = { y ∈ W / ∃ x ∈ V verificando que f(x) = y }
N(f) = { x ∈ V / f(x) = θW }
f
V
N(f)
W
Im(f)
θ
N(f) e Im(f) son s.e.v de V y W respectivamente
6
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejemplo: dada la aplicación lineal f : ℜ3 → ℜ2 tal que
f(x1, x2 , x3) = (x1 + x3, x2- x3)
a) Hallar N(f) dando su dimensión y una base
b) Idem para Im(f). ¿Es f sobreyectiva? ¿Es f inyectiva?
a)
N(f ) = {( x1 , x 2 , x 3 ) / f ( x1 , x 2 , x 3 ) = (0,0)}
N(f ) = {( x1 , x 2 , x 3 ) / x1 + x 3 = 0, x 2 − x 3 = 0}
1 0 1 
dim N(f ) = 3 − rg
=1
 0 1 − 1
N(f) = {(-x3, x3, x3)}
B N ( f ) = {( −1, 1, 1)}
7
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
b)
Im(f ) = {( y 1 , y 2 ) ∈ ℜ 2 / ∃ ( x 1 , x 2 , x 3 ) ∈ ℜ 3 tal que f ( x 1 , x 2 , x 3 ) = ( y 1 , y 2 )}
y 1 = x1 + x 3 

2
3
Im(f ) = ( y 1 , y 2 ) ∈ ℜ / ∃ ( x1 , x 2 , x 3 ) ∈ ℜ tal que

y
x
x
=
−

2
2
3
 y1 
 1
 0
 1 
  = x1   + x 2   + x 3  
 0
 1
 − 1
 y2 
Im(f) = < (1,0), (0,1), (1,-1) >
dim Im(f) = 2
Im(f) = ℜ2
f es
sobreyectiva
8
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
PROPIEDADES DE UNA APLICACIÓN LINEAL
PROPIEDAD 1: f(θ
θV) = θW
PROPIEDAD 2: Si {v1, v2,..., vn} es un s.g. de V, entonces
{f(v1), f(v2),..., f(vn)} es un s.g. de Im(f).
Ejercicio: se considera la aplicación lineal f : ℜ4 → ℜ3
dada por:
f(x1, x2 , x3 , x4) = (x1 + x2 - x3, x1 + x2 + x3 +2x4, x3+ x4)
a) Hallar un s.g. y una base de Im(f)
b) Hallar las ecs. implícitas de Im(f)
c) Hallar la dimensión , base y ecs. implícitas de N(f)
9
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
a) La Bc es un s.g. del espacio inicial. Las imágenes de
sus vectores son un s.g. de Im(f)
f(1, 0, 0, 0) = (1, 1, 0)
f(0, 1, 0, 0) = (1, 1, 0)
f(0, 0, 1, 0) = (-1, 1, 1)
f(0, 0, 0, 1) = (0, 2, 1)
Son un s.g. de Im(f)
Im(f) = < (1, 1, 0), (1, 1, 0), (-1, 1, 1), (0, 2, 1) >
 1 1 − 1 0


dim Im(f ) = rg 1 1 1 2  = 2
 0 0 1 1


Base Im(f) = { (1,1,0), (-1,1,1) }
10
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
b)
Nº de ecuaciones implícitas = 3- 2 = 1
( y 1 , y 2 , y 3 ) = α(1,1,0) + β( −1,1,1)
y1 = α − β 

y 2 = α + β

y3 = β

Ecs. Paramétricas
y 1 − y 2 + 2y 3 = 0
Ec. Implícita de Im(f)
c) N(f ) = {( x1 , x 2 , x 3 , x 4 ) ∈ ℜ 4 / f ( x1 , x 2 , x 3 , x 4 ) = ( 0,0,0)}
x1 + x 2 − x 3 = 0 



N(f ) = ( x1 , x 2 , x 3 , x 4 ) ∈ ℜ 4 / x1 + x 2 + x 3 + 2x 4 = 0


x
+
x
=
0


3
4
11
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
 1 1 − 1 0


dim N(f ) = 4 − rg 1 1 1 2  = 2
 0 0 1 1


 x1 + x 2 − x 3 = 0
Ecs. Implícitas de N(f)
N(f ) ≡ 
 x1 + x 2 + x 3 + 2x 4 = 0
 x 2 − x 3 = − x1

 x 2 + x 3 = − x 1 − 2x 4
 x 2 = − x1 − x 4

 x3 = − x4
N(f ) = {( x1 ,− x1 − x 4 ,− x 4 , x 4 )} = { x1 (1,−1,0,0) + x 4 (0,−1,−1,1)}
Base N(f) = { (1, -1, 0, 0), (0, -1, -1, 1) }
12
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
PROPIEDAD 3: f es inyectiva ⇔ N(f) = {θ
θV}
Ejercicio: se considera la aplicación f : M2x2 → M2x1 dada
por:
a b b
f
= 
 c d  c 
a) Probar que es lineal
b) ¿Es f inyectiva?
c) Hallar un s.g. y una base del Im(f). ¿Es f sobreyectiva?
13
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
a)
a b
 a´ b´  ?  a b 
 a´ b´ 
 +β
 = αf
 + βf

f α
β
 c d
 c´ d´ 
 c d
 c´ d´ 
 αa + β a´ αb + β b´ 
f

 αc + β c´ αd + β d´ 
 αb + β b´ 


 αc + β c´ 
 b   b´ 
α  + β 
 c   c´ 
f es lineal
14
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
b)
 0 0  
¿ N(f ) = 
 ?
 0 0  
 a b   a b   0  
N ( f ) = 
 /f
 =  
 c d   c d   0  
 a b   b   0 
N(f ) = 
 /   =  
 c d   c   0 
 a 0  
N(f ) = 

f no es
 0 d   inyectiva
15
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
c)
 1 0  0
f
= 
 0 0  0
 0 0  0
f
= 
 1 0  1
 0 1  1
f
= 
 0 0  0
 0 0  0
f
= 
 0 1  0
 1  0
Im(f ) =  ,  
 0  1
Im(f) = M2x1
dim Im(f) = 2 = dim M2x1
f es sobreyectiva
16
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
PROPIEDAD 4: dim V = dim N(f)+ dim Im(f)
PROPIEDAD 5: f y g lineales ⇒ también lo son f ± g y f ° g.
Ejercicio: se considera el endomorfismo f : ℜ3 → ℜ3 dado
por: f(x1, x2 , x3 ) = ( x2 + x3, -2x1 + x2, -2x1+2x2+ x3)
a) Hallar un s.g. , la dimensión y una base de Im(f)
b) Hallar las ecs. implícitas de Im(f)
c) Hallar la dimensión , base y ecs. implícitas de N(f)
d) ¿Es f inyectiva? ¿Y sobreyectiva?
e) ¿Es ℜ3 = N(f) ⊕ Im(f)?
17
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
3.2. MATRIZ ASOCIADA A UNA APLICACIÓN LINEAL.
Sea V
dim V = n
B1 base de V
f
W lineal
dim W = m
B2 base de W
x∈V
f(x)= y ∈ W
x = ( x1 , x 2 ,..., x n )B1
y = ( y 1 , y 2 ,..., y m )B 2
¿Cómo relacionar matricialmente las coordenadas
del vector x respecto a B1 con las coordenadas de su
imagen y respecto a B2 ?
18
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
La relación matricial entre las coordenadas de un vector
y las de su imagen respecto a las bases canónicas
respectivas, puede establecerse fácilmente si conocemos
la expresión analítica de la aplicación.
Ejemplo: Sea la aplicación f : ℜ2 → ℜ3 dada por:
f(x1, x2 ) = (-x1 + x2, 2x1 – x2, - x2)
(x1, x2 ) ∈ ℜ2
(y1, y2 , y3 ) ∈ ℜ3 tal que:
y 1 = − x1 + x 2
y 2 = 2 x1 − x 2
y 3 = − x2
19
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
 y1   − 1 1 
  
 x1 
 y 2  =  2 − 1  
 y   0 − 1  x 2 Bc2

 3 Bc3 
Matriz de f respecto a las bases
canónicas respectivas
f(1,0) f(0,1)
Si las bases que se consideran en el espacio inicial y
final son bases cualesquiera, necesitamos conocer
cierta información sobre ellas.
20
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejercicios:
1) Sean B1 = {u1, u2, u3} y B2 = {v1, v2} dos bases de
ℜ3 y ℜ2 respectivamente, y f : ℜ3 → ℜ2 tal que:
f(u1) = 2v1- v2
f (u1 ) = ( 2,−1)B 2
f(u2) = -v1+ v2
f (u 2 ) = ( −1,1)B 2
f(u3) = -v2
f (u 3 ) = (0,−1)B 2
Sea x ∈ ℜ3 tal que x = (x1, x2, x3)B1. Hallar la
expresión matricial de f respecto a B1 y B2
Exp. que permite relacionar las coordenadas de x resp. a
B1, con las coordenadas de f(x) respecto a B2, (y1, y2)B2 21
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
x = ( x 1 , x 2 , x 3 ) B1
⇔ x = x 1u 1 + x 2 u 2 + x 3 u 3
f ( x ) = f ( x 1 u 1 + x 2 u 2 + x 3 u 3 ) = x 1f ( u 1 ) + x 2 f ( u 2 ) + x 3 f ( u 3 )
f es lineal
= x1 ( 2 v 1 − v 2 ) + x 2 ( − v 1 + v 2 ) + x 3 ( − v 2 ) =
= ( 2x1 − x 2 ) v 1 + ( − x1 + x 2 − x 3 ) v 2
Las coordenadas de f(x) respecto a B2, (y1, y2)B2, son:
y 1 = 2x 1 − x 2
y 2 = − x1 + x 2 − x 3
22
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
 x1 
Expresión
y 
 2 − 1 0  
matricial de f  1  = 
 x 2 
respecto a B1 y  y 2  B
 − 1 1 − 1  
2
 x 3  B1
B2
Matriz asociada a f
respecto a B1 y B2
Coord. de f(u1) respecto a B2
Coord. de f(u2) respecto a B2
Coord. de f(u3) respecto a B2
Datos
necesarios
para hallar la
matriz de f
23
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
2) Sea la aplicación lineal f : ℜ3 → ℜ2 dada
por: f(x1, x2 , x3 ) = (-2x1 + x2, 3x1 + x2 + x3)
a) Hallar la expresión matricial de f respecto a las bases:
B1 = { (-1,1,0), (0,1,0), (1,0,1) } de ℜ3 y B2 = {(1,2), (0,1)}
de ℜ2.
b) Hallar la expresión matricial de f respecto a las bases
canónicas respectivas.
24
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
a)
 y1 

  =
 y 2 B2 
 x1 
 
 x 2 
 
 x 3  B1
Coord. de f(-1,1,0) respecto a B2
Coord. de f(0,1,0) respecto a B2
Coord. de f(1,0,1) respecto a B2
Los datos no los da el problema, tenemos que hallarlos
25
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
f(-1,1,0) = (3, -2)
f(0,1,0) = (1, 1)
f(1,0,1) = (-2, 4)
= α (1, 2)+ β (0, 1)
 3=α

 − 2 = 2α + β
f ( −1,1,0) = ( 3,−8)B 2
 y1 
 
 y 2 B2
1 = α

1 = 2α + β
− 2 = α

 4 = 2α + β
f (0,1,0) = (1,−1)B 2
f (1,0,1) = ( −2,8)B 2
 x1 
1 − 2  
 3
=
 x 2 
 − 8 − 1 8  
 x 3  B1
26
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
 y1 
 
 y 2  Bc2
b)
 x1 
− 2 1 0  
=
 x 2 
 3 1 1  
 x 3  Bc3
1ª Forma: como a)
Coord. de f(1,0,0) = (-2, 3) respecto a Bc2
Coord. de f(0,1,0) = (1, 1) respecto a Bc2
Coord. de f(0,0,1) = (0, 1) respecto a Bc2
2ª Forma:
directamente
(x1, x2 , x3 )
(y1, y2 ) tal que:
y 1 = −2x 1 + x 2
y 2 = 3x 1 + x 2 + x 3
27
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
3) Sea el endomorfismo f : ℜ3 → ℜ3 dado por:
f(x1, x2 , x3 ) = (-x1 + x2, 3x1 + x2 + x3 , x3 )
a) Hallar la expresión matricial de f respecto a la base
canónica.
b) Hallar la expresión matricial de f respecto a la base
B = { (1,-1,0), (0,-1,0), (-2,-1,1) } .
a)
 y1 
− 1 1 0 x1 
 

 
 y 2  = 3 1 1 x 2 

 x 
y 
0
0
1
 3  B c
 3  Bc 
28
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
b)
 y 1  − 2 − 1
 

 y 2  = 0
2

y 
0
 3  B 0
f(1,-1,0) = (-2, 2, 0)
f(0,-1,0) = (-1, -1, 0)
f(-2,-1,1) = (1, -6, 1)
3 x1 
2 x 2 
 
1 x 3  B
= α (1,-1,0)+ β (0, -1,0)+ γ (-2,-1,1)
Entre las matrices de los apartados a) y b) de los
ejercicios 2) y 3), existe una relación, puesto que
representan a la misma aplicación lineal.
29
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
RELACIÓN ENTRE LAS MATRICES ASOCIADAS A UNA
MISMA APLICACIÓN LINEAL RESPECTO DE DISTINTAS
BASES
f:V
A
W
B1
Matriz de
cambio de T1
base en V
C1
B2
A´
T2
Matriz de
cambio de
base en W
C2
A´= T A T1
−1
2
30
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejemplos:
1) El ejemplo 2 anterior
A
3
ℜ2
f:ℜ
B1
T1
B
3
c
−1 0 1 


T1 =  1 1 − 1 
 0 0 1 


B2
1 − 2
 3
A=

− 8 −1 8 
T2
A´
B c2
 1 0
T =

 2 1
 − 2 1 0
A´= 

 3 1 1
A´= T2−1 A T1
−1
2
31
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
2) El ejemplo 3 anterior
f:
ℜ3
A
B c3
ℜ3
B c3
P
P
B
A´
0 − 2
 1


P =  − 1 − 1 − 1

 0
0
1


B
 − 1 1 0


A =  3 1 1
 0 0 1


 − 2 − 1 3


A´=  0
2 2

0 1 
 0
A´= P −1 A P
32
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
PROPIEDADES DE LA
APLICACIÓN LINEAL
MATRIZ
ASOCIADA
A
UNA
PROPIEDAD 1: dim Im(f) = rg A
A
f:V
W
B1={u1, ..., un}
.


A =
.

.

f (u 1 ) B 2
f (u 2 ) B 2





f (u n ) B 2
B2={v1,..., vm}
Im(f ) =< f (u 1 ) B 2 ,..., f (u n ) B 2 >
dim Im(f) = rg A
33
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejercicio:
La matriz asociada a un endomorfismo f de ℜ3
respecto a la base canónica es:
 − 1 0 2


A =  1 1 0
 0 1 2


a) Escribir la expresión matricial y analítica de f
b) Hallar la dimensión y una base de Im(f)
c) Hallar la dimensión y las ecuaciones implícitas de
N(f)
34
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
a)
 y1 
 − 1 0 2  x 1 
 

 
 y 2  =  1 1 0  x 2 
 0 1 2  x 
y 
 3  B
 3 B 
c
c
f(x1, x2 , x3 ) = (-x1 + 2x3, x1 + x2 , x2 + 2x3 )
b) dim Im(f) = rg A = 2
B Im( f ) = {( −1,1,0), (0,1,1)}
c) dim N(f) = dim V- dim Im(f) = 1
 0 
 − 1 0 2  x1 

 
 
 − x1 + 2x 3 = 0
N(f ) ≡  0  =  1 1 0  x 2 
N(f ) ≡ 
 0 1 2  x 
 0 
 x1 + x 2 = 0 35
 3  B
  B 
c
c
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
PROPIEDAD 2: si f es lineal con matriz asociada A,
entonces αf es lineal con matriz asociada αA.
PROPIEDAD 3: si f y g son lineales con matrices asociadas
A y B, respectivamente, entonces f ± g y f ° g son lineales*
con matrices asociadas A ± B y AB, respectivamente.
(*siempre que dicha composición pueda efectuarse)
36
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
Ejercicio: Se consideran las aplicaciones lineales
f : ℜ3 → ℜ2 y g: ℜ2→ ℜ4 dadas por:
f(x1, x2 , x3 ) = (-x1 + x2, 3x1 + x2 + x3)
g(1, 1) = (-1, 2, 0, 1)
g(-1, 0) = (2, -3, 0, 0)
a) Hallar las matrices A y B asociadas a f y g,
respectivamente, respecto a las bases canónicas en
los espacios inicial y final.
b) Hallar, si es posible, las matrices asociadas a las
37
aplicaciones f ° g y g ° f.
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
a)
 − 1 1 0
A=

 3 1 1
Sea Bc2 = {e1, e2}
Sabemos que:
g(e1+e2) = (-1, 2, 0, 1)
g es lineal
g(e1)+ g(e2) = (-1, 2, 0, 1)
g(e2) = (1, -1, 0, 1)
− 2 1 


 3 − 1
B=
0 0


 0 1 4x 2
g(1,0) g(0,1)
respecto a Bc4
g(-e1) = (2, -3, 0, 0)
-g(e1) = (2, -3, 0, 0)
g(e1) = (-2, 3, 0, 0)
38
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
b) f ° g no puede efectuarse, pues no existe AB
B4x2 ⋅ A2x3
g°f
g ° f : ℜ3 → ℜ4
 5 −1 1 


 − 6 2 − 1
=
0
0
0 


1
1 
 3
39
3. APLICACIONES LINEALES ENTRE
ESPACIOS VECTORIALES
f: V → W
ENDOMORFISMO INVERSO
Sea f: V → V un endomorfismo, con matriz asociada
A, tal que existe A-1. Llamamos endomorfismo inverso
de f, a la aplicación lineal f-1 : V → V cuya matriz
asociada es A-1.
Ejercicio:
Estudiar si tiene inverso el endomorfismo f de ℜ3 cuya
matriz asociada respecto a la base canónica es:
 − 1 0 2


A =  1 1 0
 0 1 2


40
FIN DEL TEMA !