Ejerciciosdela Unidad1.1

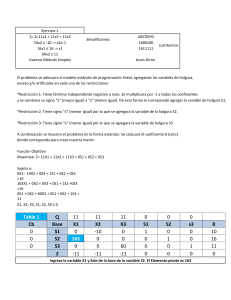
[MÉTODO SIMPLEX]
CATEDRATICO, ING:
DARIO RUIZ
ALUMNA:
MIRNA TREJO
AGOSTO/3/2011
PROBLEMAS
EN ESTE PARCIAL HEMOS DESARROLLADO EL MÉTODO
SIMPLEX CON SUS VARIABLES DE HOLGURA, ADEMAS
DE DETERMINAR EL MAXIMO U MÍNIMO DE LA
FUNCION.
Ejercicios.
Para cada uno de los siguientes ejercicios formule el modelo de programación
lineal.
La Swelte Glove Company fabrica y vende dos productos. Dicha compañía obtiene
una ganancia de $12 por cada unidad que vende de su producto 1, y de $4 por
cada unidad de producto 2. Los requerimientos en términos de horas de trabajo
para la fabricación de estos productos en los tres departamentos de producción se
enumeran de manera resumida en la siguiente tabla. Los supervisores en estos
departamentos han estimado que tendrán las siguientes disponibilidades de horas
de trabajo durante el próximo mes: 800 horas en el departamento 1, 600 horas en
el departamento 2 y 2000 horas en el departamento 3. Suponiendo que la
compañía esté interesada en maximizar las ganancias, desarrolle usted el modelo
de programación lineal correspondiente.
Requerimiento de horas de trabajo
Departamento 1
Producto 1
Producto 2
1
1
2
2
1
3
3
2
3
Función objetivo
Maximizar Z=12x+4y (Ganancias)
Restricciones:
X+ 2y≤ 800 (Horas de trabajo del departamento 1)
X+ 3y≤ 600 (Horas de trabajo del departamento 2)
2x+ 3y≤2000 (Horas de trabajo del departamento 3)
Modelo de P.L
Modelo estándar (igualdades)
Maximizar z= 12x+4y---- 12x +4y+ 0S1+ 0S2+ 0S3
Sujeto a: x +2y≤800 ----- x+2y+S1+0S2+0S3=800
X+ 3y≤600 ----- x+3y+0S1+S2+0S3=600
2x+3y≤2000----- 2x+3y+0S1+0S2+S3=2000
X,y ≥0
x,y, S1,S2,S3≥0
C
12
4
0
0
0
X
Y
S1
S2
S3
0
S1
1
2
1
0
0
800
0
S2
1
3
0
1
0
600
0
S3
2
3
0
0
1
2000
0
0
0
0
0
0
Z
c-z
12
4
0
0
0
Paso 1: Determinar el renglón Z. Se multiplica la columna C por la columna X y se
suman los resultados, y así sucesivamente con las demás columnas.
Paso 2: determinar renglón c-z. al renglón restar el renglón z
Paso 3: Determinar la variable que entra (columna). Del renglón c-z. Del renglón cz escoger el número más positivo
Paso 4: Determinar la variable que sale (fila). Dividir la columna de resultados
entre la columna de la variable que entra
800/1=800
600/1=600
200/2=1000
Y se escoge la menor división
Paso 5: Determinar el elemento clave. Ese elemento siempre tiene que ser 1, si no
es 1 convertirlo en 1.
Paso 6: convertir a 0 todos los demás elementos de la columna clave
C
R1
R2
R3
0
12
0
S1
x
S3
Z
c-z
12
X
0
1
0
12
0
4
Y
1
3
3
36
-32
0
S1
1
1
0
0
0
0
S2
1
0
-2
12
-12
0
S3
0
0
1
0
0
200
600
800
7200
R2(-1)+r1
R2(-2)+r3
No se continúa con las operaciones porque en el renglón c-z no aparecen
números positivos.
R2 (-1)+R1=1(-1)+1=0
R2 (-1)+R1= (1)+2
R2 (-1)+R1=1(-1)+1
R2 (-2)+R3=1(-2)+2=0
R2 (-2)+ R3=3(-2)+3=3
R2 (-2)+R3=0(-2)+0=0
R2 (-2)+R3=1(-2)+0=-2
R2 (-2)+R3=0(-2)+1=1
R2 (-2)+R3=600(-2)+2000=800
Maximizar z= 12x+4y
Restricciones:
X+ 2y≤ 800
X+ 3y≤600
2x+ 3y≤2000
X,y≥0
X+ 2y≤ 800
600+2(0) ≤800
600≤800 Restricción inactiva horas de trabajo del dpto.1
X+3y≤600
600+3(0) ≤600
600≤600 Restricción activa
2x+3≤2000
2(600)+3(0) ≤2000
1200≤2000 Restricción inactiva horas de retrabajo del dpto.3 no utilizadas.
Conclusión: La empresa Swelte Glove obtendrá una ganancia de $7,200 de la
venta y fabricación del producto 1(x) de los cuales se venderán 600 unidades y
cero unidades del producto 2(y). Utilizando 3 dptos.para la fabricación de los
productos utilizando todas las horas del dpto.2. No se utilizaron todas las horas del
dpto. 1 y 3.
Wood Walker es propietario de un pequeño taller de fabricación de muebles. En
ese taller fabrica tres tipos diferentes de mesas: A, B y C. Con cada mesa, se
requiere determinado tiempo para cortar las partes que la constituyen,
ensamblarlas y pintar la pieza terminada. Wood podrá vender todas las mesas que
consiga fabricar. Además el modelo C puede venderse sin pintar. Wood emplea a
varias personas, las cuales trabajan en turnos parciales, por lo cual el tiempo
disponible para realizar cada una de estas actividades es variable de uno a otro
mes. A partir de los datos siguientes, formule usted un modelo de programación
lineal que ayude a Wood a determinar la mezcla de productos que le permitirá
maximizar sus ganancias en el próximo mes.
Modelo
Corte(hrs)
Montaje(hrs)
Pintura(hrs)
Ganancia por mes
A
3
4
5
25
B
1
2
5
20
C
4
5
4
50
C sin pintar
4
5
0
30
Capacidad
150
200
300
1. Formacion del problema.
a) Determinar el objeto del problema.
Max o min. Las ganancias.
b) Definir las variables del problema.
Z= Ganancias
X1=Modelo de mesa A
c1= $25
X2=Modelo de mesa B
c2= $20
X3=Modelo de mesa C
c3= $50
X4=Modelo de la mesa C sin Pintar
C4= $30.
Z= 25x1+20x2+50x3+30x4
c) Establecer las restricciones del problema.
1. Corte (hrs)
Capacidad= 150
Función objetivo
Maximizar Z=25x1+20x2+50x3+30x4 (Ganancias del prox. mes)
Restricciones:
3X1+X2+4X3+4X4≤150 (corte, montaje, pintura y sin pintura (hrs))
4X1+2X2+5X3+5X4≤200 (corte, montaje, pintura y sin pintura (hrs))
5X1+5X2+4X3+0X4≤300 (corte, montaje, pintura y sin pintura (hrs))
Modelo de P.L
Modelo estándar (igualdades)
Maximizar z=25x1+20x2+50x3+30x4
Sujeto a: 3X1+X2+4X3+4X4≤150
25x1+20x2+50x3+30x4+0S1+0S2+0S3
3x1+x2+4x3+4x4+1S1+0S2+0S3=150
4X1+2X2+5X3+5X4≤200
4X1+2X2+5X3+5X4+0S1+1S2+0S3=200
5X1+5X2+4X3+0X4≤300
5X1+5X2+4X3+0X4+0S1+0S2+1S3=300
X1, x2, x3, x4≥0
C
25
X1, x2, x3, x4, 0S1, 0S2, 0S3≥0
20
50
30
0
0
0
X1
X2
X3
X4
S1
S2
S3
0
S1
3
1
4
4
1
0
0
150
0
S2
4
2
5
5
0
1
0
200
0
S3
5
5
4
0
0
0
1
300
Z
0
0
0
0
0
0
0
0
C-Z
25
20
50
30
0
0
0
C
25
20
30
0
0
0
0
X1
X2
X3
X4
S1
S2
S3
50
X3
¾
0
1
1
1/4
0
0
37 ½
0
S2
¼
2
0
0
-1 1/4
1
0
12 ½
0
S3
2
5
0
-4
-1
0
1
150
Z
37 ½
0
50
50
12 1/2
0
0
1875
C-Z
-12 ½
20
-20
-50
-12 1/2
0
0
25
20
30
0
0
0
0
X1
X2
X3
X4
S1
S2
S3
1
1/4
0
0
37 ½
C
50
X3
¾
0
1
20
X2
1/8
1
0
0
-5/8
1/2
0
6¼
0
S3
1 3/8
0
0
-4
2 1/8
-2 1/2
1
118 ¾
Z
40
20
50
50
0
10
0
C-Z
-15
0
-20
-50
0
-10
0
2000
No se continúa con las operaciones porque en el renglón c-z no aparecen
números positivos.
Maximizar Z=25x1+20x2+50x3+30x4
Sujeto a: 3X1+0X2+4X3+4X4≤150
3(0)+0(6.25)+4(37.5)≤150
150≥150 Restriccion activa (corte,
montaje, pintura y sin pintura (hrs))
4X1+2X2+5X3+5X4≤200
4(0)+2(6.25)+5(37.5)+5(0)≤200
200≤200 Restriccion inactiva (corte,
5X1+5X2+4X3+0X4≤300
5(0)+5(6.25)+5(37.5)+0(0) ≤300
montaje, pintura y sin pintura (hrs))
218.75≤300 Restriccion activa (corte,
montaje, pintura y sin pintura (hrs))
X1, x2, x3, x4≥0
Conclusión: La compañía Wood Walker obtendrá una ganancia de $2000 la mayor
parte del montaje y de pintura …
Cada una de las tres maquinas fábrica dos productos. Para elaborar una libra de
cada producto se requiere una cantidad determinada de horas de trabajo en cada
maquina, como se indica en la siguiente tabla. Las horas disponibles en las
maquinas 1, 2 y 3 son 10, 16 y 12 respectivamente. Las contribuciones a las
ganancias correspondientes a cada libra de los productos 1 y 2 son $4 y $3,
respectivamente.
Defina las variables de decisión, formule esté problema como un programa lineal
para la maximización de la ganancia.
Requerimiento de horas/maquina
Maquina
Producto 1
Producto 2
1
3
2
2
1
4
3
5
3
Función objetivo
Maximizar Z=4x+5y (Ganancias)
Restricciones:
3x+2y≤10 (Horas de trabajo en maquina 1)
X+4y≤16 (Horas de trabajo en maquina 2)
5x+3y≤12 (Horas de trabajo en maquina 3)
Modelo de P.L
Modelo estándar (igualdades)
Maximizar Z=4x+5y
4x+5y+0S1+0S2+0S3
Sujeto a: 3x+2y≤10
3x+2y+S1+0S2+0S3=10
X+4Y≤16
x+4y+0S1+S2+0S3=16
5X+3Y≤12
5X+3y+0S1+0S2+S3=12
X,y ≥0
x,y, S1,S2,S3≥0
C
4
5
0
0
0
X
Y
S1
S2
S3
0
S1
3
2
1
0
0
10
0
S2
1
4
0
1
0
16
0
S3
5
3
0
0
1
12
Z
0
0
0
0
0
C-Z
4
5
0
0
0
C
0
4
5
0
0
0
X
Y
S1
S2
S3
0
S1
-1/3
0
1
0
-2/3
2
0
S2
-5 2/3
0
0
1
-1 1/3
0
5
Y
1 2/3
1
0
0
1/3
4
Z
8 1/3
5
0
0
1 2/3
20
C-Z
-4 1/3
0
0
0
-1 2/3
No se continúa con las operaciones porque en el renglón c-z no aparecen
números positivos.
Maximizar Z=4x+5y
Sujeto a: 3x+2y≤10
3(0)+ 2(4)≤10
8≤10 Restriccion Inactiva (Horas de trabajo en maq. 1) no usada.
X+4Y≤16
(0)+ 4(4) ≤16
16≤16 Restriccion Activa (Horas de trabajo de la maq. 2)
5X+3Y≤12
5(0)+3(4) ≤12
12≤12 Restriccion Activa (Horas de trabajo de la maq. 3)
X,y ≥0
Conclusión: Cada una de las maq. 2 y 3 aportaron horas de trabajo, la maquina 1
no se uso. Y se obtuvo una ganancia de $20. Por c/maq.
RMC es una pequeña empresa que fabrica una variedad de productos basados en
sustancias químicas. En un proceso de producción particular, se emplean tres
materias primas para producir dos productos: un aditivo para combustible y una
base para solvente. El aditivo para combustible se vende a compañías petroleras y
se usa en la producción de gasolina y combustibles relacionados. La base para
solvente se vende a una variedad de empresas químicas y se emplea en
productos para limpieza en el hogar e industriales. Las tres materias primas se
mezclan para fabricar el aditivo para combustible y la base para el solvente, tal
como se muestra a continuación:
Producto
Material 1
Aditivo para combustible
Base para solvente
0.4
0.5
Material 2
Material 3
0.2
0.6
0.3
Ésta nos muestra que una tonelada de aditivo para combustible es una mezcla de
0.4 toneladas del material 1 y 0.6 toneladas del material 3. Una tonelada de la
base para solvente es una mezcla de 0.5 toneladas del material 1, 0.2 toneladas
del material 2 y 0.3 toneladas del material 3.
La producción de RMC esta restringida por una disponibilidad limitada de las tres
materias primas. Para el periodo de producción actual, RMC tiene disponibles las
siguientes cantidades de materia prima:
Material
Cantidad disponible para la producción
1
20 toneladas
2
5 toneladas
3
21 toneladas
Debido a los desechos y a la naturaleza del proceso de producción, los materiales
que no se lleguen a usar en una corrida de producción no se pueden almacenar
para las subsiguientes, son inútiles y deben desecharse.
El departamento de contabilidad analizó las cifras de producción, asignó todos los
costos relevantes y llegó a precios que, para ambos productos, producirían una
contribución a la utilidad de $ 40 por cada tonelada de aditivo para combustible
producida y $ 30 para cada tonelada producida de base para solvente. Ahora
usaremos la programación lineal para determinar la cantidad de aditivo para
combustible y la cantidad de base para solvente para producir a fin de maximizar
la contribución a la ganancia total.
Función objetivo
Maximizar Z=40X+30Y (Contribución a la ganancia)
Restricciones:
0.4x+0.5y≤20 (toneladas de material disponibles para la producción)
0x+0.2y≤5 (toneladas de material disponibles para la producción)
0.6x+0.3y≤21 (toneladas de material disponibles para la producción)
Modelo de P.L
Modelo estándar (igualdades)
Maximizar Z=40x+30y
40x+30y+0s1+0s2+0s3
Sujeto a: 0.4x+0.5y≤20
0.4x+0.5y+S1+0S2+0S3=20
0x+0.2y≤5
0.0x+0.2y+0S1+S2+0S3=5
0.6x+0.3y≤21
0.6x+0.3y+0S1+0S2+S3=21
X, y ≥0
x, y, S1, S2, S3≥0
C
40
30
X
Y
0
0
0
S1
S2
S3
0
S1
2/5
½
1
0
0
20
0
S2
0
1/5
0
1
0
5
0
S3
3/5
3/10
0
0
1
21
0
0
0
0
0
0
40
30
0
0
0
Z
C-Z
C
40
30
0
0
0
X
Y
S1
S2
S3
0
S1
0
3/10
1
0
-2/3
6
0
S2
0
1/5
0
1
0
5
0
S3
1
½
0
0
1 2/3
35
0
0
0
0
0
0
Z
C-Z
40
30
0
0
0
No se continúa con las operaciones porque ya están igualadas a uno y los demás
a cero.
Maximizar Z=40x+30y
Sujeto a: 0.4x+0.5y≤20
0.4(0)+0.5(0) ≤20
0≤20 Restriccion Inactiva (toneladas de material disponibles para la producción)
no usada.
0x+0.2y≤5
0(0)+0.2 (0) ≤5
0≤5 Restriccion Inactiva (toneladas de material disponibles para la producción)
no usada.
0.6x+0.3y≤21
0≤21 Restriccion Inactiva (toneladas de material disponibles para la producción)
no usada.
X, y ≥0
Conclusión: no se aplicaron las restricciones porque la empresa no se limita para
cumplir los requerimientos del cliente.
M & D Chemicals produce dos productos que se venden como materias primas a
compañías que fabrican jabones para baño y detergentes para ropa. Basado en
un análisis de los niveles de inventario actuales y la demanda potencial para el
mes siguiente, la gerencia de M & D ha especificado que la producción combinada
para los productos A y B debe ser en total al menos 350 galones. Por separado,
también debe satisfacerse un pedido de un cliente importante de 125 galones del
producto A. El producto A requiere dos horas de procesamiento por galón,
mientras el producto B requiere una hora de procesamiento por galón, y para el
siguiente mes se dispone de 600 horas de tiempo de procesamiento. El objetivo
de M & D es satisfacer estos requerimientos con un costo total de producción
mínimo. Los costos de producción son $2 por galón para el producto A y $3 por
galón para el producto B.
Función objetivo:
Minimizar z=2x+3y (costo total)
Restricciones:
X+y≥350 (jabones de baño y detergente para ropa)
X=125 (jabones de baño y detergente para ropa)
2x+y≤600 (jabones de baño y detergente para ropa)
Modelo de P.L
Modelo estándar (igualdades)
Minimizar z=2x+3y
2x+3y+MA1+MA2+0S1+0S2
Sujeto a: X+y≥350
x+y-S1+0S2+A1+0A2=350
X=125
x+0y+0S1+0S2+0A1+A2=125
2x+y≤600
2x+y+0S1+S2+0A1+0A2=600
X, y ≥0
S1, S2, A1, A2≥0
C
2
3
M
X
y
A1
M
0
0
A2
0S1
0S2
M
A1
1
1
-1
0
1
0
350
M
A2
1
0
0
0
0
1
125
0
S
2
1
0
1
0
0
600
Z
2M
M
-M
0
M
M
475M
C-Z
2-2M
3-M
2M
M
-M
-M
2
3
M
M
0
0
X
Y
S1
S2
C
A1
A2
M
A1
0
1
-1
0
1
-1
225
2
X
1
0
0
0
0
1
125
0
S
0
1
0
1
0
-2
350
Z
2
M
-M
0
M
-M+2
225M+250
C-Z
0
3-M
2M
M-0
-M
M-2
No se continua con las operaciones porque el valor +negativo ya tiene el elemento
clave igualado a uno y los que deben ser ceros ya son.
Minimizar z=2x+3y
Sujeto a: X+y≥350
X=125
125=125
2x+y≤600
2(125)+0≤600
250≤600
X, y ≥0