4.7 Cálculo de momentos, centros de masa y trabajo.

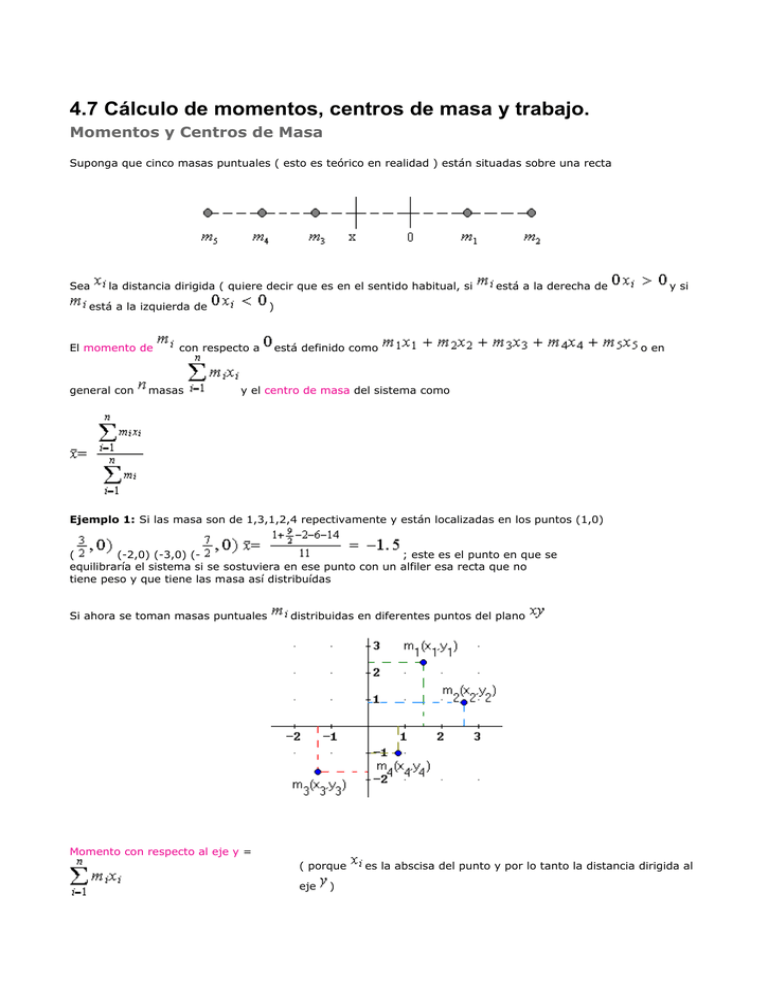
4.7 Cálculo de momentos, centros de masa y trabajo.
Momentos y Centros de Masa
Suponga que cinco masas puntuales ( esto es teórico en realidad ) están situadas sobre una recta
Sea
la distancia dirigida ( quiere decir que es en el sentido habitual, si
está a la izquierda de
El momento de
general con
y si
)
con respecto a
masas
está a la derecha de
está definido como
o en
y el centro de masa del sistema como
Ejemplo 1: Si las masa son de 1,3,1,2,4 repectivamente y están localizadas en los puntos (1,0)
(
(-2,0) (-3,0) (; este es el punto en que se
equilibraría el sistema si se sostuviera en ese punto con un alfiler esa recta que no
tiene peso y que tiene las masa así distribuídas
Si ahora se toman masas puntuales
distribuidas en diferentes puntos del plano
Momento con respecto al eje y =
( porque
eje
)
es la abscisa del punto y por lo tanto la distancia dirigida al
Momento con respecto al eje x
( porque
eje
=
=
(
es la ordenada del punto y por lo tanto la distancia dirigida al
)
=
es sel centro de masa del sistema
Ejemplo 2: masas de 2,2,1,3,1,4 gramos están localizadas respectivamente en los puntos (1,1)
(2,3) (4,6) (-3,1) (-2,-2) (-4,-1) . Encontrar el centro de masa del sistema
En el punto
se encuentra localizado el centro de masa de este sistema.
Este sería el punto donde se equilibraría, sostenido por un alfiler, el sistema suponiendo que las masas están
distribuidas sobre una lámina extremadamente delgada que no tiene peso.
CENTRO DE MASA DE UNA REGIÓN PLANA.
La región plana se va a tomar como una lámina bidimensional de densidad
( en g/cm
o kg/m
o lb/p
)
Si una región tiene un ejes de simetría, el centro de masa (si la densidad es uniforme ) estará sobre el o los ejes
de simetría: Así un circulo tendrá su centro de masa en el centro que es el punto de intersección de los diámetros,
un rectángulo en el punto de corte de sus diagonales, o en el punto de intersección de las rectas que bisectan sus
lados.
Sea la región plana limitada por la curva
, las rectas
,
y el eje
.
Consideremos una partición del intervalo
Se toma
Consideremos el
.
rectángulo. Este tiene como base
y altura
.
El centro de masa de un rectángulo como ese está localizado en
El momento de un rectángulo con respecto al eje
es
el momento de un rectángulo con respecto al eje
es
y
Por lo tanto
Haciendo el razonamiento usual para cuando la norma de la partición tiende a
límite de cada una de las sumas
,
y para tomar el
cuando
Como siempre es mejor tratar de manejar el concepto que usar las ``fórmulas'' porque así se puede adaptar a
otro tipo de situación por ejemplo para cuando en la región la curva está dada en términos de
intervalo de integración.
así como el
La densidad termina simplificándose al ser uniforme y la expresión de cada denominador termina siendo el área
de la región.
Ejemplo 3: Encontrar el centro de masa de la región limitada por un arco de la función
y el eje
Tomando el arco para
que es una respuesta lógica puesto que la recta
quedar más hacia
que hacia
por la forma de la gráfica
es eje de simetría y que
debe
Ejemplo 4:Encontrar el centro de masa de la región limitada por la curva
que también es una respuesta lógica dado que
y el eje
.
es eje de simetría, que
tiene que
ser negativo y por la forma de la gráfica más hacia 0 que hacia el vértice que queda en
CENTRO DE MASA DE UNA REGIÓN PLANA COMPRENDIDA ENTRE DOS CURVAS.
Basado en el mismo proceso que se hizo para la región plana limitada por una sola curva , usando centro de masa
de un iésimo rectángulo y siendo
Lo cúal conlleva a las integrales
habiendo simplificado
para todo
se deduce
Ejemplo 5: Encontrar el centro de masa de la región limitada por las gráficas de
. Los puntos de intersección de las curvas son
Siendo la recta
y
y
eje de simetría de la región parece razonable la respuesta
Ejemplo 6: Encontrar el centro de masa de la región limitada por la curva
recta
Los puntos de intersección de las dos gráficas se obtienen con
y
los puntos son
y
y la
Los centros de masa obtenidos cuando la densidad es uniforme se llaman centroides
Ejemplo 7: Encontrar el centroide de la región plana de densidad compuesta del triángulo de vértices en los
puntos
y
y por el cuadrado localizado inmediatamente debajo del triángulo
1) Sin integración
Masa del triángulo
Como la región tiene un eje de simetría que es el eje
Las medianas del triángulo( rectas que unen un vértice con el punto medio del lado opuesto ) son ejes de simetría
y éstas se intersectan a
por lo tanto éste estará en
de la distancia del lado correspondiente,en el punto que será el centroide del triángulo;
y como
Para el cuadrado: Masa
Centro de masa en
El momento total es la suma de los momentos:
La masa total es la suma de las masas:
el centroide de la región plana queda entonces en
2) Utilizando integración:
Las ecuaciones de las rectas que conforman los lados del triángulo son
Por simetría
si
y
si
Masa
región)
( se multiplica por dos por simetría de la
el centroide de la región plana queda localizado en