DISTRIBUCIÓN DE VALORES EXTREMOS Tipo I (Tippet Frechet)

11.- ANALISIS DE VIENTOS EXTREMOS
11.1- Distribución De Valores Extremos Tipo I (Tippet Frechet)
Función de distribución acumulada (FDA)
PY ( y )  e  e
Z
(11.1)
e = 2,7182....
Determina la probabilidad que un valor extremo cualquiera Y sea menor que otro
fijado y
PY( y )  Pr ob Y  y 
(11.2)
y = valor que puede tomar Y
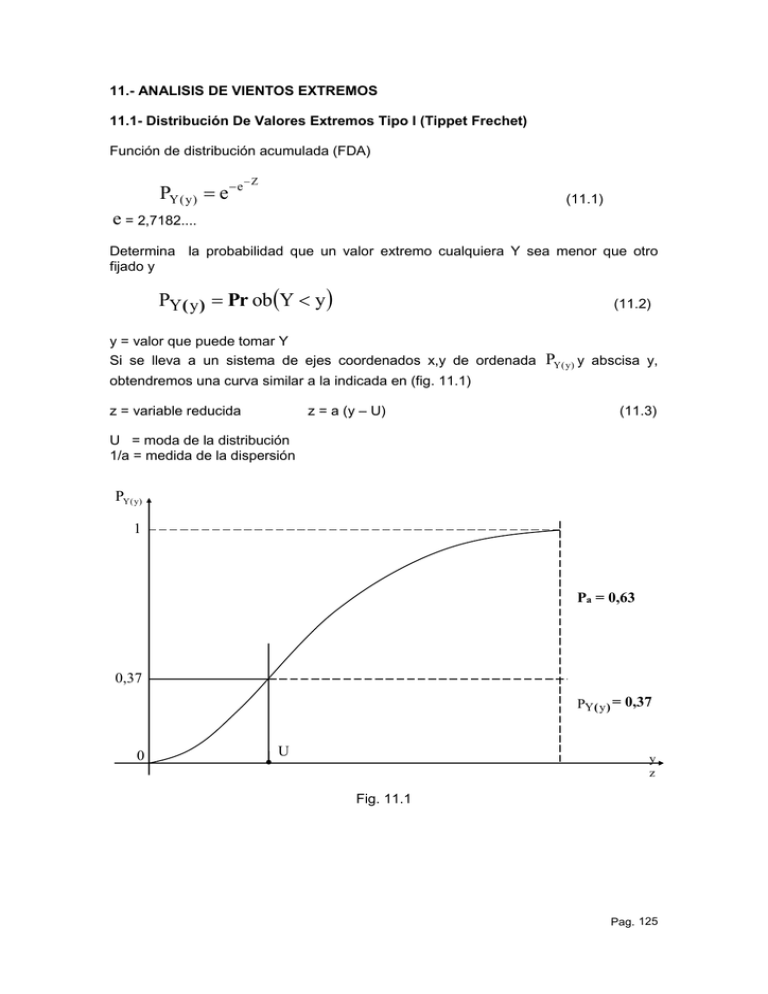
Si se lleva a un sistema de ejes coordenados x,y de ordenada
PY( y) y abscisa y,
obtendremos una curva similar a la indicada en (fig. 11.1)
z = a (y – U)
z = variable reducida
(11.3)
U = moda de la distribución
1/a = medida de la dispersión
PY( y)
1
Pa = 0,63
0,37
PY (y ) = 0,37
0
U
y
z
Fig. 11.1
Pag. 125
PY( y)
37%
0
y
Z=0
y
z
Fig 11.2.
La función de densidad de probabilidades (FDP) correspondiente será (fig 11.2)
p Y( y)  e z  e 
z
(11.4)
La probabilidad que Y sea mayor que y será:
Pa  1  PY( y )  Pr obY  y 
(11.5)
La moda U es la ordenada máxima de la FDP y corresponde a z = 0.
En ese punto
PY( y)  e  e  e 1  0,3679  0,37
z
Pa  1  PY( y)  1  0,3679  0,632  0,63
El área rayada representa el 37% de probabilidad que Y < y, lo cual coincide con el
valor indicado en la ordenada del diagrama FDA.
Pr obY  y  0,37
Pr ob(Y  y)  0,63
El problema consiste en determinar los valores de 1/a y U para poder trazar la curva
FDA.
En este caso, las variables aleatorias serán velocidades extremas anuales sobre un
período de medición de 3 segundos
Y  V̂ ,que es el adoptado por el CIRSOC 102.
Pag. 126
En adelante:
PY ( y )  PVˆ
En una localidad determinada se miden velocidades ,en N años, de igual tamaño T
(período de observación) que puede ser 1 mes o 1 año generalmente. No todos los
valores leídos en el período T se utilizan, sino solamente aquellos que son
estadísticamente independientes En cada año se busca el máximo valor
Se utilizará el ejemplo dado en Cook [1] correspondiente a velocidades medidas en el
aeropuerto de Jersey – USA (1959/78) N = 21 años. Estos valores se colocan en la
Tabla 11.1 en orden creciente del 1 al 21.
Gumbel [2] utiliza un método aproximado basado en el modelo de mínimos cuadrados
para determinar analíticamente U y a. Se minimizan los cuadrados de las desviaciones
de la recta medidas en dirección perpendicular a la recta que se obtendría de los
valores de V y z, volcados en un sistema de coordenadas. (Fig. 11.3)
V̂
Fig. 11.3
z = a ( V̂ - U)
Las ecuaciones halladas son las siguientes:
U  Vˆ
- σ V̂
V̂N
σN
σ
a= N
σ V̂
(11.6)
(11.7)
V̂ = velocidad pico de ráfaga
ˆ = velocidad promedio de las velocidades pico de ráfaga
V
σ V̂ = desviación Standard de la velocidad
σN = desviación Standard esperada
VN = valor medio esperado
En la Tabla 11.2 figuran los valores de VN y σN en función del número de
mediciones para N = 20,  N = 1,06 y VN = 0,52.
Pag. 127
TABLA 11.1
V̂  Vˆ  V̂  Vˆ 
2
N
V̂
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
28.5 -6.67
44.49
29
-6.17
38.07
30
-5.11
26.73
31
-4.12
19.97
31.5 -3.67
13.47
31.5 -3.67
13.47
32.5 -2.17
7.13
34
-1.17
1.37
34
-1.17
1.37
35.5 -0.33
0.23
36
0.83
0.11
36.5 1.33
1.77
37
1.83
3.35
38
2.83
8
38
2.83
8
38.5 3.33
11.09
38.5 3.33
11.09
39
3.83
14.67
39
3.83
14.67
40
4.83
23.33
40.5 5.33
28.41
 = 738,50  = 290,79
V̂  U
z  a V̂  U
-4.8
-4.3
-3.3
-2.3
-1.8
-1.8
-0.8
0.7
0.7
2.2
2.7
3.2
3.7
4.7
4.7
5.2
5.2
5.7
5.7
6.7
7.2
-1.344
-1.204
-0.924
-0.644
-0.504
-0.504
-0.224
0.196
0.196
0.616
0.756
0.896
1.036
1.316
1.316
1.456
1.456
1.596
1.596
1.876
2.016
738,50
m
Vˆ 
 35,17
21
seg
 Vˆ 
1,06
m
 0,28
3,81
seg
U  35,17 
a


PVˆ
p Vˆ
0.022
0.036
0.080
0.149
0.191
0.091
0.286
0.439
0.439
0.525
0.625
0.665
0.70
0.764
0.764
0.792
0.792
0.818
0.818
0.858
0.875
0.001
0.012
0.020
0.087
0.10
0.085
0.056
0.045
0.039
290,79
 3,81
20
3,81.0,52
m
 33,30
1,06
seg
Tabla 11.2
N
VN
N
15
20
30
40
50
60
70
80
90
100
150
200
500

0,51
0,52
0,54
0,54
0,55
0,55
0,55
0,56
0,56
0,56
0,56
0,57
0,57
0,57
1,02
1,06
1,11
1,14
1,16
1,17
1,19
1,19
1,20
1,21
1,23
1,24
1,26
1,28
Pag. 128
Media esperada VN y desviación standard  N (i)
En fig. 11.4 se presenta el diagrama de la función de densidad de probabilidades
(FDP) para lo cual se aplica la (11.4)
Pyy   e z  e
z

Para simplificar, solamente se utilizan algunas velocidades que sean suficientes para
trazar la curva que posee la cola extendida hacia la derecha.
El eje z coincide con el valor de la moda U = 33.3 m/seg.
Si se desea, por ejemplo, alcanzar la velocidad de 39 m/seg. Se debe calcular el área
de la superficie rayada, que es la integral del FDA.
PVˆ 
3

0
p Vˆ dv 
1,596
 p Vˆ dv  0,81
(11.8)
0
Pag. 129
Pag. 130
Pag. 131
La ordenada del diagrama FDA (Fig. 11.5) indica la probabilidad que la velocidad
extrema anual V̂ sea inferior a un valor v
PV̂ = prob (V̂ < v )

(11.9)

Pa  1  PV̂ indica la probabilidad que esa velocidad v sea superada.
Se define como “intervalo medio de recurrencia” R medida en años ,la relación
R = 1/ Pa
De donde
R = 1/Pa
El CIRSOC adopta R = 50 años, con lo cual Pa = 1/50 = = 0,02
Existe una probabilidad del 2 % que la velocidad v sea superada un a vez en un año
cualquiera de los R
Se denomina “período de retorno” S = R. T
Generalmente se considera T = 1 año, por lo cual S = R y se puede,en adelante,
llamar a R= “período de retorno”

 
Pa  prob V̂  v  1  PV̂
PV̂  1  Pa 

(11.10)
(11.11)
Si se consideran otros n años (período de exposición) durante la vida de la
construcción, la probabilidad que la velocidad v no sea superada por lo menos una vez
en n años será:
(PV̂ )n = prob(V < v)n = (1
Pa )n
(11.12)
La probabilidad de ser superada:
1  P    1  1  P 
n
V̂
a
n
(11.13)
En la Tabla 11.2, el máximo valor registrado es V = 40,5 m/seg que corresponde a una
probabilidad 0,875 de no ser superada y 1-0,875 = 0,125 (12,5 %) de ser superada en
un año cualquiera en el período de retorno R = 1/ 125 = 8 años
La probabilidad que la velocidad V sea igualada o superada por lo menos una vez en
un período de exposición n = 20 años será:
Pa  1  1  0,125 20  0,93  93%
(11.14)
El Reglamento CIRSOC 102 establece velocidades pico de ráfaga de 3 segundos
asociadas con una probabilidad anual del 2% de ser superada en un período de
retorno R = 50 años en un período de exposición n = 50 años.
Pa  1/ R  1 50  0,02 
(11.15)
Pag. 132
Pn  1  1  0,0250  0,6358 0,64
(11.16)
Existe una probabilidad Pn del 64% que la velocidad del viento (asociada con una
cierta probabilidad anual Pa = 2%), sea excedida o igualada por lo menos una vez
durante un período de n años.
Si se desea determinar analíticamente que velocidad de la Tabla 11.2 corresponde a
Pa = 0,02.
PV̂  1  Pa  e  e
De (11.8)
z
(11.17)
Si se aplican logaritmos:
ln(1 Pa ) = e z
- ln(1 Pa ) = e z
ln( ln(1 Pa )) = z
z = ln[ ln(1 Pa )] = a(V̂ U)
(11.18)
aV̂ = aU ln[ ln(1 Pa )]
1
ln[ ln(1 Pa )]
a
V̂ = U
V̂ = 33,3
(11.19)
1
ln[ ln(1 0,02)] = 47,23
0,28
Si se busca en el diagrama FDA, se obtiene un valor parecido.
De (11.18):
z = ln[ ln(1 Pa )]
1 Pa = PV̂
z = ln ln PV̂
(
)
PV̂ = 0,98
z = ln( ln 0,98) = 3,9
Se puede generar un gráfico que linealiza la curva FDA colocando en abscisa
ln lnPV̂ y en ordenada las velocidades V̂ (Fig. 11.6).
(
)
Una vez ubicados los puntos correspondientes se traza la recta de ajuste en base a
mínimos cuadrados.
Pag. 133
V̂
50
47,23
45
1
y zU
a
40
0,33
35
33,5
30
Fig. 11.6
25
20
15
10
5
0
-1
0
1
2
3
3,9 4

z   ln  ln PV̂

Para z = 3,9 corresponde V̂  47m / seg
Donde z= 0 V = 33 m/seg (moda)
La tangente a la recta mide
1
a
En el gráfico hallamos 1/a = 0,30
La expresión de la tangente será:
1
1
z  U  3,9  33,3  47,23
a
a
1 47,23  33,3

 3,57
a
3,9
1
a
 0,28
valor similar al hallado anteriormente
3,57
y
11.2.- Estimacion De Probabilidades (Metodo de Gumbel)
En realidad los valores experimentales no siguen exactamente la distribución teórica y
se puede buscar una forma de determinar las probabilidades, basada únicamente en
la ubicación de la variable.
Dice Cook [7]:
“Los extremos son ranqueados hacia ascendente orden de magnitud. La posición de
cada extremo en esta secuencia lograda se define como rango m. El menor tiene el
rango m = 1, el segundo tiene el rango m = 2 y el más alto m = N, si hay N valores
Pag. 134
extremos en los datos. Es conveniente usar el símbolo υ̂(m) para denotar el valor del
extremo de rango m en la ecuación (entonces υ̂(m) es V̂2 o V 2 en los ejemplos)
Usando el conocimiento de N observaciones pasadas es posible sacar conclusiones
sobre el probable valor de cada siguiente observación, la N+1 observación.
Si es menor que el primer extremo ranqueado υˆ (m = 1) habrá solamente un valor
afuea de N+1 extremos.
La estimación de esta ocurrencia es:
1
Pυ(m 1) =
N +1
(11.20)
.
Similarmente, si es mayor que el último ranqueado υˆ (m = N) , luego N fuera de N+1 es
menor y el estimativo de este rango es
Pυˆ (m =1) =
N
N +1
En el caso general de υ̂(m) el estimado es Pυˆ (m =1) =
(11.21)
m
N +1
(11. 22)
La palabra “estimado” se usó deliberadamente para indicar que los valores resultantes
de Pυ̂ no son exactos por las siguientes razones:



1
El valor Pυˆ (m) sólo puede ser discriminado para incremento de
.
N +1
El correspondiente valor de υ̂ solamente puede ser discriminado para
incremento que dependen del anemómetro utilizado
El registro puede no ser representativo de la distribución total.
“Nótese que el rango de los extremos es el mismo si υ̂ es V o V2, luego la estimación
de P es la misma en ambos modelos.
El método de Gumbel se aplica usualmente a un grupo de velocidades máximas
anuales, esto es que cada valor es la máxima velocidad del viento que produce en un
período de 1 año.
Pag. 135
TABLA 11.3
Maximum gust wind speeds for Jersey:
Intermediate data for Gumbel plot
Gust
Reduced
Rank CDF
speed2
variate
PV̂ 2
m
2
2
z
V̂ (m/s)
812
1
0.045 -1.129
841
2
0.091 -0.875
961
3
0.136 -0.689
961
4
0.182 -0.533
992
5
0.227 -0.393
992
1056
1156
1156
1260
6
7
8
9
10
0.273
0.318
0.364
0.409
0.455
-0.262
-0.136
-0.012
0.122
0.238
1296
1332
1369
1444
1444
11
12
13
14
15
0.500
0.545
0.591
0.636
0.682
0.366
0.501
0.642
0.784
0.960
1482
1482
1521
1521
1600
1640
16
17
18
19
20
21
0.727
0.772
0.818
0.864
0.909
0.955
1.144
1.355
1.606
1.920
2.351
3.068
Se reproduce la Tabla C2 de Cook [7] donde las velocidades están al cuadrado y la
probabilidad es la correspondiente a V2 (Tabla 11.3 ).
En la Fig. C1 de Cook [1] se colocan en ordenadas las velocidades al cuadrado y en
abscisas la variable reducida z = ln ln PV 2 .(Fig. 11.7)
Así se obtiene gráficamente la recta representativa de la variación.
(
)
Pag. 136
Re duced variate,z   ln ln P   lnnm / lN  l
Fig. 11.7 [Ref. 7]
Para z = 0, se obtiene el valor de UV 2 y la pendiente de la recta determina el valor de
1 aυ2 .
1 a υ 2 = 245(m / s)2
UV 2 = 1120(m / s)2
Para hallar la velocidad correspondiente a un período R partimos de la (11.19)
V̂ = U 1 a [ ln( ln(1 Pa ))] = U + 1 a [ ln( ln(1 1 R))]
Esta expresión es similar a:
V̂ = U ( ln R)
Cook trabaja con velocidades al cuadrado.
V̂ 2 = UV 2
V̂ = Uυ 2
1
aU2
1
aU2
( ln R)
R = 50 años
0,5
( ln R)
= [1120 245( ln 50)]0,5 = 45,6 m s
46 m s
z = ln( ln 0,98) = 3,90
En la Fig. 11.7 se obtiene valores similares
V 2 = 2116
11.3.- Aplicaciones Al Reglamento Cirsoc 102
El Reglamento CIRSOC 102 (94) [0] que se denominará en adelante C-94 fue
reemplazado por el Reglamento CIRSOC 102 (01), en adelante C-01 [1].
El mapa de la República que presenta el C-94 contiene curvas de nivel de velocidades
instantáneas máximas anuales obtenidas utilizando una distribución de extremos Tipo
Pag. 137
II, sin considerar el período de exposición n, que luego es tenido en cuenta mediante
un coeficiente de velocidad probable Cp. La mayoría de los Reglamentos (ASCE,
British Standard, NB, etc.) utilizan la distribución Tipo I y los mapas ya están
incluyendo el tiempo de exposición n. Cuando se cambió el Reglamento, CIRSOC
decidió aplicar este último criterio para lo cual era necesario modificar el mapa.
Raimundin y Cudmani [27], aconsejaron determinar un nuevo valor de Cp en base a la
distribución Tipo I y ya con el tiempo de exposición incluido.
C-94
V0 = velocidad básica de diseño
C-01
V: velocidad básica de viento
velocidad de ráfaga de 3 seg. para
V0  .Cp
Categoría de exposición C.
Cp : coeficiente de velocidad probable en Pa = 0,02 n = 50 años
función de n y
:
Pn
Pn = 0,64
velocidad promedio de velocidades
instantáneas pico de ráfaga sobre 3 seg.
para Pa = 0,02
Pm
de 0,01 a 0,50
m de 2 a 100 años
Valores Extremos Tipo II
PVˆ
ˆ 
V

  

e  
Valores Extremos Tipo I

 = 7,14
PVˆ  e
 e  a V  U 
ˆ
(11.26)
(11.23)
Valor Medio:
ˆ  1  1 
V
 


(11.24)
ˆ  U  0,577276
V
a
(11.27)
(11.25)
 Vˆ 

6a
(11.28)
Desviación Standard:
  2
 1 
 V̂  1    1  
  
  
 : Función gamma de Gauss

Fx    e  t .e x 1dt
0
Si se igualan (11.24) con (11.27) y (11.25) con(11.28)
Pag. 138
 
1 
0,577216
1  7,14    
a

 

 3,14  1  2    2 1  1 


 2,4494 .a
 7,14 
  7,14 

(11.29)
(11.30)
Desarrollando la (11.29)
0,57726
a
0,157726
1,103  U 
a
 0,8599  U 
(11.31)
Desarrollando la (11.30)

1,2885
  0,7199   2 0,8599
a
1,2885
 0,05139
a
25,0730
a


(11.32)
Reemplazando la (11.32) en la (11.31)
0,577276
25,073
U  1,0799   
1,103  U 
Raimundin obtiene un valor menor:
U  1,001898 
Se puede aceptar que la moda de la del Tipo I es igual a la velocidad de referencia de
la del Tipo II.
Viollaz y Salvatierra [26], revisaron los valores de velocidades de las 19 ciudades
incluídas en el C-94 y agregaron otros con la contribución de la Dra. Schwartzkopf,
dibujando un mapa con mayor densidad de isopletas y colocando los nuevos valores
adecuados a la distribución Tipo I.
Si se aplican logaritmos a la (11.1)

z   ln  ln PVˆ

(11.33)
Pag. 139
De (11.11):
 
Pn  1  PVˆ n
 
} aV 
a V  U   ln ln{1 P }
De donde:
z   ln - ln{1 Pn
1
n
n
U
(11.34)
1
n
Despejando V
1 
1

V  U 1 
ln1  Pn  n 
 Ua

(11.35)
1 
 1
Cp  1 ln1  Pn  n 
 Ua

V  .Cp
(11.36)
Para el aeropuerto de Córdoba se encontró
U    27 m
seg
1  3,8 m
a
seg
Reemplazando en la (11.26)
 3,8

Cp  1 
ln ln1  0,64 
 27

Cp  1,55
V  27.1,55  41,85  42
m
seg
que es el valor hallado por Viollaz.
En el C-01 figura para la ciudad de Córdoba
41
m
seg
En el C-01 se utiliza la nomenclatura “intervalo medio de recurrencia “R que es similar
a “período de recurrencia” Figura la Tabla A-1(Tabla 11.4) en el Apartado A en función
del riesgo de la construcción.
Categoría
I
I
II
III
IV
0,87
1
1,15
1,15
Pa
0,04
0,02
0,01
0,01
Tabla 11.4
N
25
50
100
100
Si la construcción es de bajo riesgo (Categoría I), se puede reducir el intervalo de
recurrencia a R = 25 años ,por lo cual las presiones pueden modificarse a través de
I = 0,87, donde Pa = 1/25 = 0,04 con lo cual ya hay una probabilidad mayor de ser
excedida la velocidad en cualquier año en 25 años.
Pag. 140
Si la construcción es de alto riesgo ,debe tenerse en cuenta un intervalo de recurrencia
mayor, que es de 100 años. En ese caso, Pa= 1/100 = 0.01 con lo cual el riesgo sería
del 1 % e I = 1,15.
En los Comentarios del CIRSOC 102 figura la Tabla C2 donde figuran diversos valores
de período de exposición n en relación a la probabilidad anual Pa (Tabla 11.5) y se
obtienen los valores de la probabilidad de ocurrencia Pn .
Tabla 11.5
Probabilidad
anual, Pa
Período de referencia (exposición), n (años)
1
5
10
25
50
100
0,04 (1/25)
0,02 (1/50)
0,01 (1/100)
0,005 (1/200)
0,04
0,02
0,01
0,005
0,18
0,10
0,05
0,02
0,34
0,18
0,10
0,05
0,64
0,40
0,22
0,10
0,87
0,64
0,40
0,22
0,98
0,87
0,64
0,39
Si usáramos otra probabilidad, por ejemplo para Pa = 0,02 = 1/125 (intervalo de
recurrencia 25 años)
Pn = 1 – (1-0,02)25 = 0,40
Probabilidad del 40% que esa velocidad sea igualada o excedida una vez a lo largo de
un período de exposición n = 25 años.
Si se usan valores de Pa distintos a 0,02 , deben afectarse los valores de los
coeficientes I de la Tabla 11.4 mediante el factor de conversión establecido en la Tabla
C3 de los Comentarios (Tabla 11.6)
Tabla 11.6
Velocidad de pico de ráfaga para un intervalo
medio de recurrencia de N = 50 años
Intervalo medio de
Factor de
Pa
recurrencia (R
conversión
años)
500
1,23
0,002
200
1,14
0,005
100
1,07
0,010
50
1,00
0,02
25
0,93
0,04
10
0,84
0,10
5
0,78
0,20
Pag. 141