UNIDAD 3 COEFICIENTE GLOBAL DE TRANSFERENCIA DE CALOR
Anuncio
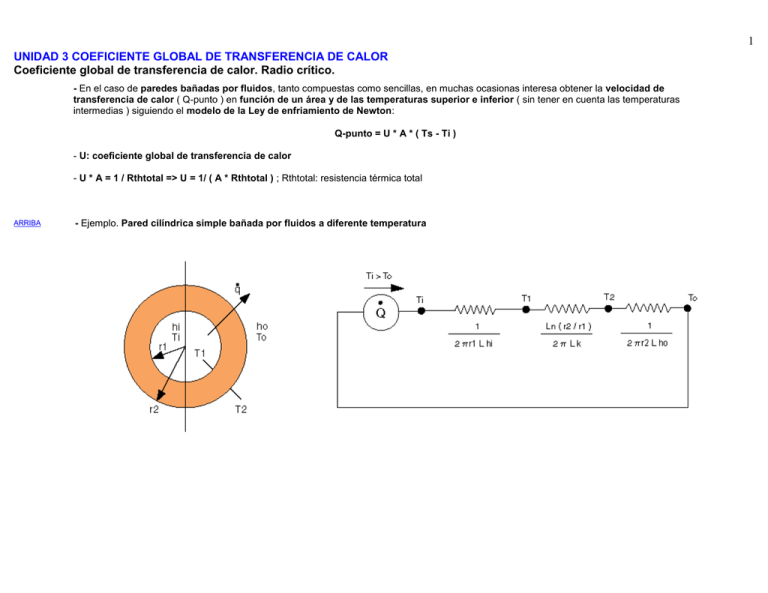
1 UNIDAD 3 COEFICIENTE GLOBAL DE TRANSFERENCIA DE CALOR Coeficiente global de transferencia de calor. Radio crítico. - En el caso de paredes bañadas por fluidos, tanto compuestas como sencillas, en muchas ocasionas interesa obtener la velocidad de transferencia de calor ( Q-punto ) en función de un área y de las temperaturas superior e inferior ( sin tener en cuenta las temperaturas intermedias ) siguiendo el modelo de la Ley de enfriamiento de Newton: Q-punto = U * A * ( Ts - Ti ) - U: coeficiente global de transferencia de calor - U * A = 1 / Rthtotal => U = 1/ ( A * Rthtotal ) ; Rthtotal: resistencia térmica total ARRIBA - Ejemplo. Pared cilíndrica simple bañada por fluidos a diferente temperatura 2 -- Según la analogía termoeléctrica Q-punto = ( Ti - To ) / Rthtotal ; Q-punto = U * A * ( Ti - To ) => U * A = 1 / Rthtotal => 1 / ( U * A ) = Rthtotal ARRIBA - El coeficiente global de transferencia, U, depende de la superficie que se considere, interior ( A1 ) o exterior ( A2 ) . - Si A = A1 = 2 pr1 L => - Si A = A2 = 2 pr2 L => 3 ARRIBA RADIO CRÍTICO. RELACIÓN CRÍTICA DE AISLAMIENTO - Al incrementar el grosor del aislamiento térmico de una pared plana siempre disminuye la transferencia de calor. Cuanto más grueso sea el aislante más baja será la velocidad de transferencia de calor. Esto es así debido a que el área de la superficie de intercambio de calor paredfluido no varía. - No ocurre lo mismo con las paredes cilíndricas o esféricas. En este caso, la resistencia total, y por tanto la potencia térmica, varía con el valor del radio exterior del aislamiento. Dicha variación responde a la curva de la figura: - Esto es debido a que el aislamiento adicional incrementa la resistencia a la conducción pero al mismo tiempo disminuye la resistencia a la convección debido al aumento del área exterior. 4 ARRIBA - Para calcular el radio crítico se parte de la expresión de transferencia de calor correspondiente al tipo de pared considerado ( ver pared cilíndrica y pared esférica en el capítulo II ) en función de r2 , Q-punto ( r2 ) , se deriva esta expresión respecto a r2 , se iguala a 0 y se despeja r2. El valor resultante de r2 será el correspondiente al radio crítico. - Aproximadamente, si r1 < r2 < [ radio crítico + ( radio crítico - r1 ) ] la velocidad de transferencia de calor aumenta respecto a la pared sin aislamiento, si r2 > [ radio crítico + ( radio crítico - r1 ) ] la velocidad de transferencia de calor disminuye respecto a la pared sin aislamiento. - Expresiones del radio crítico -- PARED CILÍNDRICA => RADIO CRÍTICO = ka / ho ; ka: conductividad del aislante ; ho: coeficiente de película -- PARED ESFÉRICA => RADIO CRÍTICO = ( 2 ka ) / ho ; ka: conductividad del aislante ; ho: coeficiente de película - CUESTIONES PRÁCTICAS. - 1 ) En la mayoría de los casos no es necesario considerar el radio crítico como condición de diseño. Para valores coherentes de ka y ho se obtienen valores para el radio crítico del orden de 1 cm. Cualquier tubería, conducto o depósito supera con creces ese valor. ARRIBA - 2 ) Podría haber problemas en el caso del aislamiento de los conductores eléctricos cuyo radio es mucho menor de 1 cm, pero en este caso lo que se pretende es un aislamiento eléctrico y no térmico, puesto que interesa que el calor se disipe lo más rápido posible para evitar sobrecalentamientos. Por lo tanto el radio critico tampoco es un factor determinante en este caso.





