Evidencia 5 MIC

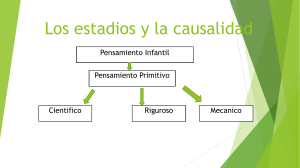
UNIDAD 1
LA CIENCIA COMO UNA CONSTRUCCIÓN HISTÓRICO-SOCIAL
Elemento de Competencia: II. Modelo Aristotélico
EVIDENCIA No. 5
Tema: La evolución de la ciencia y de sus explicaciones
a.- ¿Cuáles son las dos direcciones, a lo largo de la historia de la ciencia, en
que el concepto de explicación científica ha sido examinado
filosóficamente?
R= 1) desde el punto de vista de una teoría de la argumentación
2) como parte de la búsqueda de criterios filosóficos que nos permitan distinguir
las creencias que constituyen un conocimiento objetivo el mundo (ciencia), de las
que sólo reflejan la ilusoria realidad (conceptos de uso cotidiano).
b. ¿Por qué está constituida la ciencia?
R= por tradiciones de razonamiento y en particular, por patrones o modelos de
explicación que se constituyen y se desarrollan históricamente a lo largo de siglos.
c. ¿Cómo deben verse los diferentes patrones o modelos de explicación
científica?
R= como horizontes conceptuales en los cuales se articula de la manera más
general posible la forma en que se entiende la relación entre el mundo y nuestras
capacidades cognoscitivas para entender cómo es el mundo.
d. ¿Por qué el conocimiento es un proceso histórico?
R=porque la explicación científica no puede responderse satisfactoriamente en
abstracto, es necesario entender los diferentes contextos históricos en los cuales
la pregunta ha sido planteada, así como los problemas y las tradiciones de
pensamiento que han contribuido a su examen.
e. ¿Qué es un patrón o modelo de explicación científica?
R= consiste en una determinada manera de explicar algo científicamente.
f. ¿Cuáles aspectos incorpora o forman parte de un patrón de explicación
científica?
R= las nociones interconectadas de causalidad y ley de la naturaleza, adopta una
manera de concebir la relación del todo con las partes y acepta ciertas reglas
acerca del alcance y del tipo de inferencias que podemos hacer a partir de la
experiencia.
g. ¿Por qué, a pesar de que no podemos hablar en sentido estricto de una
metodología científica en los albores de la ciencia, no puede haber ciencia
sin método?
R= porque el primer pensamiento científico va acompañado, implícitamente, de su
método, al abordar los objetos que las necesidades prácticas concretas le
imponen.
h. ¿Dónde se da la ciencia y cuál es su primer método?
R= Donde el hombre comienza a operar (consciente o inconscientemente) con la
idea elaborada de la causalidad, en lo concreto de la práctica.
UNIDAD 1: LA CIENCIA COMO UNA CONSTRUCCIÓN HISTÓRICO-SOCIAL
Elemento de Competencia: II. Modelo Aristotélico
Elaborado por: MLE. Alma Mireya Flores Juárez
i. ¿Dónde comienza la metodización?
R= donde a través de la observación se llega en la práctica a la concepción de
que, dados ciertos fenómenos o circunstancias, se producen en sucesión temporal
otros que aparecen como condicionados por los que les anteceden.
j. ¿En qué consiste la causalidad?
R= en descubrir que unos fenómenos son causa y otros efecto. Es decir, que todo
efecto o fenómeno tiene una causa que le antecede.
k. ¿Cómo se va a dar el progreso del pensamiento científico a partir de la
causalidad?
R= en la medida en que el hombre depure los fenómenos antecedentes,
concomitantes y consecuentes y escoja uno o algunos de ellos sin los cuales no
se producirían los efectos observados.
l. ¿Por qué el trayecto de las ciencias empíricas fue más largo que el de la
geometría y aritmética?
R= porque tratan de encontrar un cuerpo teórico debido a la necesidad de
acumular datos, hechos y experiencias que sirvan de contenido para la
abstracción generalizadora y derivadora de leyes que establezcan las relaciones
causales que permiten hacer predicciones exactas.
m. El desarrollo de la ciencia empírica primitiva tiene otro método que
ayudará a desbrozar sus terrenos conceptuales, ¿cuál es éste, cómo se
transmite y cómo funciona?
R= Es el método de ensayos y errores, se transmite por tradición oral en forma de
preceptos plagados de supersticiones y mitos, los cuales eran en definitiva formas
de explicación de los fenómenos naturales y suplían la necesidad humana de dar
respuesta a fenómenos que de otra manera, hubieran permanecido en el campo
del misterio.
n. ¿Qué son las analogías antropomorfizantes?
R= Se refieren a que las propiedades y cualidades humanas son atribuidas a las
cosas y también las de la naturaleza orgánica a la inorgánica y viceversa.
ñ. ¿Cuál es el método comparativo?
R= en este estadio de desarrollo, en su búsqueda de semejanzas y diferencias
entre las cosas, hace posible una confusión en la cual el hombre, aún no
totalmente diferenciado de la naturaleza, no se concibe a sí mismo como algo
distinto.
UNIDAD 1: LA CIENCIA COMO UNA CONSTRUCCIÓN HISTÓRICO-SOCIAL
Elemento de Competencia: II. Modelo Aristotélico
o. ¿Por qué el método comparativo, en este estado inicial de la ciencia,
provoca confusiones?
R= porque el hombre, inmerso en la naturaleza, no distingue entre sus creaciones
y las de la naturaleza; entre lo explicado y la explicación, el nombre y la cosa
mencionada, entre el orden universal y el orden social.
p. ¿Por qué en la cultura griega se superará este primer estado de la
ciencia?
R= porque se intentará explicar la naturaleza por sí misma.
q. ¿Qué factor jugará un papel fundamental en la superación de este primer
estado de la ciencia?
R= el lenguaje
r. ¿Qué hará posible el desarrollo de la lógica?
R= el perfeccionamiento del lenguaje
s. ¿Dónde se forman las primeras ideas fundamentales de la metodología del
conocimiento científico?
R= comenzaron a formarse en la antigüedad, en la vieja Grecia.
t. ¿Cuáles métodos científicos representan el gran aporte de los griegos a la
metodología científica?
R= 1) El método axiomático y su brillante aplicación a la elaboración de los
principios geométricos de Euclides. 2) El método hipotético-deductivo y su
fructífera utilización en las investigaciones de Arquímedes sobre estática.
u. ¿Qué problema ocasionó el que la antigüedad griega desconociera, en
general, las ciencias empíricas?
R= el que los filósofos griegos se ocuparan casi exclusivamente de los problemas
metodológicos de las ciencias deductivas y en particular de las matemáticas.