c bx a x

FUNCIÓN RAÍZ CUADRADA
La ecuación que representa a la función raíz cuadrada corresponde a:
f ( x)  a  bx  c
El dominio de la función corresponde a los valores obtenidos al desarrollar la desigualdad a + bx 
0. Una vez obtenido el dominio, se elabora una tabla de valores, se grafica y se obtiene el
recorrido.
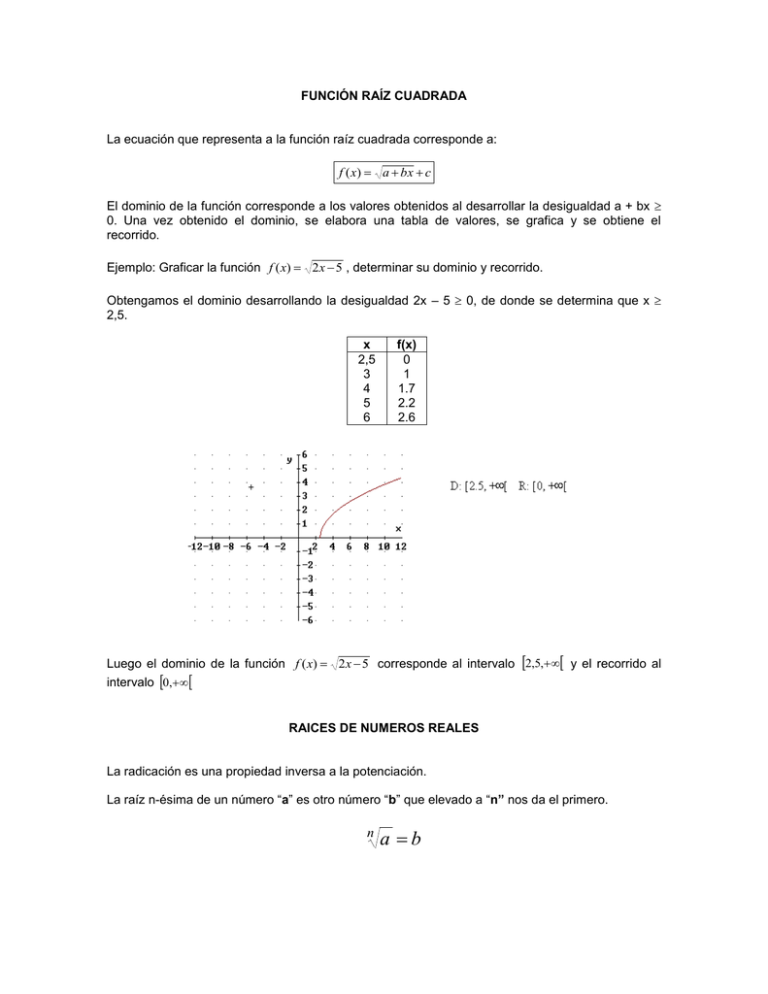
Ejemplo: Graficar la función f ( x)  2x  5 , determinar su dominio y recorrido.
Obtengamos el dominio desarrollando la desigualdad 2x – 5  0, de donde se determina que x 
2,5.
x
2,5
3
4
5
6
f(x)
0
1
1.7
2.2
2.6
Luego el dominio de la función f ( x)  2x  5 corresponde al intervalo 2,5, y el recorrido al
intervalo 0,
RAICES DE NUMEROS REALES
La radicación es una propiedad inversa a la potenciación.
La raíz n-ésima de un número “a” es otro número “b” que elevado a “n” nos da el primero.
n
a b
PROPIEDADES DE LAS RAÍCES
1. Suma y resta de raíces:
Solo se pueden sumar y restar raíces semejantes, o sea del mismo índice y mismo radicando:
7 7 2 7
Como se puede comprobar, la raíz de una suma o resta no es la suma de raíces:
16  9  16  9
2. Producto y división de raíces:
Solo se pueden multiplicar y dividir raíces del mismo índice:
3
3
8 • 3 27  8  27  3 216  6
64 : 4  64 : 4  16  4
De manera inversa de puede enunciar que la raíz de un producto es el producto de raíces (lo
mismo para el cociente):
16 • 4  16 • 4  4  2  8
27  9  3  9  3  3 3 (Descomponer una ra{iz)
16

25
16
25

4
5
3. Raíz de una raíz:
Para calcular la raíz de una raíz, se multiplican los índices.
3
a 6 a
4. RACIONALIZAR:
“Consiste en eliminar las raíces del denominador.”
Casos:
1º Que el denominador sea una raíz cuadrada: en este caso se multiplica numerador y
denominador por la misma raíz.
5
5
2 5 2



2
2
2
2
2º Que el denominador no sea una raíz cuadrada: en este caso se multiplica numerador y
denominador por una raíz del mismo índice que el denominador, pero con un radicando elevado a
un exponente que pueda eliminar raíz del denominador.
5
3
2
53 2 2

3
2 • 3 22

53 4
2
3º Que el denominador sea un binomio con raíces cuadradas: en este caso debemos de multiplicar
numerador y denominador por el conjugado.
2
5 3

2 • (5  3 )
(5  3 ) • (5  3 )

10  2 3
5 
2
 3
2

10  2 3 10  2 3

25  3
22
ECUACIONES IRRACIONALES
Son aquellas en las cuales la incógnita está en la cantidad subradical.
Para resolver una ecuación irracional se despeja la raíz que contiene la incógnita, luego se elevan
ambos miembros al índice de la raíz para eliminar esta y finalmente se calcula la incógnita como
una ecuación lineal cualquiera.
Ejemplo:
3 15  x  5  17
3 15  x  12
15  x  4
( )2
15 – x = 16
-x = 1
x = -1
EJERCICIOS
1. El valor equivalente a
a) 0,25
b)
0,5 es:
2
c)
2
2
d)
e) 1
1
2
2. El Dominio de la función f ( x)  2  3x es
a) x 
2
3
b) x 
3
2
3. La expresión equivalente a
a) 2 6
c) x 
2
3
d) x 
3
2
e) 2 - 3x = 0
12 es
b) 2 3
c) 3 2
d) 6 2
e) 6
d) 4 cm.
e) 64
4. Determinar el lado de un cuadrado de área 8 cm 2
a) 2 cm.
b) 2 2 cm.
c) 4 2 cm.
5. Determinar el volumen de un cubo cuya área total es 12 cm 2.
a) 2 cm3
b) 8 cm3
c)
2 cm3
d) 2 2 cm3
e) 123 cm3
6. ¿Cuál de los siguientes tríos corresponde a un trío pitagórico?
a) 1, 2, 3
b) 1, 3, 5
c) 11, 12, 13
d) 1,
2,3
e) 3, 4, 5
7. Determinar el lado de un cuadrado inscrito en una circunferencia de radio 2 cm.
a) 2 cm.
b) 4 cm.
8. El valor de x en la ecuación
a) –1/2
10
1
 2
d) 2 2
e) Ninguna de
las anteriores
c) 1/2
d) 1/4
e) No tiene
solución
2 ( 3  2 ) se obtiene:
b) 2 6
10. Al racionalizar la expresión
a)
2
x 2  2 x  x  1 es
b) –1/4
9. Al resolver la expresión
a)
c)
b) – 2
c)
2
2 2
6 2
d)
5 2
d)
2 2
3
e)
7
se obtiene:
c) 2  2
e) Ninguna de
las anteriores
ALTERNATIVAS
1.
Alternativa A. Incorrecta. Se confunde extraer raíz cuadrada con obtener la mitad del número.
Alternativa B. Incorrecta. Se transforma 0,5 en 1/2, pero luego se invierte la fracción 1/2, en un
error algebraico que lleva a esta alternativa.
Alternativa C. CORRECTA. Lo primero es transformar el decimal 0,5 en fracción, o sea, en 1/2
para luego racionalizar y obtener esta alternativa.
Alternativa D. Incorrecta. Se transforma 0,5 en 1/2, pero al escribirlo con la respectiva raíz se
considera afectando sólo al numerador de la fracción.
Alternativa E. Incorrecta. No hay claridad en el concepto de raíz, calculándose el doble de 0,5.
2.
Alternativa A. CORRECTA. Para determinar el dominio hacemos 2 – 3x  0, obteniéndose que
x  2/3.
Alternativa B. Incorrecta. El error se produce al despejar equivocadamente x.
Alternativa C. Incorrecta. Al multiplicar la inecuación por –1, la desigualdad cambia, lo cual no
se aplicó y llevó a esta alternativa.
Alternativa D. Incorrecta. Mal despeje y no se cambia la desigualdad al multiplicar por –1.
Alternativa E. Incorrecta. La expresión 2 – 3x = 0 considera sólo un valor del dominio y no la
totalidad.
3.
Alternativa A. Incorrecta. Se descompone en
2·6 para luego obtener, en forma equivocada,
2 6
Alternativa B. CORRECTA. La
12 equivale a
Alternativa C. Incorrecta. Se descompone
4· 3  2 3
12  3·4 para luego obtener
.
Alternativa D. Incorrecta. Se descompone 12 en 6·2 obteniéndose luego 6 2
Alternativa E. Incorrecta. Se confunde extraer raíz cuadrada con obtener la mitad del número.
4.
Alternativa A. Incorrecta. El error se produce al confundir área con perímetro.
Alternativa B. CORRECTA. Si el lado del cuadrado es x, entonces su área es x2 = 8, de donde x =
2 2
Alternativa C. Incorrecta. Se aplica el teorema de Pitágoras que no tiene relación con el enunciado
del problema.
Alternativa D. Incorrecta. Se determina que el valor de cada lado es 4, al dividir el área en dos
partes iguales.
Alternativa E. Incorrecta. Se considera erróneamente el lado con medida 8, resultando el área de
64 cm2.
5.
Alternativa A. Incorrecta. Corresponde al área de cada cara del cubo.
Alternativa B. Incorrecta. Se determina que la arista del cubo es 2, lo que lleva a que el volumen es
8 cm3.
Alternativa C. Incorrecta. El valor 2 corresponde a la arista del cubo y no a su volumen.
Alternativa D. CORRECTA. Si el cubo es de arista a, entonces su área es 6a2 = 12, de donde a =
2 . El volumen queda determinado al efectuar ( 2 ) 3  8  2 2 .
Alternativa E. Incorrecta. Se comprende mal el enunciado, tomándose 12 como la medida de la
arista del cubo.
6.
Alternativa A. Incorrecta. Al resolver 12  2 2  5 , se verifica que es distinto a 32 = 9, por lo tanto
estas medidas no corresponden a los lados de un triángulo rectángulo.
Alternativa B. Incorrecta. Se verifica que 12  3 2  10 es distinto a 52 = 25, por lo tanto estas
medidas no corresponden a los lados de un triángulo rectángulo.
Alternativa C. Incorrecta. Se verifica que 112  122 es distinto de 132, por lo tanto estas medidas no
corresponden a los lados de un triángulo rectángulo.
2
Alternativa D. Incorrecta. Al resolver 12  2 se obtiene 3 y es distinto a 32 = 9, por lo tanto estas
medidas no corresponden a los lados de un triángulo rectángulo.
Alternativa E. CORRECTA. Si resolvemos 3 2  4 2 resulta 25, que es lo mismo que 52 = 25, por lo
tanto las medidas dadas corresponde a un triángulo rectángulo de catetos 3 y 4, y de hipotenusa 5.
7.
Alternativa A. Incorrecta. Errores algebraicos llevan a obtener 2 cm. para el lado del cuadrado
inscrito.
Alternativa B. Incorrecta. Se confunde cuadrado inscrito con cuadrado circunscrito y eso lleva a
considerar esta alternativa como la correcta.
Alternativa C. Incorrecta. Errores algebraicos de procedimiento llevan a optar por 2
Alternativa D. CORRECTA. Como el radio de la circunferencia es 2, la diagonal del cuadrado es 4.
Luego se aplica el teorema de Pitágoras, obteniéndose que el lado mide 2 2 .
Alternativa E. Incorrecta. Diversos procedimientos llevan a esta alternativa.
8.
Alternativa A. Incorrecta. Al elevar al cuadrado la ecuación se debe tener presente la formación de
un cuadrado de binomio en uno de sus miembros.
Alternativa B. CORRECTA. El primer paso es elevar al cuadrado la ecuación con el fin de eliminar
la raíz cuadrada. De esto resulta que x2 + 2x = x2 – 2x + 1, de donde x = -1/4.
Alternativa C. Incorrecta. Al elevar al cuadrado la ecuación, sin considerar que en uno de sus
miembros se forma un cuadrado de binomio, lleva a este error.
Alternativa D. Incorrecta. Un error algebraico lleva a obtener 1/4 como solución de la ecuación.
Alternativa E. Incorrecta. Se eleva al cuadrado y un error de signo lleva a que se simplifiquen todas
las x, determinándose que la ecuación no tiene solución
9.
Alternativa A. Incorrecta. Se suma
6  4 equivocadamente.
Alternativa B. Incorrecta. Al obtenerse
6  2 se suman estas expresiones, llegando al error 2 6 .
Alternativa C. CORRECTA. Se efectúa el producto, obteniéndose
6  4  6 2.
Alternativa D. Incorrecta. Al multiplicar 2 por 3 se obtiene 5 , lo que está incorrecto.
Alternativa E. Incorrecta. Doble error al sumar raíces no semejantes y luego sumar en vez de
multiplicar las raíces.
10.
Alternativa A. Incorrecta. El error se produce al simplificar por 2.
Alternativa B. Incorrecta. Se simplifica por 2 y no se considera el 1 del numerador.
Alternativa C. CORRECTA. Se racionaliza por el conjugado, es decir, por 2  2 con lo que se
obtiene
42 2
 2 2
2
2 2
3
Alternativa E. Incorrecta. Diversos errores de procedimiento o algebraicos llevan a esta alternativa.
Alternativa D. Incorrecta. Se racionaliza erradamente por 2  2 y se obtiene