Presion de vapor

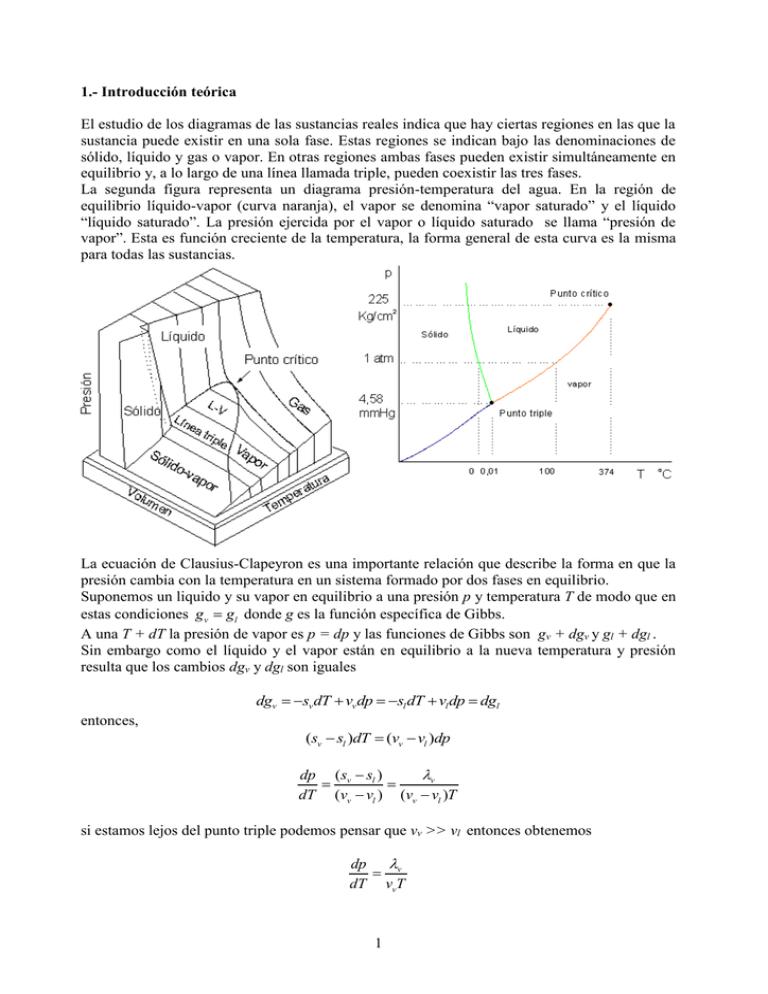
1.- Introducción teórica
El estudio de los diagramas de las sustancias reales indica que hay ciertas regiones en las que la
sustancia puede existir en una sola fase. Estas regiones se indican bajo las denominaciones de
sólido, líquido y gas o vapor. En otras regiones ambas fases pueden existir simultáneamente en
equilibrio y, a lo largo de una línea llamada triple, pueden coexistir las tres fases.
La segunda figura representa un diagrama presión-temperatura del agua. En la región de
equilibrio líquido-vapor (curva naranja), el vapor se denomina “vapor saturado” y el líquido
“líquido saturado”. La presión ejercida por el vapor o líquido saturado se llama “presión de
vapor”. Esta es función creciente de la temperatura, la forma general de esta curva es la misma
para todas las sustancias.
La ecuación de Clausius-Clapeyron es una importante relación que describe la forma en que la
presión cambia con la temperatura en un sistema formado por dos fases en equilibrio.
Suponemos un liquido y su vapor en equilibrio a una presión p y temperatura T de modo que en
estas condiciones gv  gl donde g es la función específica de Gibbs.
A una T + dT la presión de vapor es p = dp y las funciones de Gibbs son gv + dgv y gl + dgl .
Sin embargo como el líquido y el vapor están en equilibrio a la nueva temperatura y presión
resulta que los cambios dgv y dgl son iguales
dgv  sv dT  vv dp  sl dT  vl dp  dgl
entonces,
(sv  sl )dT  (vv  vl )dp
v
dp ( sv  sl )


dT (vv  vl ) (vv  vl )T
si estamos lejos del punto triple podemos pensar que vv >> vl entonces obtenemos
dp v

dT vvT
1
y utilizando la ecuación del gas ideal
v

dp
dp

##  ##
 v 2 dT
dT RT T
p RT
p
2.- Objetivos experimentales
o Obtener la curva de equilibrio de las fases líquido-vapor para el agua en las variables
presión temeperatura, es decir, medir la presión de vapor para distintas temperaturas. En
base a estos datos y utilizando la ecuación de Clausius-Clapeyron calcular el calor
latente de vaporización.
o Calcular el calor latente de vaporización a presión atmosférica mediante un método más
directo que el anterior.
3.- Desarrollo Experimental
El práctico se divide en dos partes.
Primera parte:
Elementos utilizados










Recipiente
Botellón
Condensador Liebig
Trampa de agua
Manómetro
Termocupla con su correspondiente visor
Válvulas y mangueras
Mechero Bunsen
Regla calibrada
Sellador
En la figura se puede ver un esquema del dispositivo utilizado.
2
En este equipo se practicó vacío mediante la trampa de agua que se conecta a la canilla de la
red. El botellón sirve como reserva de vacío y para que, si bajase la presión de la red no se
contamine el recipiente con agua de la canilla. El recipiente se llenó con agua destilada hasta un
poco mas da la mitad, además se le colocó una piedrita que jugaba el papel de núcleo de
vaporización. A la salida del recipiente se 0colocó un condensador Liebig cuya función era
evitar que el agua evaporada aumente la presión del sistema, haciéndola regresar al recipiente.
Antes que nada se trato de reducir al máximo las perdidas de vacío del sistema, sellándolo con
Fastix y silicona con la trampa de agua conectada. Así el sellador ingresaba por los orificios
obteniendo un mejor sellado.
Se comienza el experimento bajando lo más posible la presión y se cierra la válvula A. Con el
mechero Bunsen se calienta el agua del recipiente hasta que alcanza el cambio de fase. En este
momento se registran los valores de presión y temperatura mediante el manómetro y la
termocupla. Abriendo un poco la válvula C se dejaba entrar aire para aumentar la presión del
sistema y nuevamente se esperaba la temperatura de cambio de fase.
Segunda Parte:
Elementos utilizados








Recipiente calibrado
Termo
Condensador Liebig
Resistencia calefactora de 60 
Resistencia variable de 300 
Amperímetro
Voltímetro
Cronómetro
En la figura se puede ver un esquema del dispositivo utilizado.
Se llenó el termo con agua destilada y se colocó una resistencia (calentador) conectada a un
circuito que nos permitía medir y regular la potencia entregada a la misma. El termo estaba
sellado y se lo conectó a un condensador el cual goteaba en un recipiente calibrado (de 5 a 25
ml). En un principio se construyó un condensador con una serpentina de cobre para así obtener
3
un mayor intercambio de calor. Pero dada la geometría de esta no se logró obtener un caudal
uniforme y constante, por lo que se decidió utilizar el clásico condensador Liebig.
El agua se calentaba con la resistencia hasta su evaporación, luego se condensaba y goteaba en
el recipiente. Regulando la potencia entregada se buscaba producir un régimen de caudal
constante. Acto seguido se colocaba el recipiente calibrado vacío y mientras este se llenaba se
registraba el tiempo transcurrido y la masa depositada en distintos instantes. Vale aclarar que la
magnitud medida era el volumen en ml y se tomó la densidad del agua igual a 1 gr/ml.
5.- Cálculos
Primera Parte:
A la diferencia de presión medida en el manómetro le sumamos la presión atmosférica, que fue
obtenida del barómetro de Torricelli.
Recordando la ecuación de Clausius-Clapeyron para un cambio de fase líquido-vapor

dp
 v 2 dT
p RT
[1]
integrando, y teniendo en cuenta que en este rango de temperaturas podemos considerar v
constante, obtenemos

ln p   v  C
[2]
RT
por lo tanto graficando ln p en función de 1/T obtendremos una recta con pendiente -v/R y de
aquí despejamos v.
Con los datos obtenidos graficamos la presión de vapor en el plano termodinámico p-T.
Teóricamente, utilizando la ecuación anterior, obtenemos que la curva es de la forma
p  p0e

v
RT
[3]
donde p0 es una condición de contorno que podemos deducir en base a datos obtenidos
experimentalmente, a la presión atmosférica del día de las mediciones, de la siguiente forma
v
p0  pe RT donde p = (102658  400) Pa , v/R = (4843  9) ºK y T = (373,9  1,7) °K
y queda p0 = (4,33  0,38 ) · 1010 Pa
Segunda Parte:
Para evaluar las pérdidas que se presentan en este experimento proponemos que las mismas son
proporcionales al tiempo transcurrido
El balance energético medido es
Pt  Q  q [4]
donde P es la potencia eléctrica suministrada, t es el tiempo transcurrido Q es el calor
necesario para vaporizar una masa m de agua y q es el calor perdido durante el proceso.
Como supusimos que q es proporcional al tiempo y dado que Q =vm resulta
4
Pt  v m  ct ##  ## m 
Pc
v
t [5]
Se pueden observar en el anexo las gráficas de esta función para distintos valores de P. En ellas
se ve claramente la dependencia lineal de la masa evaporada en función del tiempo, lo que
sustenta el modelo supuesto para las pérdidas. Luego con los valores de las pendientes de estas
rectas se obtiene el siguiente sistema de ecuaciones que permite obtener c y v,
 P1  c
   B1
 v

 P2  c  B
2
 v
donde B1 y B2 son las pendientes
despejando obtenemos v 
P2  P1
PB  P B
[6] y c  1 2 2 1 [7]
B2  B1
B2  B1
6.- Tablas y Gráficas
Primera Parte:
Presión atmosférica medida el día de las mediciones: (770  1) mm Hg
Presión
Error
[mm Hg] [mm Hg]
315
3
325
3
338
3
345
3
354
3
366
3
373
3
385
3
394
3
407
3
421
3
431
3
443
3
453
3
463
3
471
3
482
3
491
3
503
3
514
3
524
3
536
3
549
3
560
3
570
3
582
3
Presión
[Pa]
41997
43330
45063
45996
47196
48796
49729
51329
52529
54262
56129
57462
59062
60395
61728
62795
64261
65461
67061
68528
69861
71461
73194
74661
75994
77594
Error [Pa]
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
400
5
Temp
[°C]
77
77,7
78,6
79,1
79,8
80,7
81,3
82,1
82,6
83,3
84,3
85,1
85,7
86,2
86,8
87,4
88,1
88,6
89,2
89,8
90,3
90,9
91,5
92,2
92,6
93,1
Error [°C]
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
593
605
619
631
645
660
671
704
716
729
737
748
758
770
3
3
3
3
3
3
3
3
3
3
3
3
3
3
79060
80660
82527
84126
85993
87993
89459
93859
95459
97192
98259
99725
101058
102658
400
400
400
400
400
400
400
400
400
400
400
400
400
400
93,7
94,1
94,7
95,4
96
96,6
97,1
98,5
99
99,5
99,7
100,1
100,7
100,9
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
1,7
En el anexo se adjuntó una tabla igual a la anterior pero con datos obtenidos de libro.
Gráfica 1 – Ln(p) vs. 1/T, la pendiente de esta gráfica es  v , siendo R la constante universal de los gases
R
El valor de la pendiente es (- 4843  9) ºK, con esto obtenemos los siguientes valores:
v
40264  80
2235  5
[J/mol]
[J/gr]
6
110000
100000
Presión [Pa]
90000
80000
70000
60000
50000
40000
350
355
360
365
370
375
Temperatura [°K]
Gráfica 2 – P vs. T para puntos de equilibrio de fases Líquido-Vapor del agua
110000
100000
Presión [Pa]
90000
80000
70000
60000
50000
Valores Experimentales
Valores Teóricos
40000
350
355
360
365
370
375
Temperatura [°K]
Gráfica 3 – Comparación de P vs. T de la función obtenida teóricamente (ecuación [3]) con los valores tomados
experimentalmente
Segunda Parte:
Los siguientes son los valores de las pendientes obtenidos mediante regresión de la ecuación [5]
para distintas mediciones (las tablas y gráficas de las mediciones se encuentran en el anexo).
7
Medición
1
2
3
4
Potencia [W]
60,0  0,1
75,5  0,1
60,0  0,1
76,2  0,1
Pendiente [gr/s]
0,02381  7 ·10-5
0,03061  10 ·10-5
0,02375  6 ·10-5
0,03085  30 ·10-5
Combinando estos valores armamos los sistemas de ecuaciones [6] y [7] y obtenemos:
v
[J/gr]
c [J/s]
2257  100
2276  100
2276  100
2295  100
6,4  1,5
5,8  1,5
5,9  1,5
5,3  1,5
Vale aclarar que deberíamos obtener seis valores de v haciendo todas las combinaciones
posibles, pero para que los sistemas de ecuaciones tengan sentido no podemos combinar
mediciones hechas con potencias similares, caso de 1 con 3 y 2 con 4.
El valor de v obtenido de libro es 2257 [J/gr]
7.- Conclusión
Podemos ver que el método experimental para obtener la presión de vapor es muy efectivo, ya
que los valores tomados de presión y temperatura coinciden notablemente con los de la curva
obtenida mediante la ecuación de Clausius-Clapeyron y son muy parecidos a los obtenidos de
libro. Hay que recordar que en los intervalos de presión y temperatura en los que trabajamos la
aproximación utilizada sobre la ecuación de Clausius-Clapeyron de despreciar el volumen
específico del líquido respecto del vapor es muy buena.
En cuanto al cálculo de v podemos concluir que ambos experimentos nos dieron resultados
bastante satisfactorios comparándolos con los obtenidos de libro.
Con lo respectivo al armado del experimento podemos comentar el aumento de experiencia en
técnicas de sellado, armado de circuitos eléctricos y conexión de mangueras y válvulas.
8.- Bibliografía

¨ Experimentos De Fisicoquímica ¨ - Urquiza

¨ Trabajos Prácticos De Física ¨ - Fernández Galloni

¨ Fisicoquímica Experimental ¨ – Daniels

¨ Handbook Of Chemistry And Physics ¨
8