DIAGRAMAS DE FASE PARA SISTEMAS DE DOS COMPONENTES

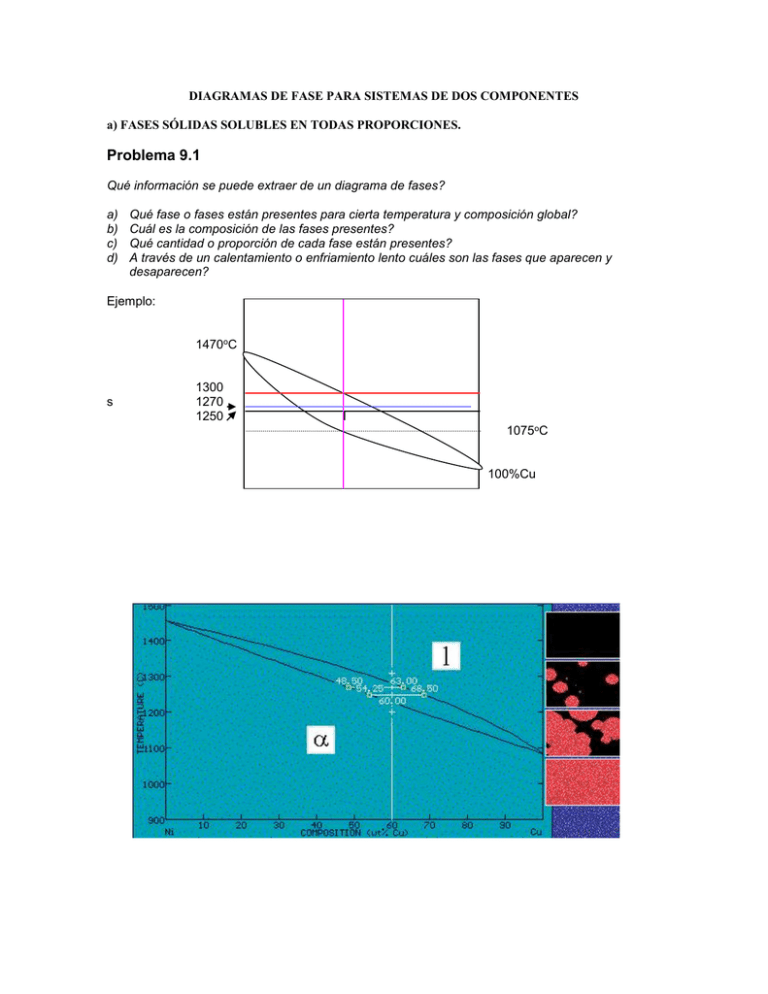
DIAGRAMAS DE FASE PARA SISTEMAS DE DOS COMPONENTES
a) FASES SÓLIDAS SOLUBLES EN TODAS PROPORCIONES.
Problema 9.1
Qué información se puede extraer de un diagrama de fases?
a)
b)
c)
d)
Qué fase o fases están presentes para cierta temperatura y composición global?
Cuál es la composición de las fases presentes?
Qué cantidad o proporción de cada fase están presentes?
A través de un calentamiento o enfriamiento lento cuáles son las fases que aparecen y
desaparecen?
Ejemplo:
Co=60%
1470oC
s
1300
1270
1250
1075oC
Cs=54.25%
CL68,5%
100%Cu
Para aplicar la regla de la palanca debemos considerar que al igual que en los problemas de física
(subibaja) para mantener la palanca en equilibrio
m1 x
L1 = m
2
L2
x
(1)
Cuanto mayor es la masa, menor es la distancia a la que debe estar aplicada respecto del pivote
O.
Si sumamos
m1 (L1 +
m1 x
L2) = (m
2
L2 a ambos miembros de (1)
+ m1)
L2
Entonces también se cumple que:
(2)
m
m m
2
m
m
L
L

1
1
1
totsl

L
2
L1  L2
2
totso
En los diagramas de fase el punto O corresponde a la composición original Co y las masas 1 y 2 a
las masas de las fases sólidas y líquidas respectivamente. Las distancias Li y L 2 corresponden a
las diferencias Co – Cs y CL - Co respectivamente y Ltotsl corresponde a Cs- CL
L1
masa 1
O
L2
masa 2
Vamos a analizar cuál es el cambio en la proporción de fase sólida a medida que la temperatura
asciende.
T=1250oC
El diagrama temperatura/composición para el sistema cobre-níquel (cuyas fases sólidas son
solubles en todas proporciones) indica que para una mezcla con Co= 60% en cobre a 1250 C los
% de fase líquida y sólida son respectivamente: 68.5 % y 54.25 %. Cuál es el porcentaje de la fase
sólida y la líquida a esa temperatura?.
Aplicando la ecuación (2)
m
m
sol
tot
 C L C o  59,65 %
C C
L
s
El % de masa del sólido respecto a la masa total a 1250 C es de 59,65 %
Qué ocurre a 1270 oC
Allí Co = 60%, CL= 63 % y Cs= 48 %
m
m
sol
tot
 C L C o  20,69 %
C C
L
s
Y el % de la masa del sólido respecto a la masa total a 1270 C es de 20,69 %
Vemos entonces en el diagrama que a 1200 oC toda la masa constituye una única fase sólida y a
1300 oC toda la masa constituye una única fase líquida.
Temperatura
Cant. de sólido
1300
1270
1250
1200
0%
20, 69 %
59,65%
100 %
Cantidad de líquido
100%
79,31 %
40,35 %
0%
IMPORTANTE: Debe notarse que a medida que se enfría la cantidad de cobre en el sólido
aumenta a expensas del cobre de la fase líquida.
Problema 9.3
Determine la temperatura de fase líquida, y la temperatura de fase sólida y el intervalo de
temperatura de congelación para las siguientes composiciones del cerámico MgO-FeO
a)
b)
c)
d)
MgO-25 % FeO
MgO -45 % FeO
MgO –60% FeO
MgO- 80 % FeO
a)
b)
c)
d)
Tliq=2590 oC, Tsol= 2250 oC, intervalo de congelación= 2590-2250 oC
Tliq=2330 oC, Tsol= 1920 oC , intervalo de congelación= 2330-1920 oC
Tliq= 2010 oC, Tsol= 1630 oC, intervalo de congelación= 2010-1630 oC
Tliq= 1730 oC, Tsol= 1470 oC, intervalo de congelación= 1730-1470 oC
Problema 9.4
Determine las fases presentes, la composición de cada fase, y la cantidad de cada fase en % para
el cerámico MgO-FeO y 2000 C
a) MgO-25 % FeO
b) MgO- 80 % FeO
a) Si ubicamos el punto correspondiente a 2000 C y 25% FeO observamos que la muestra
corresponde a un sólido con 25% FeO
b)
Co= 45%
CL= 66%
Cs= 40%
En este caso las dos fases están presentes (solución líquida y solución sólida).
La proporción de fase sólida en la masa total está dada por
m
m
sol
tot
 C L C o  80,77%
C C
L
s
Liquido = 1-solido = 19,23 %
Si nos preguntamos cómo es la apariencia de la microestructura, podemos suponer que el área de
cada fase debería corresponder a la fracción de volumen de la misma por lo tanto deberíamos
tener la información de las densidades. Aproximadamente podemos decir que sólo un quinto
(19,23 % peso) de la muestra está como líquido y el resto es sólido.
Aproximadamente como muestra la figura.
c)Consideremos el caso en que la composición original es de 60% . Luego
60%
40 %
m
m
sol
tot
66%
 C L C o  23,08 %
C C
L
s
Líquido= 1-sólido= 76,76 %
Por lo tanto, ahora la mayor proporción es de fase líquida (76,76% peso) y la microestructura sera
del tipo:
d)La muestra es un líquido con 80 % de FeO
Problema 9.5
La aleación Nb-60 p/p W se calienta a 2800 oC. Determine:
a) La composición de las fases sólidas y líquidas en % p/p y % atómico.
b) La cantidad de cada fase en % p/p
c) Suponiendo que la densidad del sólido es de 16,05 g/ml y que la del líquido es de 13,91 g/ml,
determine la cantidad de cada fase en volumen %.
at-g Nb= 92,91 g/mol
at-g W= 183,85 g/mol
Liquido
Del diagrama de fases podemos obtener la información del % de W que hay en las fases sólida y
líquida en equilibrio a 2800 oC para una composición global del 60%.
Para obtener el % atómico tendremos que obtener las relaciones del número de moles de cada
componente respecto all número de moles totales.
Así en la fase sólida
nNb=31/92,91=0,33 mol
y nW = 69/183,85=0.377 mol
luego
nNb /( nNb+ nW ).= 47.06%
y
nW /( nNb+ nW).= 52,94 %
y en la fase líquida sólida
nW =49/183,85=0.266 mol
y nNb= 51/92.91= 0.548 mol
entonces,
nNb /( nNb+ nW).=67,32%
y
nW /( nNb+ nW).= 32,68%
Para determinar la proporción de cada fase utilizamos la regla de la palanca
Fase sólida
masa sol./masa total (%)= (cL - co)/( cL- cs)= 55%
Fase líquida
masa liq./masa total (%)= (cS - co)/( cL- cS)= 45%
c)
Para determinar el % en volumen calcularemos
Vs=volumen de fase sólida=masa f. sol/ densidad sol
Vl=Volumen de fase líquida=masa f. liq/ densidad liq
Vt=Volumen total=Vl + Vs=
Vs%= 51,44%
Vl %= 48,56%
podemos observar que existe una pequeña diferencia con respecto al % en peso (45%,55%)
la microestructura presentará entonces cantidades semejantes de fase sólida y líquida
Problema 9.6
Una aleación Nb-W contiene 55% de la fase alfa sólida a 2600 oC. Determinar:
a) La composición de cada fase
b) La composición global de la aleación
La línea horizontal es la que pasa a través del punto correspondiente a la composición global que
es desconocida.
a) De acuerdo al diagrama la fase sólida en equilibrio tendrá una composición de 42% W y la
líquida contiene 21 %
b) Para determinar la composición de la aleación (Co)
m
m
sol
tot

C C
C C
L
o
L
s
entonces Co= 32.55%
Por lo tanto la aleación tendrá un 32,55 % de Nb y el resto de W.