La de Alberto

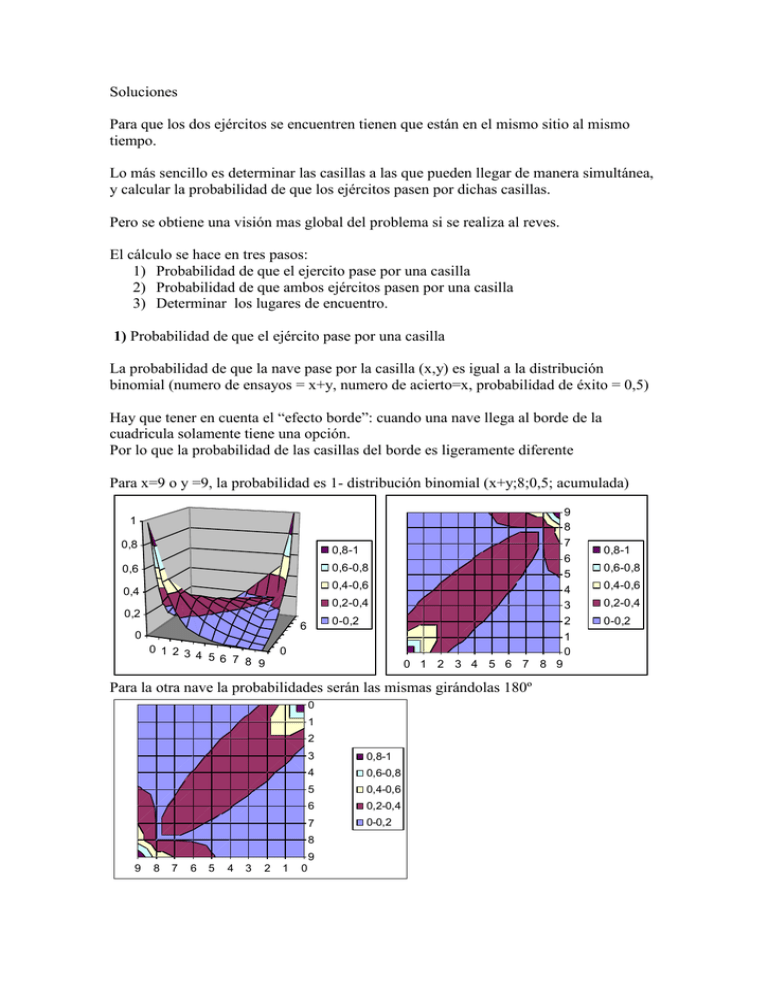
Soluciones
Para que los dos ejércitos se encuentren tienen que están en el mismo sitio al mismo
tiempo.
Lo más sencillo es determinar las casillas a las que pueden llegar de manera simultánea,
y calcular la probabilidad de que los ejércitos pasen por dichas casillas.
Pero se obtiene una visión mas global del problema si se realiza al reves.
El cálculo se hace en tres pasos:
1) Probabilidad de que el ejercito pase por una casilla
2) Probabilidad de que ambos ejércitos pasen por una casilla
3) Determinar los lugares de encuentro.
1) Probabilidad de que el ejército pase por una casilla
La probabilidad de que la nave pase por la casilla (x,y) es igual a la distribución
binomial (numero de ensayos = x+y, numero de acierto=x, probabilidad de éxito = 0,5)
Hay que tener en cuenta el “efecto borde”: cuando una nave llega al borde de la
cuadricula solamente tiene una opción.
Por lo que la probabilidad de las casillas del borde es ligeramente diferente
Para x=9 o y =9, la probabilidad es 1- distribución binomial (x+y;8;0,5; acumulada)
9
8
1
0,8
0,8-1
0,6
0,6-0,8
7
6
5
4
3
2
1
0
0,4-0,6
0,4
0,2-0,4
0,2
0-0,2
6
0
0 1 2 3
4 5 6 7
8 9
0
0 1 2 3 4 5 6 7 8 9
Para la otra nave la probabilidades serán las mismas girándolas 180º
0
1
2
3
0,8-1
4
0,6-0,8
5
0,4-0,6
6
0,2-0,4
7
0-0,2
8
9
9
8
7
6
5
4
3
2
1
0
0,8-1
0,6-0,8
0,4-0,6
0,2-0,4
0-0,2
2) Probabilidad de que ambos ejércitos pasen por una casilla
Multiplicando ambas graficas obtenemos la probabilidad de que las dos casillas
pasen por una casilla determinada. O dicho de otra manera la densidad de
probabilidad de encuentros.
9
0,2
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
0,18-0,2
0,18-0,2
8
0,16-0,18
0,16-0,18
7
0,14-0,16
0,14-0,16
6
0,12-0,14
0,12-0,14
5
0,1-0,12
8
4
0 1 2
3 4 5
6 7 8
9
0
0,1-0,12
4
0,08-0,1
0,08-0,1
0,06-0,08
3
0,06-0,08
0,04-0,06
2
0,04-0,06
0,02-0,04
1
0,02-0,04
0-0,02
0
0-0,02
0
1
2
3
4
5
6
7
8
9
3) Determinar los lugares de encuentro.
Si las dos naves circulan a la misma velocidad, solamente pueden encontrarse sobre la
diagonal equidistante de las dos ciudades.
Representando los valores de las 10 casillas donde se pueden enfrentar los ejércitos
tenemos:
0,07
0,06
0,05
0,04
0,03
0,02
0,01
0
0
1
2
3
4
5
6
7
8
9
Sumando todas las probabilidades obtenemos la primera respuesta 18,54%
Pero si las velocidades son diferentes, no llegaran simultáneamente al diagonal si no a
rectas paralelas a la misma
Hay 19 rectas paralelas a la diagonal. Podemos representándolas todas.
0,3
0,25
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
0,2
0,15
0,1
0,05
18
0
0
2
4
6
8
Sumando los valores de cada recta obtenemos la probabilidad de encuentro cuando los
ejércitos llegan simultáneamente a dicha recta
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
1
2
3
4
5
6
7
8
9 10 11 12 13 14 15 16 17 18
Como puede verse, la probabilidad es prácticamente constante en el centro de la grafica
y crece bruscamente en los extremos.
La llegada simultánea a una determinada recta depende de las velocidades relativas de
las naves. Se puede determinar la probabilidad de encuentro en función de la velocidad
relativa.
probabilidad de encuentro
0,6
0,5
0,4
0,3
0,2
0,1
0
0
5
10
15
20
velocidad relativa
Para que exista una variación significativa en la probabilidad de encuentro, debe existir
una gran diferencia entre sus velocidades.
La probabilidad de encuentro apenas varía su una de las naves es el triple de rápida.
Dependencia con N
50
9
0,1-0,12
25
0,08-0,1
20
3
0,06-0,08
15
2
0,04-0,06
10
1
0,02-0,04
5
0
0-0,02
1
2
3
4
5
6
7
8
9
0,025-0,03
0,02-0,025
0,015-0,02
0,01-0,015
0,005-0,01
0-0,005
0
50
0
0
4
45
0,03-0,035
5
40
30
35
0,035-0,04
0,12-0,14
6
30
35
25
0,04-0,045
0,14-0,16
20
0,16-0,18
7
15
0,045-0,05
40
5
45
8
10
0,18-0,2
Al aumentar N, el “pasillo” de casillas con una probabilidad significativa de ser
recorrido por ambas naves, se hace mas estrecho.
Probabilidad de encuentro
La probabilidad de encuentro disminuye, al aumentar N
0,2
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
0
20
40
60
N
80
100
120
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
0
20
40
60
80
100
La probabilidad de encuentro se mantiene constante en todo el pasillo, solo varia en los
extremos.(Rosa N=10, Azul N=51)
También aumenta velocidad relativa necesaria para conseguir un aumento significativo
en la probabilidad de encuentro:
probabilidad de encuentro
0,6
0,5
0,4
0,3
0,2
0,1
0
0
20
40
60
velocidad relativa
80
100
120
Otras cuestiones interesante:
4) En lugar, de enviar el ejército de una vez, ambos imperios deciden enviar las
naves de una a una. Cada 3 dias una. ¿Qué porcentaje de naves conseguiran
llegar a la ciudad enemiga? ¿Cómo seria la densidad de probabilidad de
encuentros?(El problema es mucho mas complejo de lo que pudiera parecer a
simple vista)
5) Cada imperio fabrica una nave cada 3 dias. Cada nave hace su camino de forma
independiente al resto, pero puede enviarlas al combate en el momento que
estime conveniente. Suponiendo que la guerra la gana el imperio que consiga
llegar primero a la otra ciudad.¿Cual seria la mejor estrategia?¿Enviarlas de una
en una, o acumularlas y lanzarlas simultáneamente en una ola? (Seria un
videojuego relativamente sencillo de programar y muy interesante. ¿Alguien se
anima?)
6) ¿Por qué quedarse en un tablero de 2 dimensiones? Las naves se mueven en 3
dimensiones!!! Cual seria la probabilidad de encuentros si las naves partiese de
los vértices opuestos de un cubo de NxNxN. Si en 2D las naves se encontraban
en 2n-1 rectas paralelas a la diagonal, ahora se encuentran en 3n-1planos
paralelos. Una cada uno de estos planos podemos dibujar una figura que encierre
el 99% de los encuentros producidos en el plano. ¿Qué forma tendrían esas
figuras y como varían a lo largo de los diferentes planos?
7) ¿Por que quedarse en 3 dimensiones? Todo el mundo sabe que las naves
estaciones del dominio escarlata y la Unión Azul pueden moverse en 4
dimensiones. (En realidad en N, pero simplifiquémoslo un poco. “Antes
simplista que incomprensible”). Suponiendo un Hipercubo de NxNxNxN y
partiendo de las aristas opuestas. Las naves se encontraran en 4n-1 espacios
tridimensionales. ¿Qué forma tienen las figuras tridimensionales que engloban
el 99% de los encuentros producidos en cada plano?
8) Si las figuras tridimensionales que encierran el 99% de los encuentros
producidos en un espacio, coinciden con los orbitales del átomo de
hidrogeno.¿Cual es la forma del la figura de 4 dimensiones en la que están
combatiendo las naves? O dicho de otra forma…. ¿Podríamos describir el
comportamiento de los átomos empleando el modelo de nave moviéndose
aleatoriamente en un espacio de 4 dimensiones?