NTP 236: Accidentes de trabajo: control estadístico
Anuncio
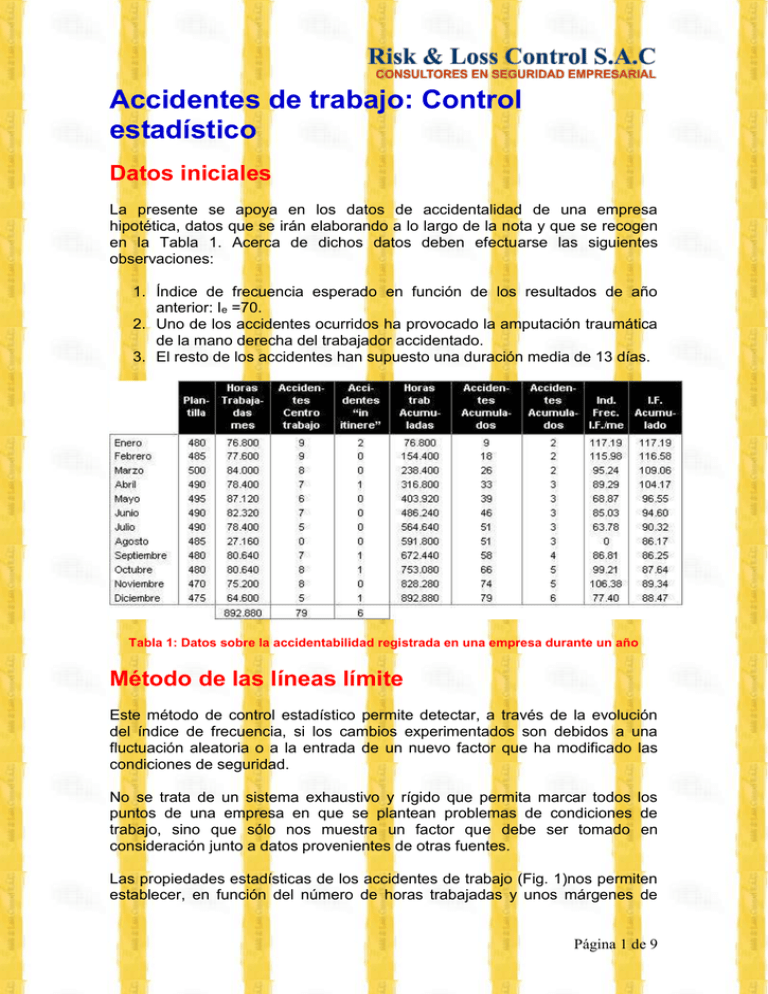
Accidentes de trabajo: Control estadístico Datos iniciales La presente se apoya en los datos de accidentalidad de una empresa hipotética, datos que se irán elaborando a lo largo de la nota y que se recogen en la Tabla 1. Acerca de dichos datos deben efectuarse las siguientes observaciones: 1. Índice de frecuencia esperado en función de los resultados de año anterior: Ie =70. 2. Uno de los accidentes ocurridos ha provocado la amputación traumática de la mano derecha del trabajador accidentado. 3. El resto de los accidentes han supuesto una duración media de 13 días. Tabla 1: Datos sobre la accidentabilidad registrada en una empresa durante un año Método de las líneas límite Este método de control estadístico permite detectar, a través de la evolución del índice de frecuencia, si los cambios experimentados son debidos a una fluctuación aleatoria o a la entrada de un nuevo factor que ha modificado las condiciones de seguridad. No se trata de un sistema exhaustivo y rígido que permita marcar todos los puntos de una empresa en que se plantean problemas de condiciones de trabajo, sino que sólo nos muestra un factor que debe ser tomado en consideración junto a datos provenientes de otras fuentes. Las propiedades estadísticas de los accidentes de trabajo (Fig. 1)nos permiten establecer, en función del número de horas trabajadas y unos márgenes de Página 1 de 9 confianza establecidos, unos valores límites, superiores e inferiores, para el índice de frecuencia deseado, previamente fijado por la empresa, ya sea éste el mismo del año anterior, o bien una determinada reducción del mismo fundada en una política de objetivos de prevención de riesgos laborales. Las propiedades estadísticas de los accidentes de trabajo Los accidentes, estadísticamente hablando, cumplen las siguientes propiedades: Es instantáneo, de tal forma que no se pueden dar dos accidentes simultáneamente. Es decir, se trata de un suceso independiente. El número de 'instantes-hombre' trabajados en un período determinado es un numero muy alto que tiende a infinito. El número de accidentes ocurridos durante un periodo determinado tiende a mantenerse constante para periodos iguales Las probabilidades de ocurrencia del accidente -número de accidentes dividido por el número de 'instanteshombre' trabajados- es, por tanto, muy, pequeña. Este tipo de distribución de probabilidad se ajusta a la distribución de Poisson, en la que la desviación típica es, precisamente, la raíz cuadrada de la media. Fig. 1 Para la aplicación de este método en una empresa se han de considerar tres casos: 1. Si el número de horas trabajadas N, es inferior a 10.000 no es aplicable dicho método, debiéndose acumular las horas de dos o más meses consecutivos. 2. Si el número de horas trabajadas en el período es superior a 10.000, pero inferior a 1.200.000, el intervalo de confianza se determina empleando una Ley de Poisson. 3. Si el número de horas trabajadas en el periodo considerado es superior a 1.200.000, el intervalo de confianza no se encuentra tabulado y Página 2 de 9 deberemos calcularlo aplicando la ley normal, ya que para valores altos la distribución de Poisson se asemeja a la distribución. Criterios para la obtención de los límites superiores e inferiores La tabla 3 anexa nos ofrece los límites superiores e inferiores en función del índice de frecuencia esperado y de las horas trabajadas, hasta un límite de 1.200.000 horas y para un margen de confianza del 90%. Se ha calculado mediante una aproximación empírica que ajusta la fórmula de la distribución normal a la distribución de Poisson, en la que están basadas las tablas originales de P. J. Shipp. La fórmula aplicable para los dos límites en el caso de la distribución normal (ver expresión (1) de la Figura 2) queda reducida, haciendo N'=N /1000 a: Y aproximadamente: La corrección utilizada para aproximarse a los valores de Shipp es: la cual no se ajusta perfectamente a los valores de las tablas mencionadas para valores bajos, pero se aproxima bastante y ofrece una simplicidad de cálculo considerable, siendo, además, válida para cualquier número de horas trabajadas, ya que para N alto el término 750/N' tiende a hacerse despreciable. También nos permite el cálculo de los límites superiores e inferiores para cualquier margen de confianza. Por ejemplo, para el 95% deberemos sustituir el coeficiente 1,65 del desarrollo anterior por 1,96, quedando la desigualdad del siguiente modo: Página 3 de 9 Índice de frecuencia, I = n / N · 106 donde: n = nº de accidentes en un periodo N = nº de horas-hombre trabajadas Siendo la frecuencia f = n / N (número de accidentes por hora trabajada) la media "'m" de accidentes registrados en un período de horas trabajadas "t" será: m=f·t en todo el período N, el numero de accidentes será: m = f x N = n / M x N = I · 10-6 · N Para valores de N altos la distribución de Poisson se ajusta e una distribución Normal con la misma media y con desviación tipo "" igual a Con una probabilidad del 90% la variable estudiada, número de accidentes en el período considerado, estará comprendida en el siguiente intervalo de confianza. m - 1,65 < nº accid. < m + 1,65 sustituyendo valores de "m" multiplicando por 106 / N quedará: y "" y En función del Índice de frecuencia esperado Ie, y del número de horas trabajadas N en uno, dos y tres meses, se determinan los tres límites tanto inferiores como superiores. Figura 2 Página 4 de 9 Cálculo de los índices de frecuencia y gravedad Con los datos de la Tabla 1 deberemos calcular los índices de frecuencia y de gravedad referentes a la accidentabilidad de la empresa durante todo el año. Índice de Frecuencia Número de jornadas perdidas Accidente con amputación traumática mano derecha: 3.000 jornadas Restos de accidentes: 78 accidentes x 13 jornadas perdidas = 1.014 jornadas Total jornadas perdidas: 3.000 + 1.014 = 4.014 jornadas. Índice de gravedad Diagrama índice de frecuencia mes a mes El diagrama mes por mes permite descubrir las fluctuaciones a corto plazo del índice de frecuencia y establecer la significación de un alza repentina. Se trata de representar en un diagrama los índices de frecuencia mensuales, de forma que nos permita interpretar el gráfico en función de la posición de éstos respecto a las diferentes líneas limite. La obtención de los limites (L.S.= límite superior. L.I.= límite inferior) para los tres niveles de sensibilidad se debe hacer mediante las horas trabajadas en un mes para el nivel 1, dos meses acumulados para el nivel 2 y tres meses acumulados para el nivel 3. Estas líneas, obtenidas al inicio de nuestro análisis, nos servirán para todo el período que estudiemos, mientras no varíe de un modo significativo el total de horas trabajadas por mes, ni cambie nuestro índice de frecuencia esperado. Este es el caso de nuestro ejemplo, en el que consideramos las horas de Enero para el nivel 1, las de Enero y Febrero acumuladas para el nivel 2, y las de Enero, Febrero y Marzo para el nivel 3 (Tabla 1). Página 5 de 9 Acudiendo a la tabla 3 anexa, se obtienen los siguentes datos, que se representan en el gráfico 1. Enero Ie=70 Horas trabajadas = 80 x 103L.S.1 = 128 L.I.1 = 31 (se han redondeado por exceso las 76,8 x 103 horas trabajadas de Enero). Enero y Febrero acumulados Ie=70 Horas trabajadas = 160 x 103L.S.2 = 109 L.I.2 = 40 (se han redondeado por exceso las 154,4 x 103 = 76,8 x 103 + 77,6 x 103 horas trabajadas de Enero y Febrero). Enero, Febrero y Marzo acumulados Ie=70 Horas trabajadas = 240 x 103L.S.3 = 101 L.I.3 = 45 (se han redondeado por exceso las 238,4 x 10 3 = 76,8 + 77,6 + 84) x 103 horas trabajadas de Enero, Febrero y Marzo). NOTA.- Al haber tomado las horas trabajadas por exceso obtienen unos límites ligeramente más estrictos, en beneficio de un margen de seguridad. A la vista de la evolución del índice de frecuencia mensual se puede concluir, con un margen de confianza determinado, que las condiciones de seguridad han experimentado una variación significativa si: El índice de frecuencia de un solo mes cae más allá de las rectas 1 (nivel menor de sensibilidad). Los índices de frecuencia de dos meses consecutivos caen más allá de las rectas 2 (nivel de sensibilidad media). Los índices de frecuencia de tres meses consecutivos caen más allá de las rectas 3 (nivel máximo de sensibilidad). Página 6 de 9 Del gráfico 1 se obtienen las siguientes conclusiones sobre la evolución de la accidentabilidad: Gráfico 1: Diagrama mes a mes El índice de frecuencia del mes de enero está dentro de los límites LS1 y LI1 Por tanto, no es necesario adoptar una acción correctora al estar dentro del campo de esperado, con un margen de confianza del 90%. En el mes de febrero se ha producido un empeoramiento considerable de la accidentabilidad fuera del campo de lo esperado, al haberse superado en dos meses consecutivos el límite superior de accidentabilidad LS2. Se debería, adoptar una acción correctora. En el mes de marzo se ha restablecido totalmente la situación anómala del mes anterior, al quedar el índice de frecuencia mensual dentro de los límites fijados, es decir, al no situarse los índices de frecuencia de tres meses consecutivos más allá de la línea LS3. El resto del año, nuestro índice de Frecuencia está siempre dentro de los limites prefijados. Diagrama acumulado El diagrama anual debe permitir el control de las tendencias a largo plazo en el alza o baja de los índices de accidentes. Supongamos que a lo largo de todo un año el índice de frecuencia manifiesta una tendencia constante al alza, o fluctúa durante todo el período por encima del índice de frecuencia esperado. Esto podría ser bastante significativo, aunque los valores del diagrama mes a mes estuvieran dentro de los limites de seguridad. Se calcula para cada mes el índice de frecuencia acumulado, contabilizando los accidentes ocurridos y las horas trabajadas desde el comienzo del período hasta el mes que se estudie. Los límites superior e inferior se determinan para Página 7 de 9 cada mes en función del índice de frecuencia esperado y del total de las horas trabajadas en uno, dos..., hasta doce meses. Con los datos del índice de frecuencia esperado (I e =70) y las horas trabajadas acumuladas, se determinan, los limites superior e inferior, que se reúnen en la tabla 2. Tabla 2: Límites superior e inferior para diagrama acumulado A partir de los datos de la tabla, se trazan las líneas hiperbólicas que delimitan el campo de lo esperado para un margen de confianza del 90%. En el diagrama anual, cuando el índice de frecuencia acumulado sale de los limites fijados por las curvas, se puede pensar que un factor nuevo ha venido a modificar las condiciones de riesgo laboral en la empresa. A la vista de los resultados presentados en el gráfico 2, en el que se han representado los índices de frecuencia acumulados indicados en la Tabla 1, se puede concluir que la evolución de la accidentabilidad ha sido muy desfavorable en el primer semestre. A partir de Julio se aprecia una ligera mejoría, finalizando el año -a partir de Octubre- un poco por encima del limite superior. Ello, bajo un punto de vista estadístico, permite decir que, con un margen de confianza del 90%, el índice de frecuencia obtenido en este año está, generalmente, fuera del límite superior para el índice de frecuencia esperado, establecido al principio del año, aunque el análisis a corto plazo (diagrama mes a mes) sólo nos indicaba una situación anómala en Febrero que se restablecía en Marzo, manteniéndose durante el resto del año dentro de los márgenes. Página 8 de 9 Gráfico 2: Diagrama anual acumulado Vemos, entonces, que efectuar exclusivamente un análisis a corto plazo nos puede conducir al equivoco de una confianza excesiva. Podemos observar que el hecho de mantener de una manera casi constante nuestro índice de frecuencia mensual puede indicar la introducción de un nuevo factor que altere de una manera estable nuestras condiciones de trabajo, aunque el diagrama mes a mes no refleje esta situación. La utilidad del diagrama acumulado está, precisamente, en la indicación de los momentos clave en que se precisa una acción correctora, al salirse el índice de frecuencia del campo de lo esperado. Ello ha sucedido, en el caso analizado, en los meses de Febrero a Julio y Octubre a Diciembre, inclusive. Horas trabajadas 10.000 a 100.00 110.000 a 200.000 210.000 a 300.000 310.000 a 400.000 410.000 a 500.000 510.000 a 600.000 610.000 a 700.000 710.000 a 800.000 810.000 a 900.000 910.000 a 1.000.000 1.010.000 a 1.100.000 Tabla 3 límites superiores e inferiores en función del índice de frecuencia esperado (I e) y de las horas trabajadas, hasta un límite de 1.200.000 horas y para un margen de confianza del 90%. Bibliografía (1) SHIPP, P.J. Presentación y explotación de las estadísticas de accidentes a escala de empresa Nota nº 256. Madrid, Instituto Nacional de Medicina y Seguridad del Trabajo (2) GOMEZ-ACEBO MIRALLES, A. y TORRES GUTIERREZ, V. Control estadístico rápido de los accidentes de trabajo a escala de empresa Nota nº 429. Madrid. Instituto Nacional de Medicina y Seguridad del Trabajo Página 9 de 9