LÍMITES EN EL INFINITO

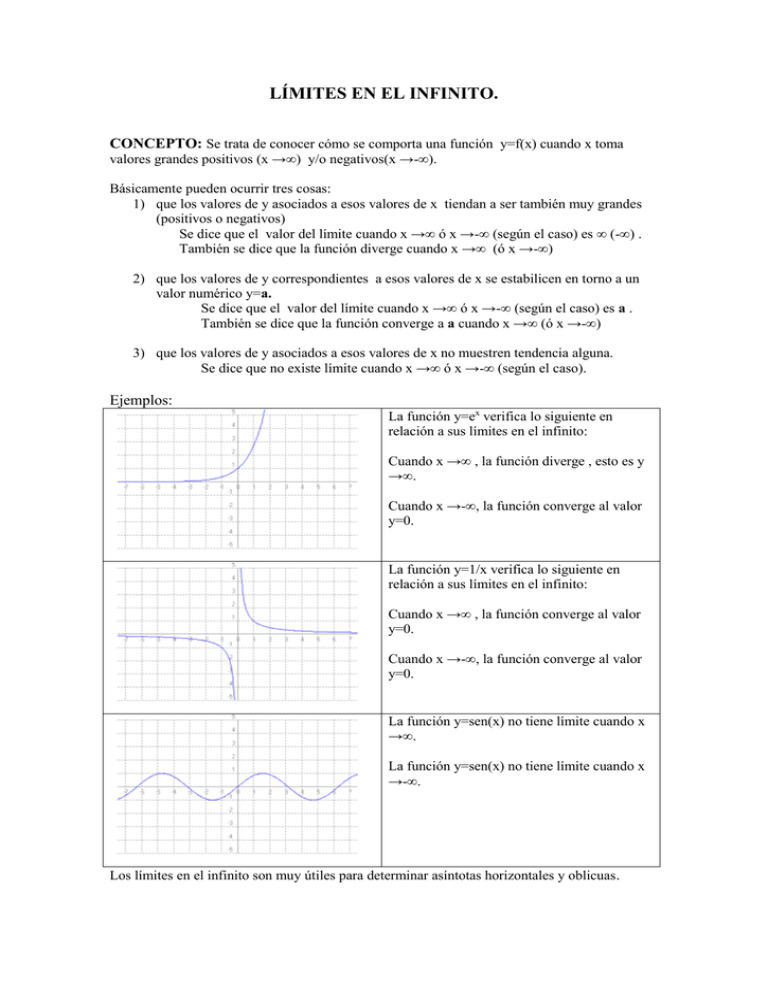
LÍMITES EN EL INFINITO.
CONCEPTO: Se trata de conocer cómo se comporta una función y=f(x) cuando x toma
valores grandes positivos (x →∞) y/o negativos(x →-∞).
Básicamente pueden ocurrir tres cosas:
1) que los valores de y asociados a esos valores de x tiendan a ser también muy grandes
(positivos o negativos)
Se dice que el valor del límite cuando x →∞ ó x →-∞ (según el caso) es ∞ (-∞) .
También se dice que la función diverge cuando x →∞ (ó x →-∞)
2) que los valores de y correspondientes a esos valores de x se estabilicen en torno a un
valor numérico y=a.
Se dice que el valor del límite cuando x →∞ ó x →-∞ (según el caso) es a .
También se dice que la función converge a a cuando x →∞ (ó x →-∞)
3) que los valores de y asociados a esos valores de x no muestren tendencia alguna.
Se dice que no existe límite cuando x →∞ ó x →-∞ (según el caso).
Ejemplos:
La función y=ex verifica lo siguiente en
relación a sus límites en el infinito:
Cuando x →∞ , la función diverge , esto es y
→∞.
Cuando x →-∞, la función converge al valor
y=0.
La función y=1/x verifica lo siguiente en
relación a sus límites en el infinito:
Cuando x →∞ , la función converge al valor
y=0.
Cuando x →-∞, la función converge al valor
y=0.
La función y=sen(x) no tiene límite cuando x
→∞.
La función y=sen(x) no tiene límite cuando x
→-∞.
Los límites en el infinito son muy útiles para determinar asíntotas horizontales y oblicuas.
CÁLCULO DE LÍMITES EN EL INFINITO.
ARITMÉTICA CON ∞:No debéis olvidar que ∞ representa un número muy grande.Por
tanto es lógico el cumplimiento de las siguientes reglas cuando nos enfrentamos a operaciones
en las que entre en juego el citado símbolo.
SUMAS
→∞+→∞=→∞
K + →∞ =→∞
K + → - ∞ =→ - ∞
PRODUCTOS 1
→∞.→∞=→∞
→ (-∞).→ (-∞)=→∞
→∞.→ (-∞)=→(-∞)
PRODUCTOS 2
→K. →∞=→∞ si K>0
→K. →∞=→(-∞) si K<0
→K. → (-∞)=→(-∞) si K>0
→K. → (-∞)=→∞ si K<0
DIVISIONES 1
(→0+) alude a una función que se aproxima a la recta y=0 (eje X) desde valores
positivos cuando x→∞ ó x→-∞
(→0-) alude a una función que se aproxima a la recta y=0 (eje X) desde valores
negativos cuando x→∞ ó x→-∞
→K/(→0+) =→∞ si K>0
→K/(→0+) = →(-∞) si K<0
→K/(→0 ) =→∞ si K<0
→K/(→0-) = →(-∞) si K>0
DIVISIONES 2
→K/ (→∞) =→0 (para cualquier K). ACTIVIDAD: Aclara como tiende a
cero este cociente según el valor de K. Idem con →K/ (→- ∞) = →0
POTENCIAS 1
(→∞)→∞ = →∞
(→∞)→ - ∞ = 0
POTENCIAS 2
→K→∞=→∞ (con K>0,K≠1)
→K→ - ∞=→0 (con K>0,K≠1)
INDETERMINACIONES:Determinadas operaciones no tienen un resultado claro cuando
aparecen el símbolo ∞.Estas situaciones se denominan indeterminaciones.
→∞/→∞
→(-∞)/→∞
→∞/→(-∞)
→(-∞)/→(-∞)
→0+.→∞
→0+.→(-∞)
→0-.→∞
→0-.→(-∞)
→∞ - →∞
→1→∞
1→ - ∞
IMPORTANCIA DE FUNCIONES PARA VALORES DE x→∞
El cálculo de límites cuando x→∞ ó x→-∞ se simplifica si conocemos la importancia
de los diferentes tipos de funciones con esos valores. De mayor a menor importancia
nos encontramos las siguientes funciones.
cuando x→∞
Cuando x→-∞
y= ax
(si a >1)
y= ax(si
0<a <1)
y=xa
(a >0)
y=xa
(a >0)
y=logax y= K
(a >1)
y= K
y=xa
(a<0)
y=xa
y= ax
(a<0)
(si 0<a <1)
x
y= a
(si a >1)
PROCEDIMIENTOS DE CÁLCULO DE LÍMITES EN EL INFINITO.
1.- Gráfico
2.-Numérico
3.-Analítico.
MÉTODO ANALÍTICO. Algunos ejemplos.
Límites en el infinito de f(x) 
x1
x2  1
x→∞
En el denominador x2+1 es mucho más importante el sumando x2 que 1. Por tanto podemos
deshacernos de éste último para el estudio del comportamiento de la función.
En el numerador ocurre algo parecido con x y -1 (se impone x).
f(x) en esas circunstancias se transforma en f(x)= x/ x2 y haciendo uso de nuestros
conocimientos de operaciones con potencias eso es igual a g(x)=1/x. De acuerdo a las reglas de
la aritmética con ∞ , 1/x se transforma en una expresión del tipo →1/ (→∞) y eso tiende a 0+.
Por tanto este límite es igual a 0 (aproximándonos a ese valor con números positivos)
x→ - ∞
En el denominador x2+1 es mucho más importante el sumando x2 que 1. Por tanto podemos
deshacernos de éste último para el estudio del comportamiento de la función.
En el numerador ocurre algo parecido con x y -1 (se impone x).
f(x) en esas circunstancias se transforma en f(x)= x/ x2 y haciendo uso de nuestros
conocimientos de operaciones con potencias eso es igual a g(x)=1/x.De acuerdo a las reglas de
la aritmética con ∞ , 1/x se transforma en una expresión del tipo →1/ (→ -∞) y eso tiende a 0-.
Por tanto este límite es igual a 0, (aproximándonos a ese valor con números negativos).
Límites en el infinito de f (x) 
x 2
x 4
x→∞
En el numerador x+2 es más importante el factor x que el 2. En el denominador x-4 es más
importante el sumando x que -4. El radicando de f(x) en esas circunstancias se transforma en x/x
, es decir 1. Por tanto f(x) se comporta en x→∞ como la raiz cuadrada de 1 y su límite es por
tanto 1.
x→ -∞
Mismo razonamiento que para x→∞ .
Límites en el infinito de g(x) 
x3
x2  1
x→∞
En el denominador el sumando x2 es mucho más importante que 1. Por tanto g(x) se convierte
en x3/x2 que es igual a x. Por tanto el límite es ∞
.
x→ -∞
En el denominador el sumando x2 es mucho más importante que 1. Por tanto g(x) se convierte
en x3/x2 que es igual a x. Por tanto el límite es - ∞
.
Límites es el infinito de f (x) 
x3  1
x3  2 x 2  3 x
 x2  9
x→∞
La función f(x) consta de dos sumandos. El primero es una fracción de polinomios y el segundo
una raíz de un polinomio de segundo grado.
En la fracción de polinomios , el término más importante del numerador es x3, y en el
denominador x3. Por tanto ese sumando en x→∞ se transforma en x3/ x3 que es igual a 1.
En la raíz se verifica que el término más importante del radicando es x2 que cuando x→∞ toma
también el valor ∞ . Como la raíz cuadrada de ∞ es ∞ ., éste es el valor del segundo sumando.
El límite de la suma de las dos partes se obtiene sumando los dos resultados anteriores. →1+
→∞ = →∞
x→-∞
En relación al primer sumando vale lo indicado anteriormente.
En la raíz se verifica que el término más importante del radicando es x2 que cuando x→ ∞toma también el valor ∞ (un número negativo elevado al cuadrado es positivo). Como la raíz
cuadrada de ∞ es ∞ , éste es el valor del segundo sumando.
Al igual que lo indicado anteriormente, el límite de la suma de las dos partes se obtiene
sumando los dos resultados anteriores. →1+ →∞ = →∞.
Límites en el infinito de
x→∞
En el numerador el sumando x4 es mucho más importante que 1. Por tanto f(x) se convierte en
x4/x2 que es igual a x2. Por tanto el límite es ∞ .
x→ -∞
Válido lo explicado en el apartado anterior. No se debe olvidar que un valor negativo
elevado al cuadrado tiene signo positivo.
 x  1
.
x  2
Límites en el infinito de y = ln 

x→∞
En el interior del paréntesis en el numerados y el denominador el factor más importante es la x.
Por tanto ese paréntesis en x→∞ equivale a x/x , es decir a 1. Como ln 1=0 , éste es el valor del
límite.
x→- ∞
Mismo razonamiento que el caso anterior. Observar que no hay problemas de dominio puesto
que tanto numerador y denominador en esta “zona” son negativos y por ello el resultado del
cociente es positivo.
Límites en el infinito de
x→∞
Usando lo que sabemos acerca de exponentes negativos la función f(x) se transforma en (x-1)/
ex . En el numerador el término más importante es x. Por tanto esa función se comporta en
x→∞ como x/ ex . Llegamos a una indeterminación del tipo →∞/→∞ que se resuelve
fácilmente teniendo en cuenta que la función x es menos importante que ex
Por ello el límite es 0.
x→∞
Por la misma razón que antes esta función se comporta como x/ ex. La indeterminación
→∞/→∞ se resuelve en esta zona de otra forma ya que la función x ahora es más importante.
Haciendo uso de los signos el límite es - ∞.