Sea una función,

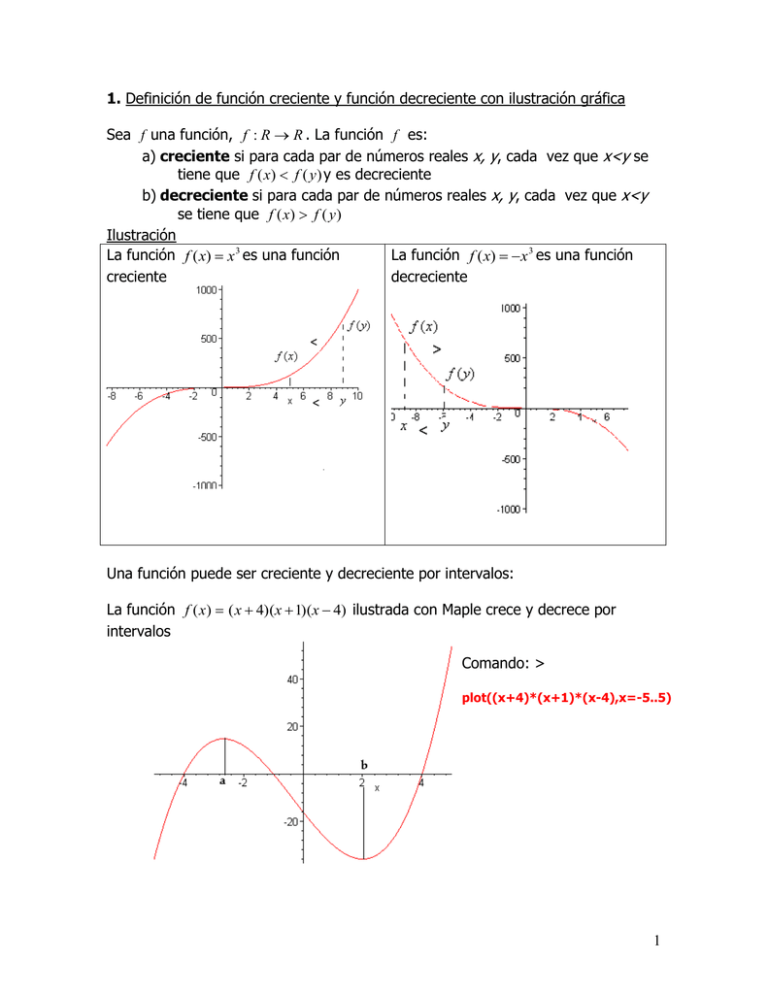
1. Definición de función creciente y función decreciente con ilustración gráfica
Sea f una función, f : R  R . La función f es:
a) creciente si para cada par de números reales x, y, cada vez que x<y se
tiene que f ( x)  f ( y ) y es decreciente
b) decreciente si para cada par de números reales x, y, cada vez que x<y
se tiene que f ( x)  f ( y )
Ilustración
La función f ( x)  x 3 es una función
La función f ( x)   x 3 es una función
creciente
decreciente
Una función puede ser creciente y decreciente por intervalos:
La función f (x)  ( x  4)(x  1)(x  4) ilustrada con Maple crece y decrece por
intervalos
Comando: >
plot((x+4)*(x+1)*(x-4),x=-5..5)
1
La función es creciente en los intervalos  , a , b,  y decreciente en a, b
2. Teorema de Rolle
Si:



f es una función continua definidas en un intervalo cerrado [a, b]
f es derivable sobre el intervalo abierto (a, b)
f(a) = f(b)
Entonces: existe un número c en el intervalo (a, b) tal que f '(c) = 0 .
Ilustración: Dos ejemplos en un sólo gráfico
Ejemplo I
La función graficada arriba es f (x)  ( x  4)(x  1)(x  4) = x 3  x 2  16x  16 .
Si tomamos a = -4 y b = -1, tenemos que f (a)  f (b)  0 . A partir de
f ( x)  3x 2  2x  16 = 0, encontramos que x  2.67 , es el x que pertenece a
 4,1 que satisface el teorema de Rolle.
Aun cuando no es necesario que f(a) = f(b) = 0, hemos escogido estos puntos
por que de antemano sabemos que en ellos f(a) = f(b).
Ejemplo II
Del mismo modo. Como f (1)  f (4) , al resolver de nuevo
f ( x)  3x 2  2x  16  0 , obtenemos la raíz positiva x  2 , que corresponde al
valor de x que satisface el teorema de Rolle en el intervalo  1,4
2
3. Teorema del Valor Medio. El teorema de valor medio dice que si f es una
función definida y continua [ a , b ] y diferenciable en el intervalo abierto ( a , b )
entonces existe al menos algún punto c en el intervalo ( a , b ) tal que la tangente
a la curva en c es paralela a la recta secante que une los puntos (a, f(a)) y
(b, f(b)).
Ilustración
Ejemplo I. Verificación gráfica del teorema del valor medio para la función
f ( x)  x  4x  4x  1 en el intervalo  4,6
f (6)  f (4) 140  0

 14
6  (4)
10
Como f ( x)  x  4x  4x  1= x 3  x 2  16x  16 , entonces f ( x)  3x 2  2x  16 .
Para hallar el punto c , -4 < c < 6 , que satisface el teorema del valor medio
debemos resolver la ecuación:
La pendiente de la recta secante es m 
f ( x)  3x 2  2x  16 = 14. Resolviéndola por la formula de segundo grado,
hallamos que la solución positiva corresponde a c = x  2,85 , que coincide con la
respuesta que sugiere el gráfico anterior.
3
Ejemplo II. El grafico siguiente obtenido con Maple

plot(10*x^4,x=-1..10);
nos permite apreciar el comportamiento de la función f ( x)  x 4 , en el intervalo
4,10
f (10)  f (4) 100000  2560

 16.420
10  4
6
Ahora f ( x)  40x 3 . Para hallar el punto en el cual la recta tangente es paralela a
la recta secante, debemos resolver f ( x)  40x 3 =16.420. Con ayuda de una
calculadora se halló x  7,43, coincide con el punto sugerido geométricamente por
el gráfico anterior.
La pendiente de la secante es m 
4. Teorema: Sea f una función continua en un intervalo I y diferenciable en todo
punto interior de I.
1. Si f ( x)  0 en todo punto interior de I, entonces f es creciente en I.
2. Si f ( x)  0 en todo punto interior de I, entonces f es decreciente en I.
Ejemplo I
Sea
f x  3x 2  x
f ( x)  6 x  1
Resolviendo: f ( x)  6 x  1 > 0 ,
1
Encontramos: x  
6
Por lo tanto la función es creciente en
 1 
el intervalo   ,   , como lo indica
 6 
la figura de la izquierda
4
Ejemplo II:
Sea
f x  3x 2  x
f ( x)  6 x  1
Resolviendo: f ( x)  6 x  1 < 0 ,
1
Encontramos: x  
6
Por lo tanto la función es creciente en
1

el intervalo   ,  , como lo
6

indica la figura de la izquierda
5. Probar que la siguiente función es creciente (en todo su dominio)
1a. f ( x)  2 x  5
f ( x)  2
Como f x  0 , la función es creciente en todo su dominio
Hallar los intervalos de crecimiento y decrecimiento de las funciones dadas y
bosquejar el grafico de las funciones:
3. f ( x)  x2
f ( x)  2 x .
a)
b)
0, 
Como 2x>0 para todo x>0, tenemos que f es creciente en el intervalo
Como 2x<0 para todo x<0, tenemos que f es decreciente en el intervalo
 ,0
5
Gráfico:
6. y  ( x  2) 3
Como y  3( x  2) 2  0, x  R , concluimos que la función es creciente en todo
su dominio.
Gráfico:
7. f ( x)  x 3  3x  1 . Luego f ( x)  3x 2  3  3( x 2  1) .
Como x 2  1  0 en el intervalo  1, 1 , la función f es decreciente en  1, 1 ,
fuera de  1, 1 , se tiene que x 2  1  0 , por lo tanto la función f es creciente
en  ,1  1, 
12. q ( x ) 
x
x2
6
x2 x
2

 0 , x  R, x  2 , concluimos que ni la
2
( x  2)
( x  2) 2
función, ni la primera derivada existen en x=2, y que en cualquier otro lugar, la
función es decreciente.
Calculando q( x) 
Gráfico
6. Definición de máximos y mínimos relativos
Una función tiene un máximo relativo o máximo local en un punto c, si existe un
intervalo abierto contenido en el dominio de f , que contenga a c , tal que
f (c)  f ( x) para todo x en el intervalo abierto.
Por ejemplo, la función f (x)  ( x  4)(x  1)(x  4) = x 3  x 2  16x  16 , al graficarla,
presenta un máximo y un mínimo relativos, como se ve en el gráfico:
Los puntos de Máxima y mínima se han señalado con las letra M y m. Los
extremos de los intervalos a los que se refiere la definición no se han calculado,
pero si escogido convenientemente.
7
7. Teorema 6.4
Si la función f tiene un extremo relativo en c y si existe f (c ) , entonces f (c)  0
Ejemplo I:
El gráfico de la función f (x)  ( x  4)(x  1)(x  4) = x 3  x 2  16x  16 , muestra los
extremos relativos, en donde f (c)  0 , es decir: la pendiente de la recta tangente
es 0.
Ejemplo II
La función f ( x)  ( x  1) 2  10 que se presenta en la gráfica siguiente, por razones
obvias, tiene un máximo de y = 10 en x =1. Allí la pendiente de la recta tangente
es 0.
8
8. Punto crítico
Definición: Un punto c en el dominio de una función f es un punto crítico si
f (c)  0 o f (c ) no existe.
Ejemplo I
El dominio de la función f ( x)  x 2  1 es  ,1  1,  . Como f ( x) 
x
x 1
2
,
concluimos que:
f ( x) 
x
f ( x) 
x
= 0  x= 0. Sin embargo x= 0, no es un punto crítico ya que no
x2 1
pertenece al dominio de f .
no existe cuando x= 1 o x= -1. Como estos puntos si pertenecen
x2 1
al dominio de f , estos son los únicos puntos críticos.
Ejemplo II
El dominio de la función f ( x)  sen x es todo R.
Como f ( x)  cos x cuyo dominio es también R, los únicos puntos críticos son del
tipo f ( x)  cos x = 0.
Estos puntos son de la forma k , k  Z
9. Criterio de la primera derivada para extremos relativos
Sea f una función continua en un intervalo (a, b) y sea c  (a, b) un punto crítico
de f .
a) Si f ( x)  0 en un intervalo abierto a la izquierda de c y si f ( x)  0 en
un intervalo abierto a la derecha de c , entonces f tiene un máximo
relativo en c.
b) Si f ( x)  0 en un intervalo abierto a la izquierda de c y si f ( x)  0 en
un intervalo abierto a la derecha de c , entonces f tiene un mínimo
relativo en c.
9
c) Si en un intervalo abierto a la izquierda de c y en un intervalo abierto a
la derecha de c , f (x) tiene el mismo signo, entonces f no tiene un
máximo ni un mínimo relativo en c.
Ejemplo I
La función f ( x)  x 2 , es tal que f ( x)  2 x  0 en (,0) y f ( x)  2 x  0 en
(0, ) , luego por el criterio b) tiene un mínimo relativo en x  0 .
Ejemplo II
La función f ( x)  x 3 es tal que f ( x)  3x 2  0 tanto en (,0) como en
(0, ) , luego por el criterio c) no tiene ni máximo ni mínimo relativo en x  0 .
10. Máximos y mínimos absolutos
a) Sea f una función y sea A un subconjunto del dominio de f. Diremos
que f tiene un máximo absoluto ( o simplemente un máximo)
sobre el conjunto A, si existe c  A tal que f (c)  f ( x) , x  A. El
número f (c) recibe el nombre de valor máximo de f sobre A.
b) Sea f una función y sea A un subconjunto del dominio de f. Diremos
que f tiene un mínimo absoluto ( o simplemente un mínimo) sobre
el conjunto A, si existe c  A tal que f (c)  f x  , x  A. El
número f (c) recibe el nombre de valor mínimo de f sobre A.
Estos valores se denominan también extremos absolutos.
Ejemplo I
La función del gráfico correspondiente a f ( x)  x 2 tiene un mínimo absoluto
en A= 0,2 , f (0)  0 en x= 0 y un mínimo absoluto f (2)  4
10
Ejemplo II
La misma función f ( x)  x 2 , tiene un mínimo absoluto f (0)  0 en R, mas no
tiene máximo absoluto en R.
11. Teorema del valor extremo (Llamado también Teorema de Weierstrass )
Si f es una función continua en un intervalo cerrado a, b entonces f tiene un
máximo absoluto y un mínimo absoluto en a, b .
Ejemplo I
La función continua del gráfico que corresponde a
f (x)  ( x  4)(x  1)(x  4) = x 3  x 2  16x  16 , tiene un máximo absoluto en
 4,2 y un mínimo absoluto en 0,4
11
Ejemplo II
Tomando el intervalo  2,2, para la función continua
f (x)  ( x  4)(x  1)(x  4) = x 3  x 2  16x  16 ,
Obtenemos los valores máximo y mínimo absolutos en los extremos del intervalo.
12. Problemas Propuestos Resueltos
En los problemas siguientes hallar los puntos críticos y los extremos relativos.
2.
1
f ( x)   x 2  4 x  2
3
2
Luego f ( x)   x  4
3
2
Puntos críticos: f ( x)   x  4 =0  x  6
3
Estudio de primera derivada
Analizando los cambios de signo de la primera derivada en el punto crítico,
concluimos que el valor f (6)  10 es un máximo relativo.
Observemos el gráfico de la función alrededor de x=-6, efectuado con Maple
12
3.


Luego g ( x)  6 x 2  6 x  12= 6 x 2  x  2 (1)
g ( x)  2 x 3  3x 2  12x  5
Las raíces de (1) son -1 y 2. Estos son puntos críticos.
Analicemos el cambio de signo de las derivadas en los puntos críticos
Los puntos críticos de la función son x1  1 y
de g ( x)  12 y mínimo relativo g ( x)  15
x2  2 , con valor máximo relativo
Veamos el gráfico de la función hecho con Maple:
13
5.
g ( x)   x 3  12x 2  36x
Por lo tanto g ( x)  3x 2  24x  36 . Los puntos críticos a partir de g ( x)  0 son
x1  2 y x2  6 .
El análisis del cambio de signo de las derivadas se presenta en el siguiente gráfico:
Los valores extremos son mínimo relativo g (2)  32 y máximo relativo g (6)  0
Comparemos los resultados con el gráfico hecho con Maple
x
1
. Por lo tanto f ( x) 
x 1
x  12
El único posible punto crítico es x  1 , donde f (x) no existe, mas por no
pertenecer al dominio de la función, no se considera un punto crítico. No hay
1
puntos críticos. Como f ( x) 
> 0 , x  R , la función siempre es creciente
x  12
en su dominio.
16.
f ( x) 
Esta función un poco difícil de generar con Maple tiene una asíntota vertical en
x = 1.
14
x2
x( x  2)
. Operando algebraicamente se concluye que f ( x) 
x 1
( x  1) 2
Los únicos puntos críticos son x1  0 y x2  2 , ya que x = 1, no pertenece al
dominio de la función.
17. f ( x) 
Estudiando los diagramas de cambio de signo que se presentan en la siguiente
figura, extraeremos nuestras conclusiones.
La función no se ve bien con Maple, el cual si prresenta la asíntota vertical en x =1
. Para ver los valores extremos es necesario ordenarle a maple que grafique por
segmentos así:
15
> plot (x^2/(x-1),x=-1..0.5);
Aquí se puede apreciar el valor extremo máximo en x = 0
Graficando cerca de x = 2, vemos la situación como quien mira con lupa:
> plot (x^2/(x-1),x=1.5..2.5);
Apreciándose el valor extremo mínimo en x = 2.
13. Concavidad
Definiciones
El gráfico de una función es cóncavo hacia arriba, si el gráfico está siempre encima
de cualquier recta tangente; y es concavo hacia abajo si el gráfico está siempre
por debajo de cualquier recta tangente
16
Ilustración
Cóncava hacia arriba
Cóncava hacia abajo
14. Criterio de Concavidad
Si para a < x <b
f ( x)  0
f ( x)  0
El gráfico de f en (a, b) es
Cóncavo hacia arriba
Cóncavo hacia abajo
Ejemplo I
f ( x)  x 4  4 x 3  10 . Por lo tanto f ( x)  4x 3  12x 2  4x 2 ( x  3)
f ( x)  12x 2  24x  12x( x  2) .
Los cambios de signo de la segunda derivada se dan en la recta en referencia a las
raíces o ceros de la segunda derivada, soluciones de f ( x)  0 , los cuales se
ilustran en el siguiente gráfico.
17
Por lo tanto concluimos que el gráfico es cóncavo hacia arriba en  ,0 y 2, 
y cóncavo hacia abajo en (0,2) . Examinemos estas concavidades graficando con
Maple
El cambio de concavidad en x = 2 es bastante sutil.
Ejemplo II
Sea f ( x)  sen x . Luego f ( x)  cos x y f ( x)  sen x
Los signos de f ( x)  sen x se pueden ver revisando los cuadrantes en el circulo
trigonométrico.
18
Se ve por lo tanto que la función es cóncava hacia abajo entre 0 y  y cóncava
hacia arriba entre  y 2  .
Veamos esta situación con Maple. Hemos llenado en color gris las concavidades
hacia abajo, tal como se hizo en el círculo anterior.
15. Punto de inflexión
Definición
Un punto de inflexión en un gráfico, es un punto donde la gráfica cambia de
concavidad.
19
Ejemplo I
La gráfica de y  x 3 , tiene un punto de inflexión en x=0, y=0.
Veamos el gráfico en el cual hemos marcado las concavidades con color gris.
Ejemplo II
La función f ( x)  x(12  2x) 2 tiene un punto de inflexión muy sutil para un valor de
x entre 3 y 5, como lo sugiere el gráfico de Maple.
> plot(x*(12-2*x)^2,x=0..6);
20
16 Criterio de la segunda derivada para extremos relativos
Si
f (c)  0
f (c)  0
Y si
f (c)  0
f (c)  0
Entonces f tiene
Un mínimo relativo en c
Un máximo relativo en c
Ejemplo I
x4
 2 x 2  4 , f ( x)  x 3  4 x y f ( x)  3x 2  4
Para la función f ( x) 
4
Los puntos críticos para los cuales f ( x)  x 3  4 x = 0 son x1  2 , x2  0 , x3  2
De allí la tabla siguiente:
x = -2
x=0
x=2
f (2)  0
f (0)  0
f (0)  4
f   (2)  8
f (0)  4
f (2)  8
Mínimo relativo
Máximo relativo
Mínimo relativo
f (2)  0
f (0)  4
f (2)  0
Este análisis concuerda con la figura graficada con Maple
Ejemplo II
La función f ( x)  3( x  1) 2  10 , es tal que f ( x)  6( x  1) y f ( x)  6  0 , indicando
que en todos los puntos críticos con f ( x)  0 , hay un mínimo relativo. Como el
único punto crítico de este tipo es x = 1, tenemos allí un valor mínimo, f (1)  10 ,
como se puede verificar en el gráfico siguiente.
21
17. Pasos para dibujar el gráfico de una función
Paso 1 Efectuar un análisis de continuidad y discontinuidad, examinando límites
laterales de ser necesario.
Paso 2. Hallar las intersecciones con los ejes
Paso 3. Estudiar la primera derivada
Paso 4. Estudiar la segunda derivada
Paso 5. Esbozar el gráfico
Paso 6. Graficar la función
1
x 1
Paso 1. Análisis de continuidad y discontinuidad.
La función es discontinua en x = 1, ya que allí el divisor da 0. examinaremos los
límites laterales en el punto de discontinuidad:
Ejemplo I. Graficaremos f ( x ) 
lim f ( x)  
y
lim f ( x)  
x  1
x  1
punto de discontinuidad x = 1.
, indicando que hay una asíntota vertical en el
Paso 2. Intersecciones con los ejes.
Intersección con el eje y: x = 0. Es decir, se da en y = -1.
Intersección con el eje x: y = 0. En este caso, tal valor de x no existe. Ello se debe
a que hay una asíntota horizontal ,ya que cuando x  , y  0  , y cuando
x  , y  0  . Esto demuestra que el eje y = 0, es una asíntota vertical. No hay
intersección con el eje x.
22
Paso 3. Estudiar la primera derivada
Estudio de f (x)
1
. No hay puntos críticos del tipo f ( x)  0
( x  1) 2
1
Como f ( x)  
< 0, para todo x, la función es decreciente, salvo en el
( x  1) 2
punto de discontinuidad x= 1.
No hay puntos críticos por indeterminación de la primera derivada, ya que el único
posible, x = 1 , no pertenece al dominio de la función.
f ( x)  
Paso 4. Estudio de la segunda derivada
2
2
es tal que a) f ( x) 
< 0, si x < 1. Luego la función es
f ( x) 
3
( x  1)
( x  1) 3
cóncava hacia abajo en  ,1
2
Dado que f ( x) 
> 0, si x > 1, la función es cóncava hacia arriba en 1,  
( x  1) 3
Pasos 5: Efectuar un bosquejo
Paso 6. Graficar
La función no es fácil de graficar con precisión, como nos lo muestra Maple.
23
> plot(1/(x-1), x=-20..20);
Ejemplo II
Procederemos a efectuar el gráfico de la recta y = -3x +2
Paso 1. Análisis de continuidad y discontinuidad.
La función no tiene discontinuidades.
Paso 2. Intersecciones con los Ejes
Intersección con el eje Y: x = 0. Por lo tanto y = 2
2
Intersección con el eje X: y = 0. Por lo tanto x =
3
Paso 3. Estudiar la primera derivada.
Como f(x) = - 3x + 2, entonces f´(x) = -3. La función es siempre decreciente y no
hay cambios de signo en la primera derivada, lo cual sugiere que no hay puntos
críticos, ni máximos ni mínimos relativos.
Paso 4: Estudiar la segunda derivada
En este caso f´´(x) = 0. Lo cual no nos permite aplicar ese criterio para estudiar la
concavidad. Por supuesto que la recta no es cóncava hacia arriba ni hacia abajo.
Paso 5 Efectuar un bosquejo
Procederemos por su sencillez a dibujar la recta basandonos en los puntos de corte
con los ejes. Pero utilizaremos Maple para verificar nuestros resultados
24
18 Problemas Propuestos Resueltos
Graficar las funciones siguientes
20.
f ( x)  x 3  6x 2  9x  1
Corte con el eje Y: x= 0, luego y = 1
Estudiemos las derivadas f ( x)  3x 2  12x  9 , f ( x)  6 x  12
Raíces de la segunda derivada: f ( x)  6 x  12 = 0, x1  2
Puntos críticos: Donde f ( x)  3x 2  12x  9 = 3( x 2  4x  3)  3( x  1)(x  3)  0
Por lo tanto x1 = 1, x2 = 3
El gráfico del comportamiento de la primera derivada es:
Valores importantes: f (1)  5 , f (3)  1
Respuestas estudiando el comportamiento de la segunda derivada
X<2
f ( x)  6 x  12
<0
Concavidad
Abajo
Punto de inflexión: f (2)  3
2
0
Inflexión
2<x
>0
Arriba
25
Sabemos además que
f ( x)  
x  
y
f ( x)  
x
Un bosquejo del gráfico sería:
El gráfico realizado con Maple es:
21 f ( x)  x 4  2x 2  1,
Cortes con los ejes
Corte con el eje Y; x=0, y 1
Cortes con el eje X, cuando f ( x)  x 4  2x 2  1= ( x 2 ) 2  2 x 2  1  ( x 2  1) 2  0
Las raíces son x1  1 y x2  1
Luego f ( x)  4x 3  4x y f ( x)  12x 2  4
Puntos críticos: f ( x)  4x 3  4x = 4 x( x 2  1)  0 . Por lo tanto
x1  1 , x2  0 , x3  1
Estudio gráfico de los signos de la primera derivada
26
Raíces de la segunda derivada:
3
3
, x2  
3
3
Respuestas estudiando el comportamiento de la segunda derivada
x<
< x <
3
3
3
3
2
>
0
0
<
0
0


f ( x)  12x  4
Arriba Inflexion abajo
inflexion

 3
3
  0.44 , f 

Valores importantes f  

 3   0.44
3




El bosquejo del gráfico sería
f ( x)  12x 2  4  4(3x 2  1)  0; x1 
<
x
>0
arriba
Maple nos presenta:
27
x
x 3

f ( x)  0
f ( x)  0 
,
x  
x
3  x2
Luego, f (x)  2
y después de innumerables pasos se llega a
( x  3) 2
24. f ( x ) 
2
2 x( x 2  9)
( x 2  3) 3
Las raíces de la primera derivada o puntos críticos son:
f ( x) 
x1   3 , x3  3
Valores importantes f ( 3)  0,29 , f ( 3)  0.29
El comportamiento gráfico de la primera derivada es:
Las raíces de la segunda derivada son x1  3 , x2  0 , x3  3
Estudiemos el comportamiento de la segunda derivada
2 x( x 2  9)
( x 2  3) 3
concavidad
f ( x) 
x<
-3
<x<
0
<0
0
>0
0
< x
<
<0
arriba
inflexión
abajo
Abajo Inflexión
3
<x
0
>0
inflexión arriba
Valores importantes: f (3)  0.25 , f (0)  0 , f (3)  0,25
El gráfico es según Maple
28
25. f ( x ) 
x 1
x 1
Por división se logra que: f ( x ) 
x 1
2
= 1
.
x 1
x 1
Estudiaremos la función f (x) = 1 
2
x 1
2
4
, luego f ( x)  
2
( x  1)
( x  1) 3
La segunda derivada no está definida en x = -1, punto en donde tampoco está
Definida ni la función, ni la segunda derivada.
f ( x) 
Estudiemos la segunda derivada alrededor de x = -1
x <
-1
< x
4
>0
No definida
< 0
f ( x)  
3
( x  1)
La función es cóncava hacia arriba en  ,1 y hacia abajo en (1, )
La primera derivada siempre es positiva lo que indica que la función es creciente,
salvo en el punto de discontinuidad. No hay puntos críticos en el dominio.
Es claro que
f ( x)  1 f ( x)   f ( x)   f ( x)  1
,
,
,
x  1
x  1
x  
x
Todo esto garantiza una asíntota horizontal en y = 1 y una asíntota vertical en
29
x = - 1.
Grosso modo el gráfico sería:
El cual por su excesivo ajuste a los ejes, es presentado por Maple como:
30